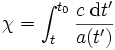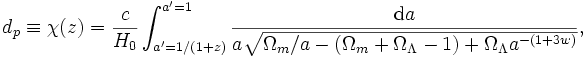Distance comobile - Définition

Introduction

La distance comobile est une caractérisation de la distance séparant deux objets astronomiques en faisant abstraction de l'expansion de l'univers, c'est-à-dire en utilisant une unité de longueur qui suit l'expansion de l'univers.

Tandis que la relativité restreinte dit que tout cadre inertiel de référence est équivalent, c'est-à-dire qu'il n'existe pas de choix « favorisé » de coordonnées de l'espace-temps, celle-ci n'est qu'une théorie locale, valable dans la limite vers un point.

La relativité générale est une théorie locale aussi, mais comme elle modélise la gravité, ce qui manque dans la relativité restreinte, elle est utilisable pour contraindre les propriétés locales d'un espace, appelé formellement une variété riemannienne, de façon à lier ensemble la géométrie locale et la densité. La variété elle-même est globale.

Dans le contexte de la relativité générale, la supposition du postulat de Weyl est qu'un cadre de référence favorisé de l'espace-temps peut être défini et avoir un sens physique. La notion la plus courante qui permet à implémenter cette notion est celle de coordonnées comobiles, où le cadre de référence spatial est attaché aux positions (spatiales) moyennes des galaxies (ou de n'importe quel gros morceau de matière qui se déplace plutôt lentement).

Dans ce choix de coordonnées, l'on peut ignorer à la fois le temps et l'expansion de l'Univers pour se concentrer sur la forme de l'espace (ou plus formellement, d'une hypersurface spatiale à temps cosmologique constant).

L'espace dans les coordonnées comobiles est (en moyenne) statique. Ceci est parfaitement cohérent avec le fait que l'Univers s'étend. Un choix de coordonnées n'est qu'un choix d'étiquettes numériques. Il arrive que, selon le modèle standard du Big Bang, un certain choix pour coller ces étiquettes existe tel qu'il est très pratique et pour les calculs formels, et pour penser de l'Univers comme objet statique. Pour revenir à l'expansion très réelle de celui-ci, il suffit de se rappeler le facteur d'échelle.

Ainsi, il y a aussi le temps cosmologique qui, pour l'observateur sur un point spatial fixe en coordonnées comobiles est identique à sa mesure locale du temps.

La distance comobile est donc la distance en coordonnées comobiles entre deux points dans l'espace, au même point du temps cosmologique :

où a(t') est le facteur d'échelle. Il faudrait éviter ici un mot comme simultanément, parce que tout en ayant un sens global, le temps cosmologique n'est pas identique au temps.

Mots équivalents

• Certains livres utilisent le symbole χ pour la distance comobile.

• Weinberg (1972) utilise le terme distance propre [1] pour la distance comobile.

Autres distances utiles dans la cosmologie

• La distance suivant-le-voyage-du-photon - c'est la vitesse de la lumière multipliée par l'intervalle en temps cosmologique, c.a.d. , tandis que la distance comobile est où a(t) est le facteur d'échelle.
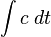
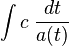
• d_L distance de luminosité
• d_pm distance de mouvement propre, qui est la longueur en coordonnées comobiles correspondant à un angle d'un radian
  • (parfois appelée la distance de taille angulaire par James Peebles 1993 [2])
  • parfois appelée la distance des coordonnées
  • parfois d_pm est appelée la distance de diamètre angulaire
• d_a distance de diamètre angulaire

Les trois dernières sont liées par :

d_a = d_pm / (1 + z) = d_L /(1 + z)²

où z est le décalage vers le rouge.

Si et seulement si la courbure est nulle, alors la distance de mouvement propre et la distance comobiles sont identiques, c.a.d. d_pm = χ.

Pour une courbure négative,

,

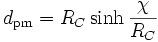
tandis que pour une courbure positive,

,

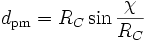
où R_C est la (valeur absolue) du rayon de courbure.

Pour numériquement intégrer d_p de l'observateur jusqu'à un décalage vers le rouge z pour des valeurs arbitraires du paramètre de densité de la matière Ω_m, de la constante cosmologique Ω_Λ, et du paramètre de la quintessence w est

où c est la vitesse de la lumière et H₀ est la constante de Hubble.

En utilisant des fonctions sin et sinh, la distance de mouvement propre d_pm peut être obtenue de d_p.