Énergie potentielle gravitationnelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique classique, l'énergie potentielle gravitationnelle correspond à une forme d'énergie associée au champ gravitationnel. Son interprétation la plus naturelle est liée au travail qu'il faut fournir pour déplacer un objet plongé dans un champ gravitationnel. Plus précisément, la variation d'énergie potentielle gravitationnelle d'une masse se déplaçant entre deux points est l'opposé du travail nécessaire pour déplacer cette masse entre ces deux points quand ceux-ci sont plongés dans une région où règne un champ gravitationnel.
Considérations générales
L'énergie potentielle gravitationnelle est, comme toutes les formes d'énergie potentielle, définie à une constante additive arbitraire près. Néanmoins, il est d'usage de fixer la valeur de la constante en prenant la valeur de l'énergie potentielle nulle lorsque la masse est infiniment éloignée du centre de gravité du champ auquel elle est soumise. Dans ce cas-là, l'énergie potentielle gravitationnelle est négative. Cela signifie qu'il faut fournir un travail positif (c'est-à-dire dépenser de l'énergie) pour extraire une masse d'un champ gravitationnel. Ceci est une conséquence directe du fait que, dans la Nature, les masses sont des quantités positives, qui s'attirent toujours. Ainsi, éloigner une masse d'une distribution arbitraire de masses nécessite de dépenser de l'énergie pour s'opposer à la force attractive entre les différentes masses.
Cas d'une distribution générique de masse
Dans le cas le plus général d'une distribution continue de matière décrite par une densité de masse ρ(r), où r représente le rayon vecteur d'un point quelconque de l'espace, l'énergie potentielle gravitationnelle du système est donnée par la somme de tous les travaux nécessaires pour amener chacune de ses parties depuis l'infini jusqu'à leur position finale. Cette énergie s'écrit alors
-
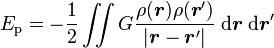
Le facteur 1/2 peut se comprendre par le fait que l'on considère l'ensemble des énergie potentielles prises entre deux points de la distribution de masse, chaque paire de points étant comptée deux fois d'où la nécessité de rajouter un facteur 1/2 dans le résultat final.
Autre écriture
En fonction du potentiel gravitationnel
Du fait que la formule générale du potentiel gravitationnel s'écrit
-
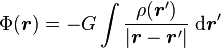
on peut effectuer une des deux intégrations dans la formule précédente, pour obtenir
-
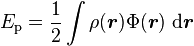
En fonction du champ gravitationnel
Si l'on connaît le champ gravitationnel g généré par la distribution des sources, on peut réexprimer la formule précédente selon
-
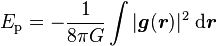
En effet, on peut exprimer le potentiel Φ en un point en fonction de la densité de matière, selon l'équation de Poisson, à savoir
- ΔΦ = 4πGρ.
Ainsi, l'expression de départ se réécrit-elle
-
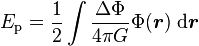
Cette expression peut naturellement s'intégrer par parties, pour donner
-
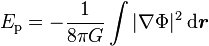
Or le champ gravitationnel n'est rien d'autre que l'opposé du gradient du potentiel Φ. Ainsi,
-
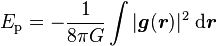
Cette expression est essentiellement similaires aux énergies électrostatique et magnétostatique, faisant l'une et l'autre intervenir l'intégrale sur tout l'espace du carré de la norme du champ correspondant (électrique et magnétique, respectivement), le tout multiplié par la constante appropriée. Par exemple, la constante est ε/2 pour l'énergie potentielle électrostatique et -1/8πG pour l'énergie potentielle gravitationnelle, car les forces électrostatiques et gravitationnelles font intervenir les constantes 1/4πε et G, et que l'une est répulsive pour des charges de même signe, alors que l'autre est attractive.
Cette expression est assez commode dans le cas du calcul de l'énergie potentielle gravitationnelle d'une distribution de matière à symétrie sphérique.