Énergie potentielle gravitationnelle - Définition
La liste des auteurs de cet article est disponible ici.
Expression pour une masse ponctuelle
Considérant une masse m, supposée dans un premier temps ponctuelle, placée en un point dont le rayon vecteur est noté r, si on appelle Φ le potentiel gravitationnel dans lequel se déplace cette masse, alors, l'énergie potentielle gravitationnelle E de celle-ci vaut
-
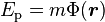
Comme annoncé plus haut, cette énergie est définie à une constante près du fait qu'il en est de même pour le potentiel Φ. Si la distribution des masses à l'origine du potentiel Φ est d'extension limitée, alors il est naturel de choisir une valeur nulle pour le potentiel à l'infini, ce qui donne immédiatement d'après la formule ci-dessus une énergie nulle à l'infini.
Exemples
Satellite en orbite autour de la Terre
Dans le cas d'un satellite artificiel en orbite autour de la Terre que l'on peut en première approximation considérer comme étant à symétrie sphérique, le potentiel dans lequel il est plongé suit la loi suivante :
-
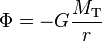
où G est la constante de gravitation, M la masse de la Terre et r la distance par rapport au centre de la Terre. Alors l'énergie potentielle du satellite vaut
-
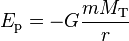
Cette énergie est certes négative, mais supériere à l'énergie potentielle du satellite avant son lancement, puisqu'à ce moment-là, sa distance au centre de la Terre était égal au rayon terrestre, plus petit que sa distance r en orbite.
Sphère homogène
Pour une sphère homogène de rayon R et de masse M, l'énergie potentielle gravitationnelle s'écrit
-
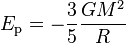
La sphère étant homogène, on peut utiliser le théorème de Gauss pour déterminer le champ en tout point. Ce théorème stipule que le flux sortant du champ au travers d'une shpère centrée sur la distribution de matière est déterminé par la masse interieure à cette sphère. Ainsi, à une distance r du centre, la composante radiale du champ gravitationnel g, notée g, s'écrit
- 4πr2gr = − 4πGM(r),
M(r) étant la masse comprise à l'intérieur du rayon r. Du fait que la distribution de matière est ici supposée homogène à l'intérieur du rayon R, on a
-
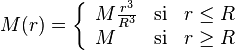
En conséquence,
-
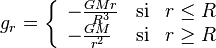
L'intégrale du carré de g à l'intérieur et à l'extérieur de la sphère donne ainsi
-
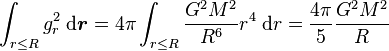
et
-
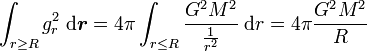
L'énergie potentielle gravitationnelle totale est donc égale à la somme de ces deux quantités, le tout multiplié par -1/8ππG, ce qui donne
Distribution sphérique
D'une manière plus générale, pour une distribution de matière quelconque à symétrie sphérique, l'énergie potentielle gravitationnelle est toujours de la forme
-
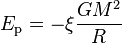
la valeur de la quantité ξ étant déterminée par le détail du profil de densité de la distribution : plus celle-ci est piquée vers le centre, plus cette quantité est grande, ce qui se comprend aisément en remarquant qu'une distribution très piquée de matière est majoritairement confinée dans un rayon notablement plus petit que la rayon total R de la configuration, où ne se situe qu'une petite partie de la masse, qui ne contribue guère au potentiel gravitationnel (ou à l'énergie) totale.
Se fixer un profil de densité revient en réalité à fixer une équation d'état pour la matière considérée. En astrophysique se produisent beaucoup de situations où seule la densité et la pression interviennent, la température étant une quantité inessentielle. L'exemple typique de cette situation est celui d'un polytrope, où pression et densité sont reliées par une loi de puissance du type