Ensemble convexe - Définition

Ensembles convexes et géométrie combinatoire

Les ensembles convexes jouent un rôle central en géométrie combinatoire, ne serait-ce que parce que, face à un nombre fini de points d'un espace affine, l'opération géométrique la plus évidente qu'on puisse leur appliquer est d'examiner leur enveloppe convexe : ce qu'on appelle un polytope.

Polytopes

L'objet de base de la géométrie combinatoire convexe, c'est le polytope, qu'on peut définir comme enveloppe convexe d'un nombre fini de points.

Pour ne citer ici que l'exemple sans doute le plus fameux de résultat de géométrie combinatoire, en dimension 3, les nombres de sommets, d'arêtes et de faces d'un polytope sont liés par la formule d'Euler (voir à ce sujet l'article Caractéristique d'Euler) :

.

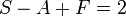
Les théorèmes de Radon, Helly et Carathéodory

Considérons un ensemble de d + 2 points dans un espace affine de dimension d.

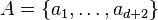
Le théorème de Radon affirme que :

Pour énoncer de façon parallèle les théorèmes de Helly et Carathéodory, on va introduire une notation : pour chaque indice i variant entre 1 et d + 2, notons l'enveloppe convexe des points de A autres que le point a_i. En dimension 2, chaque Δ_i serait un triangle (et il y en aurait quatre) ; en dimension 3 on aurait affaire à une collection de cinq tétraèdres, et ainsi de suite.

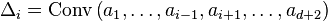
Les deux énoncés suivants sont des cas particuliers des énoncés les plus courants des théorèmes de Helly et Carathéodory, mais qui en contiennent essentiellement toute l'information : on reconstitue facilement les énoncés généraux à partir des versions fournies ci-dessous.

Ces théorèmes sont étroitement liés : la démonstration la plus courante de Helly est fondée sur Radon, tandis qu'on prouve facilement Carathéodory indépendamment, mais il est aussi possible par exemple de déduire Helly de Carathéodory ou le contraire.

D'innombrables variantes les précisent ou les généralisent.