Ensemble convexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
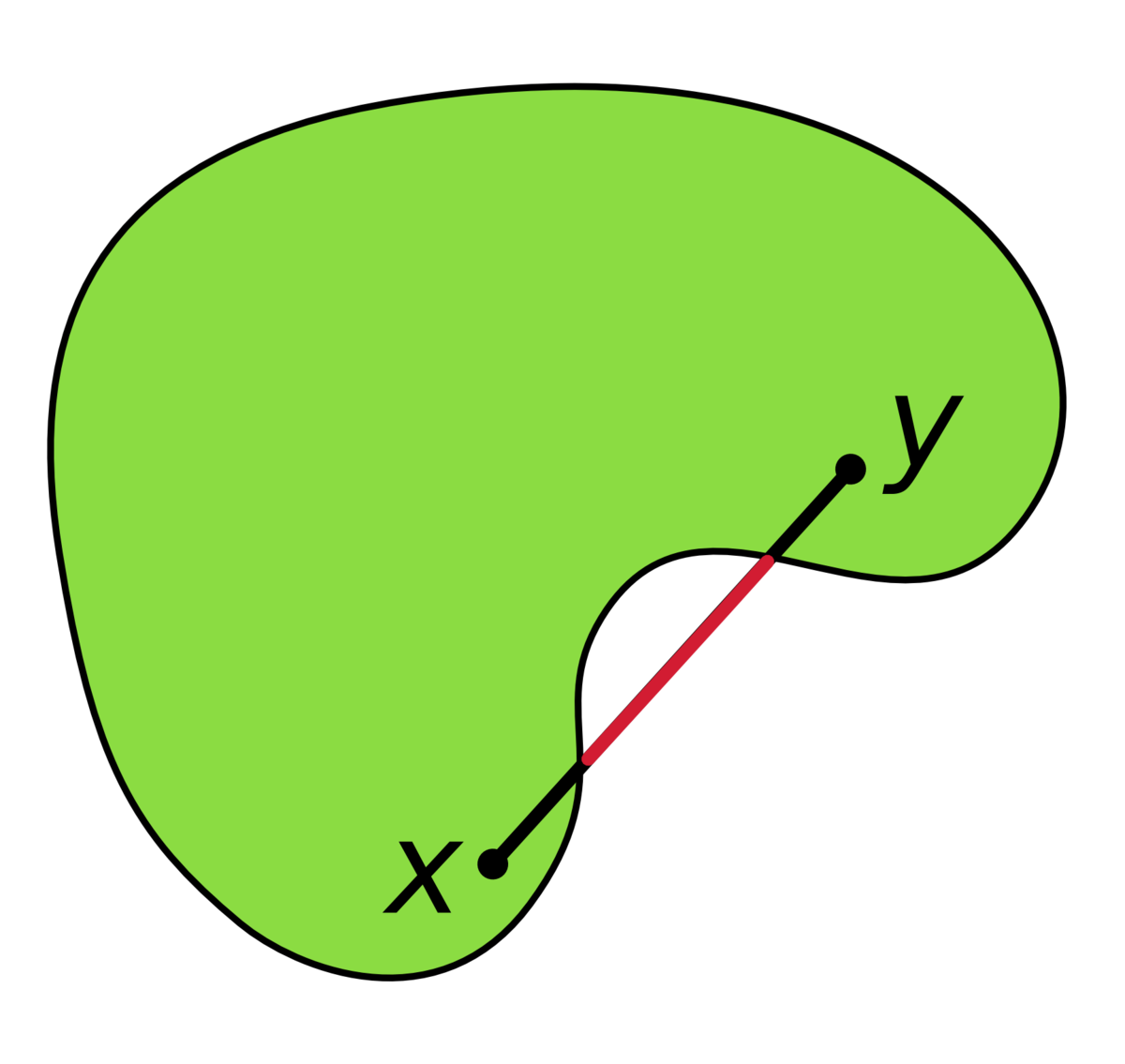
Un objet géométrique est dit convexe lorsque, chaque fois qu'on y prend deux points A et B, le segment [A,B] qui les joint y est entièrement contenu. Ainsi un cube plein, un disque ou une boule sont convexes, mais un objet creux ou bosselé ne l'est pas.
Définition
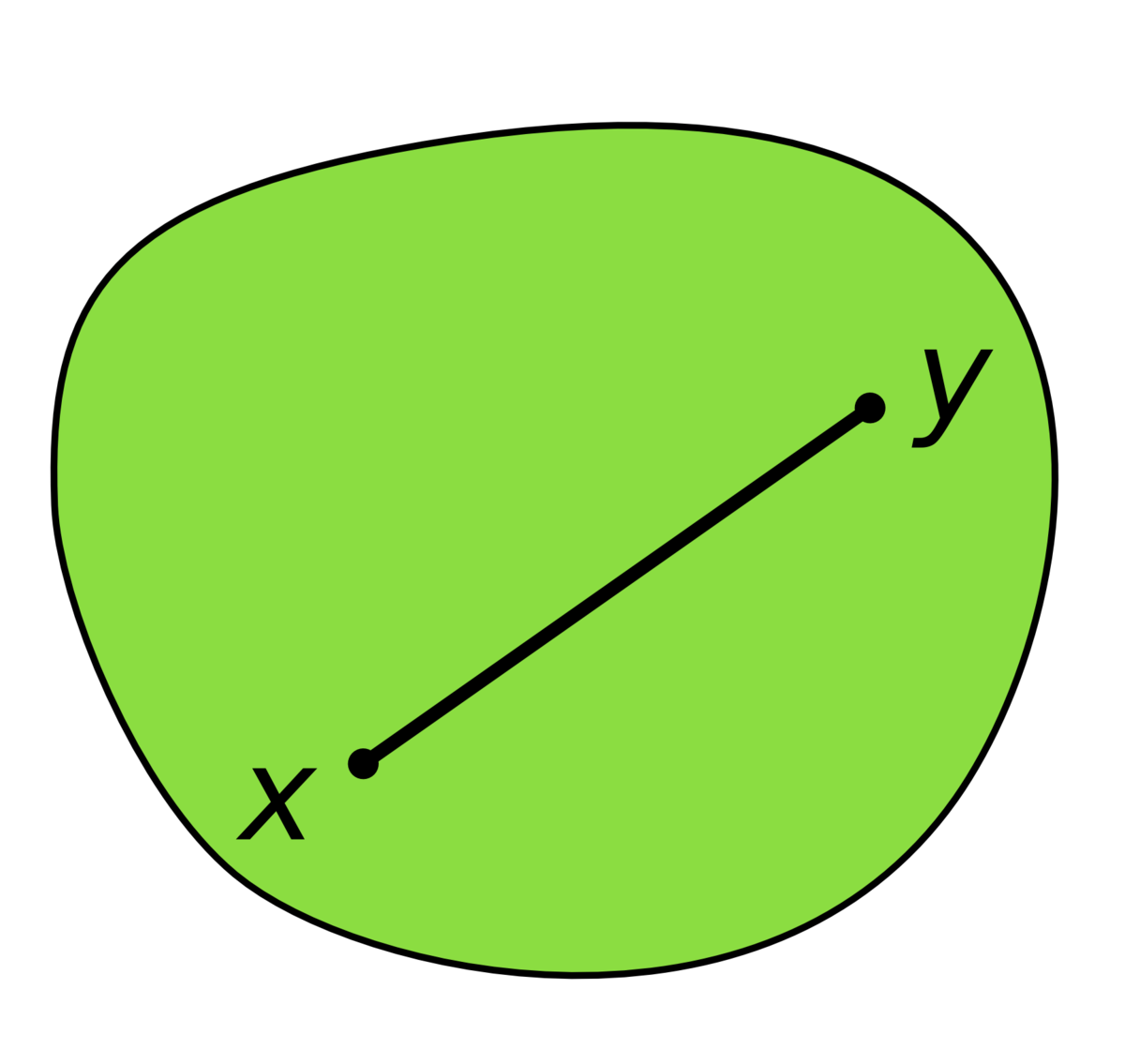
On suppose travailler dans un contexte où le segment [x,y] reliant deux points quelconques x et y a un sens (par exemple dans un espace affine sur

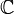
Définition — Un ensemble C est dit convexe lorsque, pour tout x et y de C, le segment [x,y] est tout entier contenu dans C.
Sauf précision explicite, tout ce qui suit concerne le seul contexte des convexes dans des espaces affines (ou vectoriels).
On appellera dimension du convexe non vide C la dimension du sous-espace affine engendré par C.
Exemples
- Les sous-ensembles convexes de

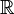
- Dans un espace affine, tout sous-espace affine est convexe ; c'est en particulier le cas des sous-espaces vectoriels des espaces vectoriels.
- Dans un espace vectoriel normé (réel ou complexe), toute boule est convexe, qu'il s'agisse d'une boule ouverte ou d'une boule fermée.
Propriétés topologiques
Dans cette section, on suppose l'espace ambiant muni d'une topologie compatible avec sa structure géométrique (c'est toujours le cas dans les espaces de dimension finie ; si on est dans un espace vectoriel de dimension infinie cela revient à exiger qu'il s'agisse d'un espace vectoriel topologique).
Adhérence, intérieur, frontière
Les opérateurs d'adhérence et d'intérieur préservent la convexité. En outre, lorsque le convexe considéré n'est pas d'intérieur vide (et on peut facilement se ramener à ce cas en le considérant comme partie de son enveloppe affine et non de l'espace global), le convexe, son intérieur et son adhérence ont tous trois la même frontière.
On peut montrer très facilement qu'un convexe compact est l'enveloppe convexe de sa frontière (hors le cas dégénéré de la dimension 0).
Connexité
Une partie convexe est évidemment connexe par arcs donc connexe.
Description à homéomorphisme près en dimension finie
Pour
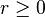
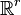
Les compacts convexes disposent d'une structure simple :
Théorème — Soit C un convexe compact de
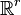
Les convexes fermés d'une dimension finie d donnée sont homéomorphes à l'un ou l'autre d'un nombre limité (d + 2) de modèles simples.
Théorème — Soit
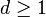
- soit il existe r avec
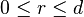
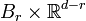
- soit C est homéomorphe à un demi-espace fermé dans
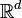
Dans tous les cas, l'homéomorphisme envoie la frontière relative de C sur la frontière relative du modèle.
Pour lire ce théorème sur un exemple instructif, celui de la dimension 3, les convexes fermés de dimension 3 sont homéomorphes à un des cinq modèles suivants :
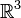
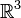
Les intérieurs relatifs de tous les modèles énumérés au théorème précédent sont homéomorphes entre eux, c'est-à-dire homémorphes à
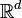
Théorème — Soit
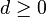
C est difféomorphe à
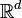
Il ne faut pas espérer une classification aussi simple des convexes sans condition topologique : qu'on songe que pour toute partie A du cercle-unité de
-
- Il existe un entier d tel que le convexe compact C de Rr soit homéomorphe à la boule fermée Bd :
Une translation est un homéomorphisme, il suffit de montrer la proposition pour un translaté de C. On peut donc supposer, sans perte de généralité que C contienne le vecteur nul. Soit F le sous-espace vectoriel de Rn engendré par C.
-
-
- Le convexe C, considéré comme un sous-ensemble de F, est d'intérieur non nul.
-
- Comme, pour un espace vectoriel réel de dimension finie, toutes les normes sont équivalentes, on peut choisir celle pour laquelle la démonstration est la plus simple. Soit (ej) un ensemble de vecteurs de C définissant une base de F. On choisit pour norme, celle qui à un vecteur associe la valeur absolue de sa plus grande coordonnée dans la base (ej). Pour cette norme on remarque que la boule de centre 1/(2d) (Σej) et de rayon 1/2d est formé des vecteurs ayant des coordonnées positives et inférieures à 1/d dans la base (ej). Ces vecteurs sont tous des éléments de C. Ce qui montre que le centre de la boule est bien dans l'intérieur recherché.
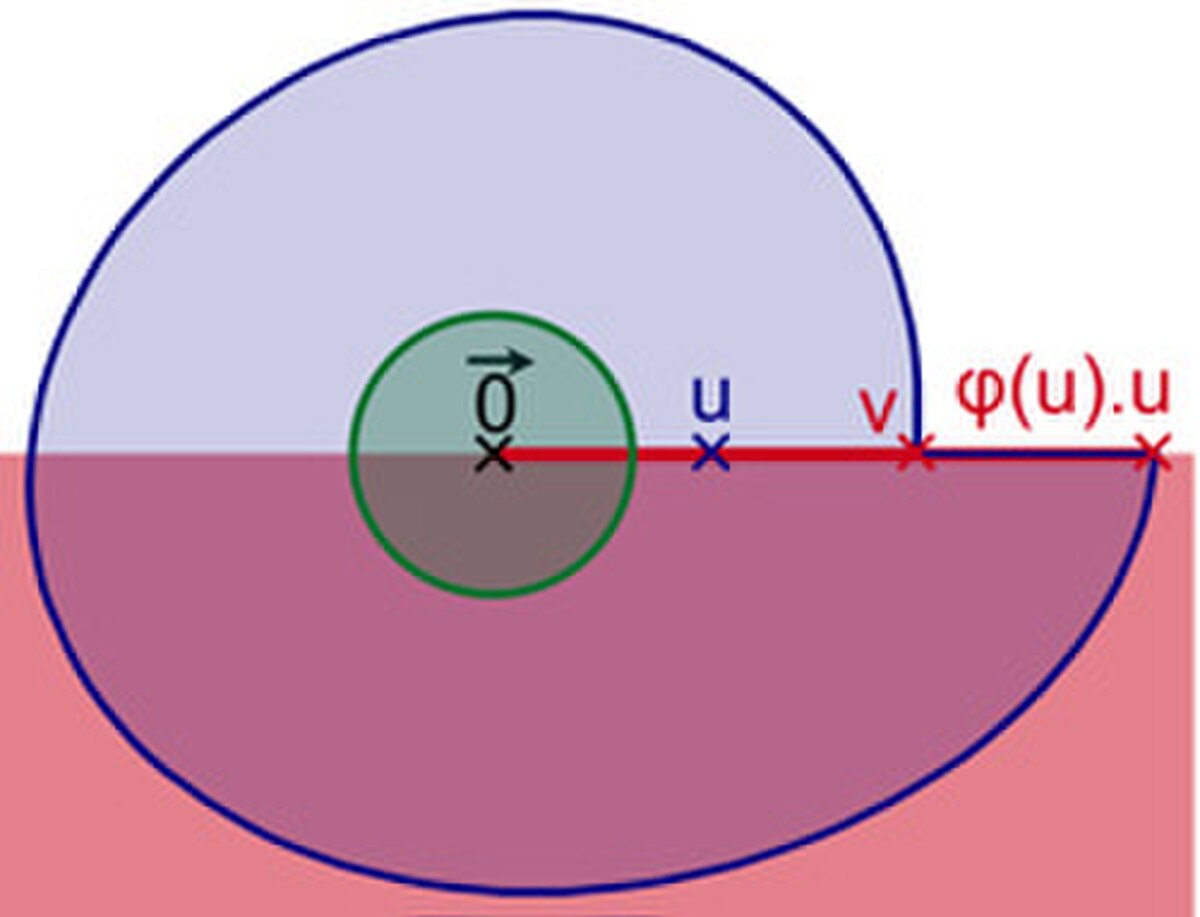
On considère maintenant uniquement l'espace vectoriel F et on note d sa dimension. Quitte à opérer une nouvelle translation, on peut toujours supposer que le vecteur nul est dans l'intérieur de C. On note B la boule fermée de centre le vecteur nul et de rayon 1 et S la sphère de même centre et de même rayon. Soit u un vecteur de S et Eλ(u) l'ensemble des réels positifs λ tels que λu soit élément de C. Comme C est compact, l'ensemble est borné et l'ensemble Eλ(u) l'est aussi. Soit φ(u) la borne supérieure de Eλ(u). On vient de définir une application de S dans R+ qui à u associe φ(u). Comme il existe un voisinage du vecteur nul inclus dans C, la fonction φ ne s'approche jamais de la valeur 0.
-
-
- L'application φ est continue.
-
- Supposons qu'il existe un point u de S tel que φ ne soit pas continue en u. Il existe alors un réel strictement positif μ strictement plus petit que φ(u) tel que :

- La suite (φ(un) est positive et bornée, elle est à valeurs dans un compact et il existe une sous-suite convergente (φ(uψ(n)), d'après le théorème de Bolzano-Weierstrass. Soit λl la limite de cette suite. La suite (φ(uψ(n)).uψ(n)) est une suite de points de la frontière de C, convergeant vers λl.u. Le point v = λl.u est un point de la frontière de C et la distance entre les deux points de la frontière de C φ(u).u et v est supérieur à μ. Comme φ(u) est la plus grande valeur telle que φ(u).u soit un élément de C, λl est strictement plus petit que φ(u) et par construction il est strictement plus grand que 0. Il ne peut valoir 0 car le vecteur nul n'est pas un point de la frontière de C et λl.u l'est. Comme v est un point qui n'est pas dans l'intérieur de C, Il existe un hyperplan d'appui passant par v séparant l'espace en deux composantes connexes, dont l'une contient l'intérieur du compact C (en rouge sur la figure de droite). Cet hyperplan contient la droite passant par le vecteur nul, v et φ(u).u. Cet hyperplan possède une intersection non vide avec le voisinage du vecteur nul strictement inclus dans C (en vert sur la figure). Cette contradiction montre que la fonction φ est continue.
La proposition précédente permet simplement de démontrer le résultat du paragraphe.
-
-
- Le convexe compact C est homéomorphe à la boule B.
-
- On considère l'application de B dans C, qui à u associe φ(u).u, si u est différent du vecteur nul et qui laisse invariant le vecteur nul. Cette application est continue pour tout vecteur non nul. Comme l'application φ est borné (car C est un compact) elle est aussi continue au vecteur nul. L'application φ est bijective. Comme φ(u) n'est jamais nul (si u ne l'est pas), l'application inverse est celle qui, à u différent du vecteur nul, associe φ(u)-1.u et au vecteur nul encore le vecteur nul. L'application considérée est bien un homéomorphisme, ce qui termine la démonstration.