Ensemble convexe - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés élémentaires et outils fondamentaux
Intersections de convexes
L'intersection de deux convexes (et même d'une famille quelconque de convexes) est elle-même convexe (et ce très généralement, dès lors qu'on peut définir la convexité).
Stabilité par barycentres à coefficients positifs
La définition de la convexité fait intervenir le choix de deux points quelconques x et y, puis la considération des points du segment [x,y], autrement dit des barycentres à coefficients positifs de ces deux points. En utilisant le théorème d'associativité des barycentres, on voit sans mal que cela n'aurait rien changé de considérer des barycentres à coefficients positifs d'un nombre quelconque de points. Précisément on a :
Proposition — Un sous-ensemble C d'un espace affine E est convexe si et seulement si pour toute famille finie (x1,...,xk) de points de C et tout choix (λ1,...,λk) de coefficients positifs, le barycentre des (xi) affublés des poids (λi) est lui-même dans C.
Enveloppe convexe
Étant donnée une partie quelconque A de l'espace ambiant E (espace affine ou contexte plus général), il existe au moins un sous-ensemble convexe de E contenant A, à savoir E lui-même ; ceci autorise à considérer l'intersection de tous les sous-ensembles convexes de E contenant A. On l'appelle l'enveloppe convexe de A.
On vérifie aussitôt que c'est donc le plus petit sous-ensemble convexe de E contenant A, au sens de l'inclusion sur P(E). Si x et y sont deux points de E, l'enveloppe convexe de l'ensemble {x,y} est le segment [x,y].
Le théorème de la projection
À condition d'être en train de travailler dans un espace euclidien (ou plus généralement dans un espace de Hilbert), on dispose d'un résultat remarquable : étant donné un convexe fermé, pour tout point x de l'espace, il existe un et un seul point p(x) du convexe à distance minimale de x. Ce résultat est accompagné de diverses informations complémentaires, notamment le caractère obtus de l'angle
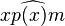
Séparation des convexes et structure de la frontière
Une technique utile est celle de la « séparation » de deux convexes. Elle consiste, étant donné deux convexes sans point commun d'un même espace, à découper cet espace en deux par un hyperplan (un plan en dimension 3) qui laisse les convexes de part et d'autre de ce mur de séparation. Les démonstrations de la possibilité d'un tel découpage sont multiples, permettant d'obtenir des énoncés plus ou moins généraux ; certaines utilisent le théorème de Hahn-Banach, outil d'analyse fonctionnelle particulièrement pertinent pour l'étude en dimension infinie.
Cette méthode permet tout particulièrement de justifier de l'existence en chaque point de la frontière d'un convexe d'un « hyperplan d'appui » : un hyperplan passant par ce point et laissant le convexe tout entier dans l'un des deux demi-espaces qu'il borde. Ce résultat est à son tour fondamental pour étudier plus en détail la structure de la frontière des convexes (divisions en faces, arêtes, etc...) et particulièrement des polyèdres convexes. On est ainsi amenés à distinguer diverses catégories de points (points extrémaux, sommets) qui joueront un rôle central dans les problèmes d'optimisation sur le convexe, par exemple en programmation linéaire.
Fonctions convexes associées à un ensemble convexe
L'étude des ensembles convexes peut bénéficier des résultats d'analyse qui concernent les fonction convexes. Plusieurs telles fonctions peuvent en effet être associées à un convexe non vide C.
- La plus simple est sa fonction indicatrice, variante de la fonction caractéristique adaptée à la convexité : c'est la fonction qui prend la valeur 0 sur C, et la valeur
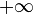
- Lorsque l'espace ambiant est un espace vectoriel de dimension finie, muni d'une structure euclidienne, on peut ensuite considérer la fonction convexe conjuguée de la précédente, qu'on appelle alors la fonction d'appui de C ;

















































