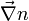Équation eikonale - Définition

Introduction

En optique géométrique, l'équation eikonale ou iconale, est l'équation fondamentale régissant le trajet de la lumière dans un milieu. Elle permet de démontrer toutes les autres lois, telles que les lois de Snell-Descartes et de déterminer les trajectoires des rayons lumineux.

Onde électromagnétique progressive dans un milieu inhomogène

Position du problème

Dans un milieu linéaire local isotrope, mais inhomogène, les composantes spectrales des champs sont données par les équations de Maxwell ; sans sources libres, tous les champs pourront être écrits sous la même forme que le champ électrique :

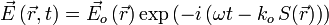
où .

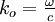
Pour un champ monochromatique donné, il y a une infinité de couples possibles. Dorénavant, on ne considère plus que celui tel que la variation de soit la plus faible à l'échelle de la longueur d'onde λ_o ; la fonction S correspondante est appelée fonction eikonale (ou iconale).

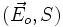
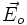
Approximation fondamentale de l'optique géométrique

L'approximation fondamentale de l'optique géométrique consiste à considérer que les variations relatives des amplitudes, ainsi que des constantes et μ_r du milieu, sont très faibles à l'échelle de la longueur d'onde :

.

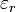
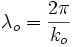
Une analyse d'ordres de grandeur montre que, dans chaque premier membre des équations de Maxwell, le terme comportant k_ogradS est prépondérant, et l'autre négligeable. On en déduit alors facilement la structure de cette onde monochromatique, appelée Onde de l'optique géométrique : les champs sont transverses :

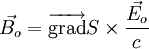
La relation de dispersion est remplacée par l'équation de l'eikonale:

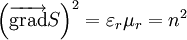
qui s'écrit encore

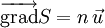
où désigne un vecteur unitaire de .

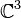
Cette équation ne fait intervenir ni ni ω explicitement ce qui permet de l'atteindre par l'intermédiaire du chemin optique

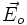
La structure locale de cette onde est analogue à celle d'une onde plane progressive, puisqu'à l'échelle de la longueur d'onde sa phase s'écrit

Soit

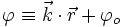
d'où découle la simplicité de l'onde de l'optique géométrique, les manipulations mathématiques effectuées étant les mêmes que pour les ondes planes monochromatiques progressives.

Remarques :

• l'équation de l'eikonale reste valable dans les milieux anisotropes, désignant alors la normale aux ondes en un point, et n est l'un des deux indices possibles en ce point, compte-tenu de la direction de .
• le champ électrique s'écrivant alors en général avec

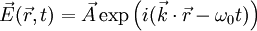
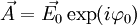
Propagation de l'énergie – Notion de rayon lumineux

Pour des raisons expérimentales, on ne s'intéresse en optique qu'au flux d'énergie moyen, calculé à l'aide d'un vecteur de Poynting moyen . Les rayons lumineux sont définis comme étant les lignes du champ , c'est-à-dire les lignes de courant de l'énergie électromagnétique en moyenne. Si , ou si est réel mais n imaginaire pur, on dit que l'onde est inhomogène (ou évanescente si  ; dans ce cas, n'est parallèle ni à , ni à où , ni au plan avec – mais pour fixé sa direction dépend aussi de donc de la polarisation de l'onde inhomogène. En revanche, si est réel en tout point, l'onde est dite homogène, et alors est parallèle à , indépendamment de  : c'est le miracle de l'optique géométrique : les rayons lumineux sont des lignes du champ (ou ) et ne dépendent pas des caractéristiques ondulatoires ( et ω). Pour toute la suite, on considèrera que est réel partout ; on montre que ceci ne peut être réalisé, en général, que si n est réel en tout point.

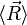
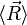
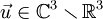
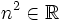
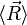
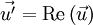
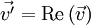
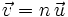
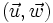
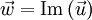
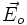
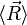
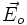
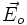
Equation des rayons lumineux

On paramètre le rayon par l'abscisse curviligne s, un point du rayon est donc représenté par le vecteur . Par définition, est tangent au rayon :

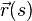
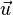
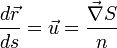
On en déduit l'équation générale d'un rayon lumineux dans un milieu d'indice  :

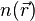
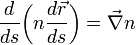
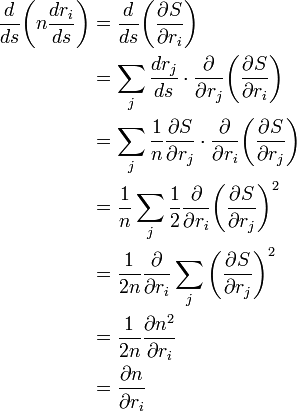
Cette équation permet de décrire le chemin suivi par la lumière dans un milieu homogène (ligne droite), mais aussi lors d'un mirage ou dans une fibre optique par exemple. A la traversée d'un dioptre, diverge, il faut alors utiliser les lois de Snell-Descartes.