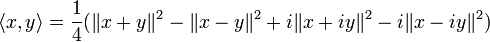Espace hermitien - Définition

Introduction

En mathématiques, un espace hermitien est un espace vectoriel sur le corps des complexes de dimension finie et muni d'un produit scalaire. La géométrie d'un tel espace est analogue à celle d'un espace euclidien. De nombreuses propriétés sont communes aux deux structures.

Ainsi les majorations caractéristiques comme l'inégalité de Cauchy-Schwarz et l'inégalité triangulaire sont toujours valables, l'existence de bases particulières, dites orthonormales, est assurée et la relation canonique entre l'espace et son dual est de même nature que celle de la configuration euclidienne.

Le caractère algébriquement clos du corps sous-jacent rend la diagonalisation des endomorphismes compatibles avec le produit scalaire plus générale. Le terme compatible signifie ici normal, c'est-à-dire commutant avec son adjoint.

Enfin, un espace hermitien de dimension n est aussi un espace euclidien de dimension 2n, en conséquence les propriétés topologiques sont exactement les mêmes.

Cette structure doit son nom au mathématicien français Charles Hermite .

Définition et premières propriétés

Définitions

L'objectif est de généraliser la structure d'espace euclidien aux nombres complexes, qui offre l'avantage d'être un corps algébriquement clos. En contrepartie, il n'existe plus de relation d'ordre compatible avec les opérations du corps, et le carré d'un complexe est parfois négatif. Pour pallier cette difficulté, le produit scalaire n'est plus une forme bilinéaire mais une forme hermitienne.

Une forme hermitienne est une application définie sur ExE à valeur dans notée <.,.>, telle que :

• pour tout y fixé l'application est -linéaire et
• .

En particulier, < x,x > est réel, et est une forme quadratique sur E vu comme espace vectoriel.

Notons aussi qu'une forme hermitienne avec cette définition est sesquilinéaire à droite.

Ce qui amène les définitions suivantes :

Dans ces conditions, la partie réelle de < x,y > est un produit scalaire euclidien pour la structure d'espace vectoriel réel obtenu par restriction, et la partie imaginaire une forme bilinéaire alternée de rang maximum, autrement dit une forme symplectique.

Le terme produit hermitien est synonyme de produit scalaire sur un espace vectoriel complexe.

La donnée du produit scalaire permet de définir une norme et une distance :

Dans toute la suite de l'article E désigne un espace vectoriel complexe de dimension n, C le corps des nombres complexes, <.,.> un produit scalaire, choisi linéaire par rapport à la première variable et semi-linéaire par rapport à la seconde. La norme est notée .

Exemples

• L'espace vectoriel Cⁿ, muni du produit scalaire canonique

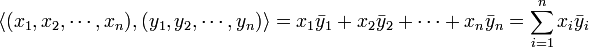
est un espace hermitien appelé espace hermitien canonique de dimension n.

• L'espace vectoriel des polynômes complexes de degré inférieur ou égal à n,

• muni du produit scalaire canonique :

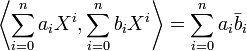
est un espace hermitien de dimension n + 1.

• muni du produit scalaire :

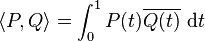
est aussi un espace hermitien dont la norme et la distance associées sont différentes de la précédente. Ce produit scalaire est plus généralement défini sur l'espace des polynômes complexes, sans condition de degré (espace de dimension infinie).

• muni du produit scalaire :

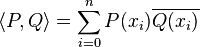
(où x₀, ... x_n sont n + 1 complexes distincts) est aussi un espace hermitien dont la norme et la distance associées sont différentes des précédentes.

Inégalités et identités

A l'image de la situation réelle, les deux majorations classiques sont toujours vérifiées. Si x et y désignent deux vecteurs de E :

• L'inégalité de Cauchy-Schwarz :
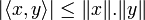
• L'inégalité triangulaire :

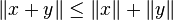
Cette dernière montre que le troisième axiome de la définition d'une norme, dit de sous-additivité est vérifié. Les deux autres (séparation et homogénéité) le sont de manière évidente.

Si R(λ) désigne la partie réelle du nombre complexe λ, le développement du carré de la norme d'une somme :

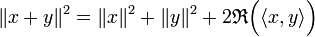
permet d'établir le théorème de Pythagore : si x et y sont orthogonaux, alors

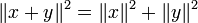
A la différence de la situation euclidienne, la réciproque n'est plus vraie, en effet le carré de la norme somme de deux vecteurs est égal à la somme des carrés des normes si et seulement si la partie réelle du produit scalaire des deux vecteurs est nulle.

• Le développement du carré de la norme de la somme de deux vecteurs montre la règle du parallélogramme :

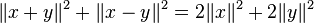
• Ainsi que l'identité polaire :
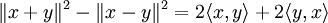
• Elle prend aussi la forme suivante, appelée identité de polarisation :