Flot (mathématiques) - Définition

Comportement asymptotique

Comportement à la limite du domaine

L'équation différentielle x' = -x² n'admet pas de solution sur R tout entier si l'image de 0 n'est pas nulle.

Pour une valeur de x prise dans E, la courbe intégrale maximale t → α_t0(t, x) est parfois définie sur R, mais pas toujours. Deux obstacles peuvent se présenter. Un premier cas est celui où la courbe atteint les limites de l'ouvert Ω. Si tel n'est pas le cas, il n'existe qu'un seul obstacle possible : la courbe n'est pas bornée.

• Soit b la borne supérieure du domaine de définition de la courbe intégrale maximale s vérifiant la condition de Cauchy s(t₀) = x₀, si b est fini et si f est bornée sur le graphe de s au voisinage de b, alors l'ensemble B suivant est d'intersection vide avec Ω .

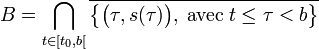
En effet, si f est bornée sur le graphe de s au voisinage de b, alors la solution s admet une dérivée bornée et est uniformément continue sur ce voisinage, ce qui montre que s est uniformément continue sur [t₀, b[ et il est donc possible de la prolonger par continuité sur b. Si (b, s(b)) était élément de Ω, le théorème de Cauchy-Lipschitz montrerait que la solution s se prolonge aussi sur un voisinage de b dans R, autrement dit que b n'est pas la borne supérieure de la courbe intégrale maximale. Par hypothèse b est cette borne supérieure, cette contradiction permet d'en déduire que les valeurs d'adhérences de l'ensemble B ne sont pas dans Ω et termine la démonstration.

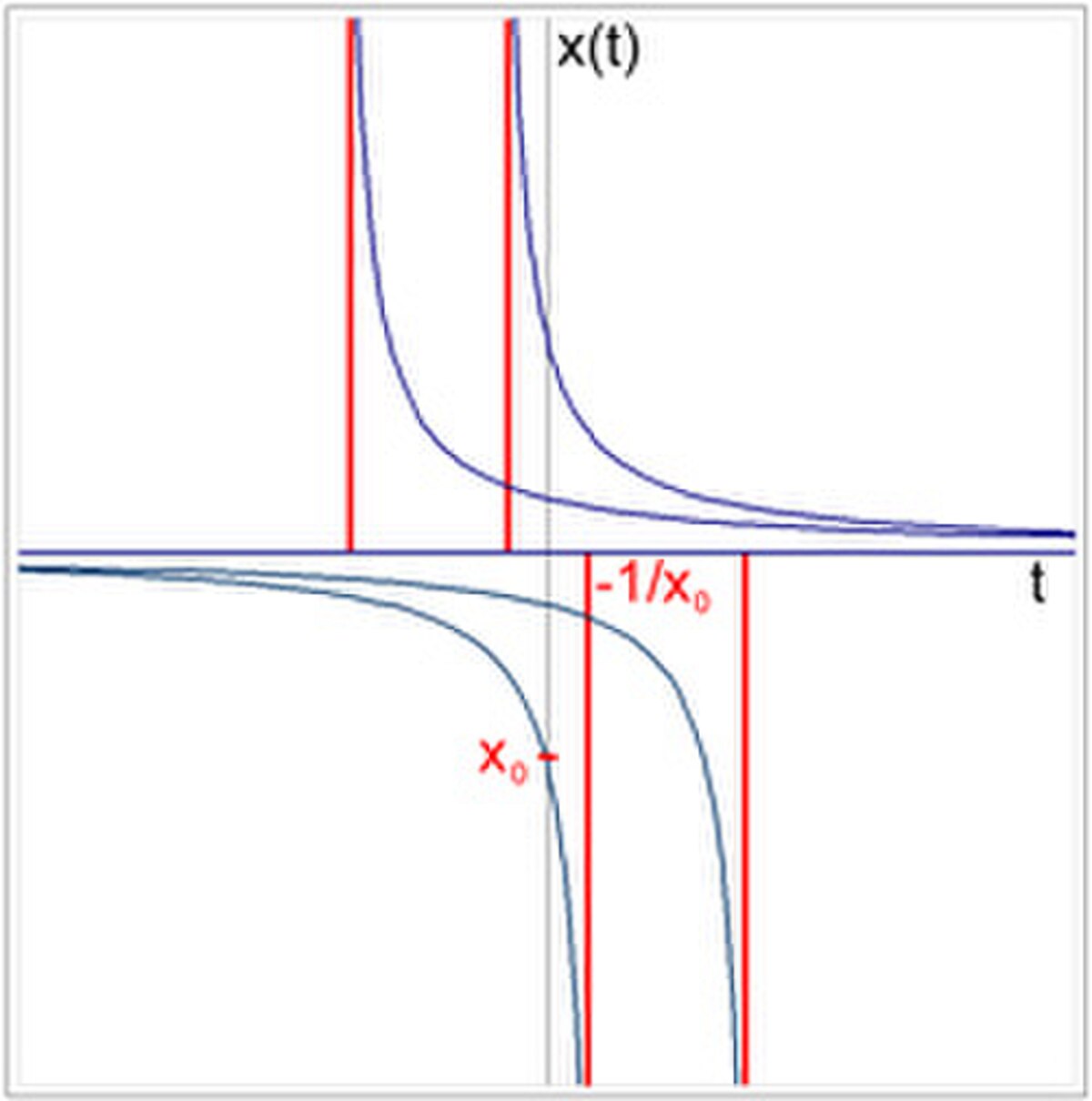
Un exemple est donné par l'équation x' = -x². La solution s'écrit :

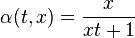
Pour les images de 0 par une courbe intégrale différentes de 0, il n'est pas possible de prolonger les courbes au-delà de -1/x.

Ensemble ω-limite

On suppose ici que l'équation différentielle étudiée est autonome. Une méthode pour étudier le comportement asymptotique est d'analyser l'ensemble ω-limite d'une orbite. Cet ensemble possède toujours les propriétés suivantes :

• Soit x un élément de Ω, l'ensemble ω-limite ω(x) est un fermé invariant par le flot.

En particulier, si y est un point de la trajectoire passant par x, alors ω(x) = ω(y). Si l'orbite ne x n'est pas à valeurs dans un ensemble borné, la proposition peut s'avérer moins forte qu'il n'y parait : l'ensemble ω(x) peut être vide. Tel est le cas si la courbe intégrale s ayant pour condition de Cauchy s(0) = x est définie par s(t) = v.t où v est un vecteur non nul de E. Si l'orbite est compact. On dispose alors des propriétés suivantes :

• Avec les notations précédentes, si la trajectoire de x est à valeurs dans un compact K, ω(x) est un connexe compact non vide.

La trajectoire peut néanmoins être complexe, le système dynamique de Lorenz est un exemple exhibant des ensembles ω-limites compacts dont la dimension de Hausdorff n'est pas égale à 1.

Par définition l'ensemble ω(x) est une intersection de fermés, il est donc fermé. Dans la suite des démonstrations, le flot associé à l'équation différentielle est noté α(t, x).

• Si t est un nombre réel, alors ω(x) = ω(α(t, x)) :

Cette proposition est simple à démontrer, il suffit de comparer les définitions des deux ensembles :

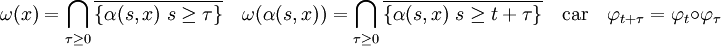
• ω(x) est invariant par l'action du flot α(t, x) :

Cette propriété est encore intuitive, soit y un élément de ω(x), il existe une suite réelle croissante (t_n), de limite plus l'infini, tel que la suite (α(t_n, x)) admette pour limite y. Le flot α de RxK dans K est une fonction continue, donc la suite (α(t, (α(t_n, x))) admet pour limite α(t, y). La structure du groupe du flot montre que la suite s'écrit encore (α(t + t_n, x)) et la suite (t + t_n) est bien une suite croissante de limite plus l'infini.

• ω(x) est un compact non vide :

Montrons dans un premier temps que ω(x) est non vide. Soit on considère la suite (α(t_n, x)), c'est une suite à valeurs dans le compact K. Le théorème de Bolzano-Weierstrass indique que l'on peut en extraire une suite (α(t_φ(n), x)) convergente. Sa limite est par définition dans ω(x).

L'ensemble ω(x) est défini comme une intersection de fermés, c'est un fermé. Il prend ses valeurs dans le compact K, il est donc borné. Dans le plan, tout fermé borné est compact.

• ω(x) est un connexe :

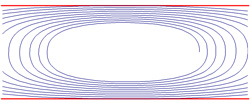
Cette proposition n'est pas nécessairement vraie si ω(x) n'est pas compact. La raison est illustrée sur la figure de droite. Si la trajectoire est une spirale aplatie, dont les côtés s'éloignent à l'infini, l'ensemble ω-limite se réduit à deux droites, illustrés en rouge. Il n'est donc pas connexe.

On suppose ici que ω(x) est non connexe. On va montrer qu'il ne peut être compact. Par contraposé, on obtient la démonstration. On note E_n l'adhérence de l'image de l'intervalle d'extrémités n et l'infini, par la courbe intégrale. Par définition, l'intersection des E_n est égal à ω(x) et les E_n forment une suite de fermés emboités. Par hypothèse, ω(x) n'est pas connexe et il existe deux ouverts disjoints et non vides dont l'union est égale à ω(x). Soit O l'union de ces deux ouverts. Le complémentaire de O dans E_n, noté F_n est un fermé non vide car E_n est connexe (il est défini comme l'adhérence d'un connexe). La suite F_n est une suite de fermés emboités dont l'intersection est vide alors qu'aucun d'eux ne l'est. Aucun compact ne peut contenir une telle suite, ce qui termine la démonstration.

 

Théorème de Poincaré-Bendixson

Il existe un cas où le flot dispose d'un comportement asymptotique relativement simple, il se produit si l'équation différentielle associée est autonome, si l'espace E est le plan et si la courbe intégrale considérée est compact. On dispose alors du théorème suivant, si α est le flot et x un point de Ω.

• Dans le cadre des hypothèses du paragraphe, la fonction qui à t associe α(t, x) est une fonction définie sur R. Si cette fonction n'est pas convergente, l'ensemble ω-limite est l'image d'une orbite cyclique.

Ce théorème se généralise mal. Si E est de dimension supérieure à deux, le système dynamique de Lorenz montre que le résultat du théorème n'est plus généralement vrai.