Flot (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Sensibilité à la condition initiale
Résumé
Dans sa version élémentaire, le théorème de Cauchy-Lipschitz montre l'existence et l'unicité d'une courbe intégrale maximale, cependant aucune information ne concerne la sensibilité à la condition initiale. Il est possible de pallier cette faiblesse :
-
- Le domaine de définition ainsi que le flot global αt0 est unique et il est continu, de classe C1 par rapport à la première variable et localement lipschitzien. Le domaine de définition est ouvert.
-
- Si la fonction f est de classe Cp, il en est de même du flot global αt0.
L'unicité du flot s'entend avec la condition de Cauchy αt0(t0, x) = x pour tout x tel que (t0, x) soit élément du domaine de définition du flot global. Modifier la valeur de t0 correspond à définir un nouveau flot. Cependant ce nouveau flot n'apporte pas d'information supplémentaire, il correspond au précédent, à une translation de la première variable près.
Pour certaines études, comme celles analysant des singularités de courbes intégrales, il est utile d'ajouter un paramètre à l'équation, qui prend la forme : x' = f(t, x, λ). Le flot global dépend alors du paramètre λ, choisi dans un Banach F. La question est celle de la régularité du flot global en fonction du paramètre. Le théorème décrivant cette situation est parfois dénommé théorème de Cauchy-Lipschitz : cas non autonome avec paramètre. Si la fonction f est de classe Cp, le flot, considéré comme une application d'un ouvert de RxExF est aussi de classe Cp.
Continuité du flot local
Dans un premier temps, on étudie le cas de l'équation (1), c'est-à-dire celui d'une équation différentielle autonome. L'objectif est d'établir la continuité locale d'un flot, c'est-à-dire d'analyser ce qui se passe si la condition de Cauchy est peu modifiée. On souhaite définir une fonction β sur un voisinage d'un couple (0, x0), avec x0 élément de Ω, telle que l'application qui à t associe β(t, x) soit une solution de l'équation (1) vérifiant la condition de Cauchy β(t, x) = x.
Soit a un réel strictement positif et B la boule fermée de centre x0 et de rayon a. La valeur a est choisie telle que la boule fermée de centre x0 et de rayon 2.a soit incluse dans Ω et telle que la restriction à cette boule de la fonction f soit k-lipschitzienne, avec k strictement supérieur à 0. Soit m un majorant strictement positif de la norme de f sur la zone considérée, qui existe car f est lipschitzienne sur cette zone. Soit enfin b un réel strictement positif, strictement plus petit que a/m et que m/((1 + m)k). Ce réel b permet de définir un espace de fonctions G sur lequel on construit une application Ψ satisfaisant au théorème du point fixe. Soit G l'ensemble des fonctions définies sur [-b, b]xB, à valeurs dans la boule fermée de centre x0 et de rayon 2.a, continues, m+1-lipschitziennes par rapport à la deuxième variable et telles que l'image d'un point (0, x) soit égal à x, si x est un élément de B.
-
- Lemme 1 : Muni de la norme de la convergence uniforme, G est un espace complet.
On considère une application Ψ, qui à une fonction u de G associe la fonction Ψu, définie par :
![\forall (t,x) \in [-b,b]\times B\quad \Psi_u (t,x) = x + \int_0^t f(u(\tau,x)) \mathrm d \tau](https://static.techno-science.net/illustration/Definitions/autres/0/0b6bd31e5073439d45651994ab2d0b35_9dc9d48431542918984ef1dfebe5d193.png)
Dire qu'une fonction β est un flot sur [-b, b]xB est équivalent à dire que β est un point fixe de Ψ.
-
- Lemme 2 : L'application Ψ est à valeurs dans G et est contractante.
On en déduit l'existence et l'unicité d'un point fixe β c'est-à-dire d'un flot local au voisinage de (0, x). Comme le point fixe est élément de G, il est continu et lipschitzien par rapport à la deuxième variable. Le fait que β soit un point fixe montre que :
![\forall (t,x) \in [-b,b]\times B\quad \beta(t,x) = x + \int_0^t f(\beta(\tau,x)) \mathrm d \tau](https://static.techno-science.net/illustration/Definitions/autres/e/e8e902414a5b419b0c18599c5888fb98_b16d9f20edc44b71307bb3e33d986c6a.png)
Les fonctions f et β étant continues, β est dérivable par rapport à t, ce qui montre que β est lipschitzienne et termine la démonstration de la proposition suivante :
-
- Proposition : Soit x0 un élément de Ω, il existe un voisinage de (0, x0) tel qu'il existe un unique flot local associé à l'équation (1) et défini sur ce voisinage. Ce flot est continu, lipschitzien et dérivable par rapport à la première variable.
-
- Muni de la norme de la convergence uniforme, G est un espace complet :
L'espace des fonctions continues définies sur [-b, b]xB et à valeurs dans la boule fermée de rayon 2.a et de centre x0, muni de la norme de la convergence uniforme, est complet (car l'ensemble d'arrivée des fonctions de cet espace l'est). Il suffit donc de montrer que G est fermé dans cet ensemble, pour la topologie de la convergence uniforme. En fait il l'est déjà pour la topologie de la convergence simple, comme intersection des fermés suivants :
- pour tout point x de B, l'ensemble des fonctions u telles que u(0,x)=x
- pour tout réel t de [-b, b] et toute paire {x,y} de points de B, l'ensemble des fonctions u telles que ||u(t,x)-u(t,y)|| soit inférieur ou égal à (1+m)||x-y||.
-
- L'application Ψ prend ses valeurs dans G :
La majoration suivante permet de conclure que Ψu est bien à valeurs dans la boule fermée de centre x0 et de rayon 2.a, car b est choisi strictement plus petit que a/m :
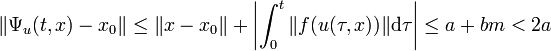
On remarque que l'image de (0, x) par Ψu est bien égal à x. Montrons que Ψu est une application continue, soit (t, x) et (t+δt, x+δx) deux points du domaine de définition de Ψu :
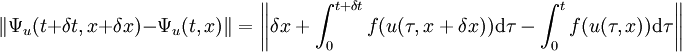
On en déduit :
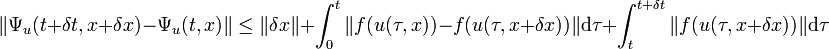
Le deuxième terme de droite est majoré car u est m+1-lipschitzien par rapport à la deuxième variable et f est k lipschitzien. Le troisième terme l'est car f est une fonction bornée par m. Le fait que b soit strictement plus petit que m/(k(m + 1)) montre la majoration suivante
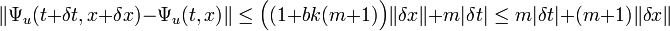
Cette majoration montre que Ψu est une fonction continue. Le caractère lipschitzien par rapport à la deuxième variable se vérifie en choisissant δt égal à 0. On remarque de plus qu'une image par Ψ est aussi lipschitzienne (par rapport aux deux variables).
-
- L'application Ψ est contractante :
Soit u et v deux applications de G, on dispose des majorations :
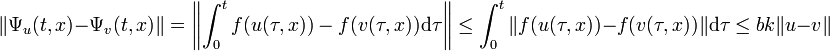
Comme b.k est strictement plus petit que 1, la fonction est bien contractante.
Équation différentielle non autonome
A l'aide d'un habile jeu d'écriture, il est possible de généraliser le cas particulier précédent aux équations dépendantes du temps. On considère maintenant l'équation (2) du théorème, associée à la condition de Cauchy C. Soit g, la fonction de Ω dans le Banach RxE, définie par :
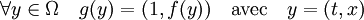
Si y0 désigne le point de Ω égal à (t0, x0), on considère l'équation différentielle et la condition de Cauchy suivante :
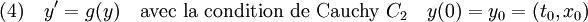
La fonction g est localement lipschitzienne car f l'est. En effet, si y est un élément de Ω, il existe un voisinage V de y et un réel k strictement positif associée à f tel que, si les coordonnées d'un point y1 (resp. y2) de V, sont notées ((t1, x2) (resp. (t2, x2)), on a :
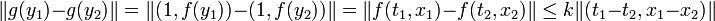
L'équation (4) est bien une équation différentielle autonome, le paragraphe précédent assure l'existence et l'unicité d'un flot local. Soit βg(τ, y) la solution locale de l'équation (4) autour du point y0. On dispose des égalités, si β2 g désigne la deuxième coordonnée de βg :
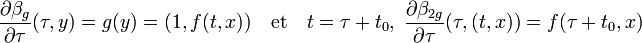
Soit βt0 la fonction qui à (t, x) associe la valeur de la fonction β2 g au point (t - t0, (t0, x)). Les égalités suivantes montrent que β est bien le flot local de l'équation (2), défini sur un voisinage de (t0, x0), et contenant la courbe intégrale locale de l'équation (2) avec la condition de Cauchy C :
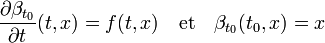
-
- Proposition : Soit (t0, x0) un élément de Ω, il existe un voisinage de (t0, x0) tel qu'il existe un unique flot local associé à l'équation (2) et défini sur ce voisinage. Ce flot est continu, lipschitzien et dérivable par rapport à la première variable.
Équation différentielle avec paramètre
On souhaite maintenant étudier le cas d'un flot local associé à l'équation :
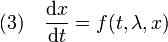
Le paragraphe précédent montre que l'on peut se ramener au cas de l'équation différentielle autonome : x' = f(λ, x). On suppose maintenant que λ est élément d'un Banach F et Ω est un ouvert de FxE et f est une fonction localement lipschitzienne définie sur Ω. Le couple (λ0, x0) est un élément de Ω. La même astuce que celle du paragraphe précédent permet de montrer l'existence locale d'un flot dépendant maintenant de trois variables t, λ et x au voisinage de (0, λ0, x0). Ce flot local est lipschitzien et dérivable par rapport à la première variable. Soit g, la fonction de Ω dans le Banach FxE, définie par :
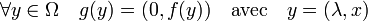
Avec le même raisonnement que le paragraphe précédent, on montre l'existence d'un flot local βg défini au voisinage du point (0, λ0, x0) et à valeurs dans FxE tel que :
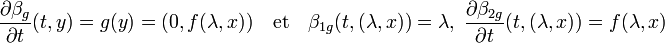
On définit de même le flot β qui à (t, λ, x) associe la valeur de la fonction β2 g au point (t, (λ, x)). Les égalités suivantes montrent que β est bien le flot local de l'équation du paragraphe, défini sur un voisinage de (0, λ0, x0), et contenant la courbe intégrale locale de l'équation considérée, avec la condition de Cauchy (0, x0) :
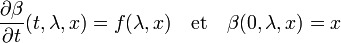
Avec le paragraphe précédent, on en déduit la formulation générale :
-
- Proposition : Soit f une fonction localement lipschitzienne définie sur Ω un ouvert de RxFxE et (t0, λ0, x0) un élément de Ω, il existe un voisinage de (t0, λ0, x0) tel qu'il existe un unique flot local associé à l'équation (3) et défini sur ce voisinage. Ce flot est continu, lipschitzien et dérivable par rapport à la première variable.
Régularité du flot local
Les démonstrations associées à la régularité du flot ont pendant longtemps étés un peu complexes. De manière indépendante Pugh et Robbin ont trouvé une démonstration élémentaire utilisant le théorème des fonctions implicites. Une fois encore, l'équation considérée est celle notée (1), c'est-à-dire que la paragraphe ne traite que d'une équation différentielle autonome. Les deux paragraphes précédents montre que traiter ce cas particulier implique le cas général de l'équation non autonome avec paramètre.
Soit x0 un élément de U, b un réel strictement positif tel qu'il existe un flot local β défini sur l'ensemble [-b, b]xU. Dans ce paragraphe, G désigne le Banach des fonctions continues de [-b, b] à valeurs dans E, la norme du Banach est celle de la convergence uniforme. Enfin, V est le sous-ensemble des fonctions de G dont l'image est incluse dans U. On remarque que V est un ouvert de E. En effet, si f est un élément de G, l'image de f, encore notée f([-b, b]), est un compact inclus dans U, la distance δ de ce compact au complémentaire de U dans E est un réel strictement positif et la boule de centre f et de rayon δ/2 est inclus dans V. Ceci montre que pour tout élément f de V, il existe une boule de centre f et de rayon strictement positif inclus dans V et, par voie de conséquence, que V est ouvert.
On considère l'application Tb de UxV dans G définie par :
![\forall x \in U,\; \forall \sigma \in V,\; \forall t \in [-b,b]\quad T_b(x,\sigma)(t) = x + \int_0^t f(\sigma(\tau))\mathrm d \tau - \sigma(t)](https://static.techno-science.net/illustration/Definitions/autres/b/b8cf97ae74c2d8903d6d3423a974e60e_6629f36393f0c3d298dda29c074bb34a.png)
Dire qu'un couple (x, σ) est un zéro de la fonction Tb revient à dire que σ est une solution locale de l'équation (1) avec la condition de Cauchy σ(0) = x.
On dispose du lemme suivant :
-
- Lemme 1 : Il existe un réel b strictement positif tel que la fonction Tb soit de classe C1 et satisfasse les hypothèses du théorème des fonctions implicites.
Cela signifie que la fonction implicite, donnée par l'équation Tb(x, σ) = 0 est définie localement. Or un élément du graphe de cette fonction implicite possède pour deuxième coordonnée, une solution locale σ de l'équation (1) avec la condition de Cauchy σ(0) = x et définie sur le domaine domaine [-b, b]. Autrement dit, la fonction qui à x associe β(., x) est de classe C1, ce qui permet de déduire un premier résultat :
-
- Lemme 2 : Si la fonction f est de classe C1, le flot local β l'est aussi.
La deuxième différentielle partielle de β vérifie une équation différentielle non autonome. Le paragraphe traitant de ce type d'équation montre qu'elle peut se ramener à une équation autonome, ce qui permet de montrer que la différentielle de β est aussi de classe C1, puis par récurrence, on montre que si f est de classe Cp. Le paragraphe sur les équations différentielles avec paramètres montre que ce résultat se généralise aux équations de type (3) :
-
- Proposition : Si une fonction f définissant une équation différentielle non nécessairement autonome et à paramètre est de classe Cp, il existe un ouvert contenant (t0, λ0, x0) et le flot local défini sur cet ouvert est de classe Cp.
-
- Il existe un réel b strictement positif tel que la fonction Tb soit de classe C1 et satisfasse les hypothèses du théorème des fonctions implicites :
Dans un premier temps, il est nécessaire de montrer que Tb est de classe C1, ce qui est équivalent à montrer que les deux différentielles partielles de Tb, par rapport à x et par rapport à σ, existent et sont continues. La première, D1 (celle par rapport à x) est égale à l'application constante Id où Id désigne l'opérateur identité de E dans E. Montrer l'existence de la deuxième différentielle partielle, revient à montrer la différentiabilité de l'application qui à σ associe une primitive de la fonction t → f(σ(t), car le terme restant est affine par rapport à σ et donc différentiable. L'objectif est de montrer que, si h désigne une application de G :
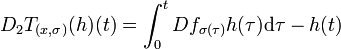
Pour établir cette égalité, calculons une majoration de l'expression Δ, si :
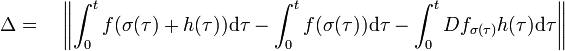
La définition de la différentielle montre l'existence d'une fonction continue εσ(τ)(h(τ)), avec σ(τ) élément de σ([-b, b]), qui vaut 0 si h est égal à 0 et vérifiant l'égalité :
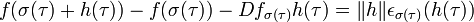
La fonction ε peut être vue comme une fonction à deux variables réelles σ(τ) et h(τ), continue et tel que εσ(τ)(0) soit nul. Il existe un voisinage compact produit de l'intervalle [σ(-b), σ(b)] et d'un voisinage compact de 0 sur lequel la fonction ε est définie et continue. Le fait que εσ(τ)(0) soit nul montre que l'on peut choisir le voisinage de 0 tel que la fonction ε soit bornée par une valeur strictement positive μ arbitrairement petite. Ce qui s'écrit, à l'aide de la continuité uniforme de ε :
![\forall \mu \in \R_+^*,\;\exists \nu \in \R_+^*,\; \forall t \in [-b,b]\quad \|h\| < \nu \Rightarrow \|f(\sigma(\tau) + h(\tau)) - f(\sigma(\tau)) - Df_{\sigma(\tau)}h(\tau)\| < \|h\|\mu](https://static.techno-science.net/illustration/Definitions/autres/c/cee99a10bba3aa0a7f5f351471235f92_7513f1bc51e42fa3a8782a1dcebd9223.png)
On en déduit :
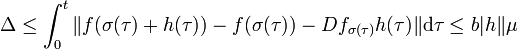
Cette majoration permet le calcul de la deuxième différentielle partielle. En effet :
![\forall \mu \in \R_+^*,\;\exists \nu,\; \forall t \in [-b,b]\in \R_+^*\quad \|h\| < \nu \Rightarrow \left\|T_b(x,\sigma + h)-T_b(x,\sigma) -\int_0^t Df_{\sigma(\tau)}h(\tau) \mathrm d\tau - h(t) \right\| \le b\|h\|\mu](https://static.techno-science.net/illustration/Definitions/autres/4/495c0f4973533c0b98353186d2e84417_7af55f7b6e0f5a37c9cd23300376895e.png)
Ce qui montre l'existence de la deuxième différentielle partielle et donne l'expression :
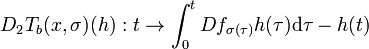
La deuxième différentielle partielle est une fonction indépendante de la première variable x et continue en la deuxième variable σ car l'application f est continument différentiable. La deuxième différentielle partielle est donc aussi continue, comme la première l'est, l'application Tb est bien continument différentiable.
Il reste à montrer que la deuxième différentielle partielle au point x est bijective et que son inverse est continue. La fonction de [-b, b], qui à τ associe Dfσ(τ) est continue et définie sur un compact, elle atteint sa borne supérieure, notée ici C. Ceci montre qu'au point x, D2Tb est la somme de l'opposé de l'identité et d'une application u de norme inférieure ou égale à b.C. Si b est choisi suffisamment petit, la norme de u est inférieure à 1/2. Dans ce cas et au point x, D2Tb, qui est égal à -Id + u, est inversible d'inverse continu car :
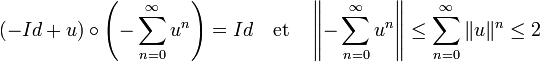
Les deux différentielles partielles de Tb existent et sont continues, ce qui montre que Tb est continument différentiable, si b est choisi suffisamment petit, la deuxième différentielle partielle de Tb est inversible au point x, les hypothèses du théorème des fonctions implicites sont bien réunies.
-
- Si x0 est un élément de U, il existe un voisinage ]-b, b[xUx0 de (0, x0) tel que le flot local β défini sur ce voisinage soit de classe C1 :
Si x0 est un élément de U, le théorème des fonctions implicites indique l'existence d'un voisinage Ux0 de x0 et d'une fonction de classe C1, notée Ψ, de Ux0 dans V tels que l'équivalence suivante soit vérifiée :
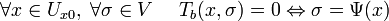
Or l'égalité Tb(x, σ) = 0 signifie que σ est une solution locale de l'équation différentielle avec la condition de Lipschitz σ(0) = x. Dit autrement :
![\forall t \in ]-b,b[,\;\forall x \in U_{x0} \quad \Psi(x)(t) = \beta(t,x)](https://static.techno-science.net/illustration/Definitions/autres/8/8c53cd2d08c713c9246dd491e2c32ae1_d87e73d5692539232f58e089b38d2750.png)
Soit x un élément de Ux0 et h un élément de E tel que x + h soit aussi élément de Ux0. La définition du fait que Ψ soit différentiable se traduit par :

Ce qui s'écrit encore :
![\forall \epsilon > 0,\; \forall t \in ]-b,b[,\;\exists \mu >0 \quad \|\beta(t,x+h) - \beta(t,x) - D\Psi_x(h)(t)\| \le \epsilon\|h\|](https://upload.wikimedia.org/math/5/a/1/5a174fcafc9e9a5b55a5326d05d27124.png)
La dernière majoration montre que le flot local β admet bien une différentielle partielle par rapport à sa seconde variable et qu'elle est égale au point (t, x) à h → DΨx(h)(t). Cette différentielle partielle est continue, les deux différentielles partielles de la coulée sont continues (la première est égale à la dérivée d'une courbe intégrale), la fonction β est bien de classe C1.
-
- Si f est de classe Cp le flot local β l'est aussi :
Le flot β vérifie l'égalité :
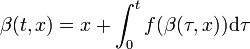
La première dérivée partielle de β vérifie l'égalité :
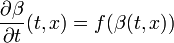
Elle est composée de fonctions de classe C1 et est donc de classe C1.
Le fait que f et β soit tous deux de classe C1 autorise une dérivation sous le signe somme, et :
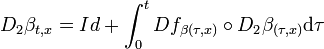
En différentiant par rapport à la première variable t, on obtient :
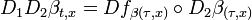
On en déduit que D2βt, x est solution d'une équation différentielle non autonome de type (2), définie par un champ de vecteurs temporel de classe C1. On en déduit que D2βt, x est une application de classe C1. les deux différentielles partielles de Dβ sont de classe C1, ce qui montre que β est de classe C2. En poursuivant par récurrence, on achève la démonstration de la proposition.
Régularité du flot global
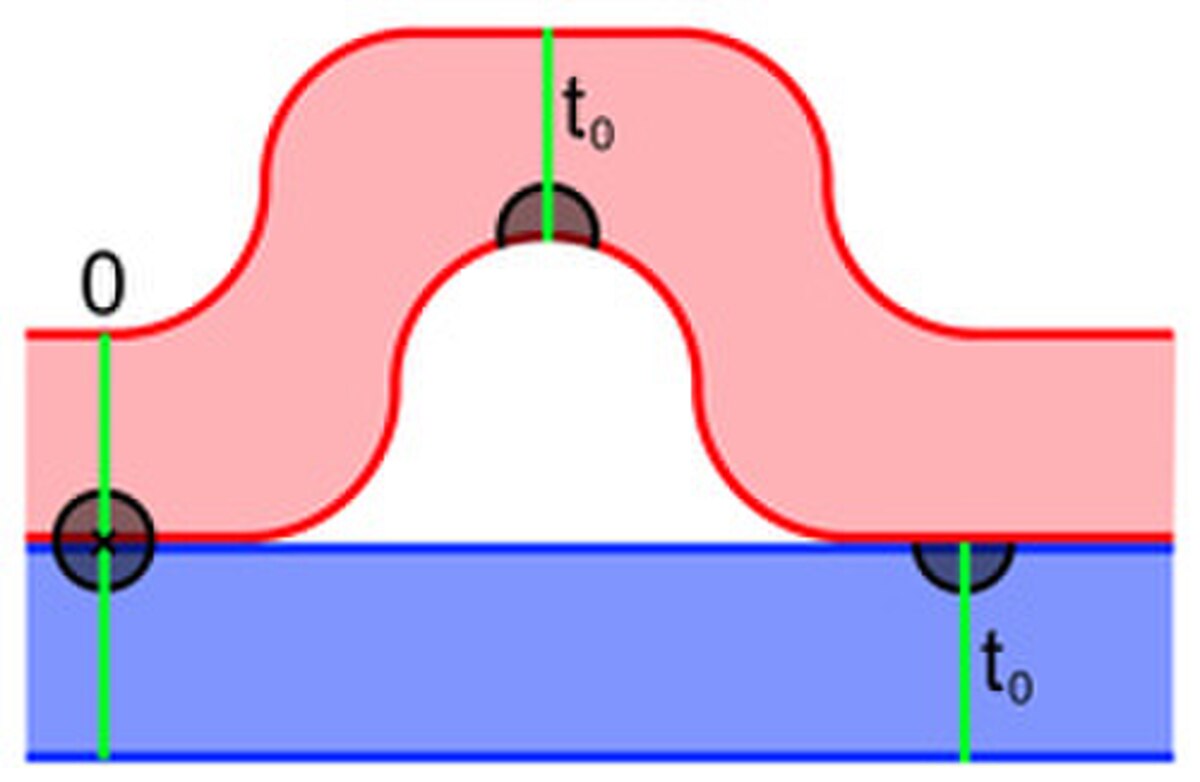
Pour généraliser les propriétés au flot global, il reste encore un peu de travail. Il s'agit surtout de montrer que la configuration de droite ne peut pas se produire. En reprenant la métaphore de l'introduction, on suppose que l'étang contient un rocher. Sur la zone rouge, le flot contourne le rocher, sur la zone bleu il passe tout droit. Le flot possède alors des points de discontinuité. Pour s'en rendre compte, on considère l'évolution d'un voisinage d'un point symbolisé par une zone grise circulaire à un instant 0, sur la figure de droite. Ce point est situé à la frontière des deux zones. À l'instant t0, ce voisinage est découpé en deux parties éloignées l'une de l'autre. Cette configuration peut se produire, par exemple si Ω n'est pas un ouvert. En revanche, dans les hypothèses étudiées, cette configuration est impossible.
Certaines propriétés sont plus simples à démontrer que la continuité. Le théorème de Cauchy-Lipschitz, sous sa forme élémentaire garantit à la fois l'existence et l'unicité du flot global α et de son domaine de définition. Il assure aussi que le flot global est dérivable par rapport à la première variable et que la dérivée partielle, considérée comme une fonction de t, est continue. Le paragraphe précédent apporte aussi des informations. Il établit que si t est proche de 0 et si t et x varient peu, le flot est de classe Cp, si f l'est. En revanche, la continuité du flot global α suppose aussi que l'expression α(t, x) soit continue en x, même si t n'est pas proche de 0. On a supposé ici que (t, x) est un point du domaine de définition de α.
Une remarque est utile, valable uniquement pour les équation autonomes. Le point β(s, x) désigne la position, à l'instant s, du point qui était en x à l'instant 0. Le point β(t, β(s, x)) désigne la position à l'instant t, du point qui était en β(s, x), à l'instant 0. Il désigne aussi la position à l'instant s + t du point qui était en position x à l'instant s. Ce qui signifie, si les différentes valeurs sont dans les bons domaines de définitions :
Ainsi, si les domaines de définitions s'y prêtent, il est possible de combiner les flots locaux, pour en construire un plus vaste. Cette technique permet de munir les flots locaux d'une structure de semi-groupe. Si le flot global est toujours défini sur R, les solutions intégrales maximales partageant une portion de domaine de définition, forment une structure de groupe, image de R par un morphisme de groupes. Cette remarque et utilisée afin de montrer le résultat suivant :
-
- Lemme 1 : Le flot global d'une équation différentielle autonome existe et est unique, il est défini sur un ouvert, continue, dérivable par rapport à la première variable et localement lipschitzien par rapport à la deuxième.
Une fois ce résultat établi, il est simple de le généraliser :
-
- Théorème : Le flot global d'une équation différentielle à paramètre existe et est unique. Il est défini sur un ouvert. Si le champ de vecteurs f est de classe Cp le flot global l'est aussi.
-
- Le flot global d'une équation différentielle autonome est de classe C et défini sur un ouvert :
On suppose évidemment que f est de classe Cp. Soit (t, x) un point du domaine de définition de α, avec t positif. L'objectif est de montrer l'existence d'un ouvert contenant (t, x), inclus dans le domaine de définition du flot et tel que α soit de classe Cp sur cet ouvert. Un raisonnement analogue montre que si t est négatif, un ouvert de même nature existe, ce qui permet de conclure.
Par définition, x est une image par une courbe intégrale maximale, soit tM la borne supérieure de son intervalle de définition (qui peut être infinie) et x0 l'image par cette courbe intégrale de la valeur 0. On définit une propriété P pour les réels de l'intervalle [0, tM[, la propriété P est vérifiée pour la valeur t, s'il existe un voisinage Vt de x0 et un intervalle ouvert It contenant [0, t] tel que le produit ItxVt soit contenu dans le domaine de définition du flot et que α soit de classe Cp sur ce produit. L'analyse locale montre que 0 vérifie cette propriété. Soit tP, la borne supérieure des réels de l'intervalle [0, tM[, vérifiant la propriété P. La démonstration consiste à prouver que tP est égal à tM. Si tel est le cas, comme t est strictement plus petit que tM (le domaine de définition d'une courbe intégrale maximale est un ouvert) il est strictement plus petit que tP et le point (t, x) est élément d'un ouvert ItxVt inclus dans le domaine de définition du flot, et tel que α soit de classe Cp sur cet ouvert. L'application β est, d'après un résultat précédent, de classe Cp.
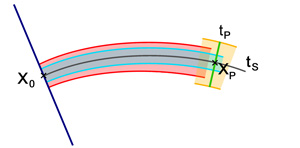
Supposons que tP soit strictement plus petit que tM. Sur la figure de droite, la ligne grise contenant x0 et xP (défini comme étant égal à α(tP, x0)) est la courbe intégrale de condition de Cauchy (0, x0). Le résultat précédent montre l'existence d'un flot local β définie au voisinage de (0, xP). Ce voisinage contient un produit cartésien JxW, où J est l'intervalle ouvert ]-b, b[ défini dans le paragraphe sur le flot local et W un ouvert contenant xP, par exemple la boule fermée de centre xP et de rayon a. L'image cet ouvert par β est illustrée en orange sur la figure de droite.
L'objectif est maintenant de raccorder ce flot local avec un voisinage de (0, x0). Soit μ, un réel strictement positif, strictement plus petit que b et que tP, tel que β(-μ, xP) soit dans W. Un tel μ existe car le flot local β est continu. Par définition de tP, le couple (tP - μ, x0) est dans le domaine de définition où α est de classe Cp (en rouge sur la figure). Soit V l'image réciproque de W par l'application, qui à x associe α(tP - μ, x), restreint au domaine de définition où elle est de classe Cp. V est un ouvert car image réciproque d'un ouvert par une application continue. Cet ouvert contient x0, car μ a été choisi de telle manière à ce que α(tP - μ, x0) = β(-μ, xP) soit dans W. L'unicité du flot sur JxW montre que :
![\forall t \in ]t_P - b-\mu,t_P-\mu[ ,\;\forall x \in W \quad \alpha(t,x) = \beta (t-t_P+\mu,\alpha(t_P-\mu,x))\;](https://static.techno-science.net/illustration/Definitions/autres/a/ab9c107765e5a917bed11f20bba0a0eb_335862ed9dff698fb3a484f63214e446.png)
Comme β est de classe Cp, il est possible de prolonger α sur l'ouvert [0, tP + b - μ[xW (en gris bleu sur la figure) de telle manière à ce que la restriction de α à ce nouveau domaine soit toujours de classe Cp. La valeur tP ne peut pas être la borne supérieure des réels vérifiant la propriété P, car la valeur tP + b - μ vérifie cette propriété. Cette contradiction montre que tP est égal à tM et que le point (t, x) est inclus dans un ouvert support d'un flot local de classe Cp. On en déduit que tout point du domaine de définition de α est contenu dans un ouvert α soit défini et de classe Cp sur cet ouvert, ce qui termine la démonstration.
-
- Si l'équation est non nécessairement autonome et à paramètre, le flot global est de classe Cp, si f l'est :
Un paragraphe précédent montre qu'une équation différentielle à paramètre se ramène toujours à une équation différentielle autonome. Le résultat précédent permet de conclure.

















































