Fonction d'état - Définition

Introduction

Une fonction d'état est une fonction des variables d'état qui décrivent les états d'équilibre d'un système thermodynamique. Physiquement, une telle fonction possède la propriété de ne dépendre que de l'état d'équilibre dans lequel se trouve le système, quel que soit le chemin emprunté par le système pour arriver à cet état. Au cours d'une transformation entre deux états d'équilibre, la variation d'une fonction d'état ne dépend donc pas du chemin suivi par le système pendant la transformation mais dépend uniquement des états d'équilibre initial et final. Ceci permet de déterminer cette variation pour n'importe quelle transformation, y compris une transformation irréversible, en définissant un chemin réversible pour lequel le calcul est possible.

Les potentiels thermodynamiques sont des fonctions d'état particulièrement importantes. Dans le cas le plus général en revanche, le travail et la chaleur échangés pendant une transformation ne peuvent pas être écrits sous la forme d'une variation d'une fonction d'état ; ils dépendent de la nature de la transformation. Néanmoins il existe des cas particuliers où la chaleur et le travail ne dépendent plus du chemin suivi lorsque les transformations s’effectuent soit à pression constante (voir enthalpie), soit à volume constant (voir énergie interne).

Mathématiquement, la possibilité de représenter une grandeur physique par une fonction d'état est liée aux propriétés de sa forme différentielle, c'est-à-dire sa variation dans une transformation infinitésimale autour d'un état d'équilibre.

Exemple de compréhension

Considérons la fonction altitude A lors d’une randonnée en montagne. L'« état » du groupe de randonneurs peut être défini par exemple, par ses coordonnées GPS permettant de le situer sur le chemin de randonnée. Supposons que pour aller d’un sommet (1) à 2500 m à un sommet (2) à 2600 m, deux chemins s’offrent au groupe :

• un premier chemin qui suit la ligne de crête presque au niveau des deux sommets,

• un deuxième chemin qui redescend dans la vallée à 500 m d’altitude.

La variation d’altitude ΔA est la même pour les deux chemins :

• ∆A = A(2) – A(1) = 100 m

La fonction altitude pourrait être considérée comme une fonction d’état de la randonnée. En revanche, les efforts consentis, travail et chaleur dégagée par les randonneurs ne seront pas identiques ! Ces grandeurs ne seraient donc pas des fonctions d’état mais des grandeurs liées au chemin suivi.

Équation d’état

Les variables d’état définissant l’état d’équilibre d’un système, p, V, T, n, ne sont pas indépendantes. Elles sont liées par une relation appelée équation d’état du système, plus ou moins complexe.

Par exemple, l’équation d’état la plus simple est celle du gaz parfait. C'est le modèle idéalisé d'un gaz constitué de particules suffisamment éloignées les unes des autres pour considérer qu'il n'y a aucune interaction d'ordre électrostatique entre elles ; cela implique que la pression est faible. Dans ces conditions, l'équation d'état est indépendante de la nature chimique du gaz considéré comme parfait. De nombreux gaz réels dans les conditions normales de température et de pression vérifient, avec une excellente approximation, le modèle du gaz parfait; c'est le cas des gaz constituants de l'air : le diazote (N₂) et le dioxygène (O₂).

Elle s'exprime par la relation:

• , où R est la constante des gaz parfaits, R = 8,314 J.K^-1.mol^-1)

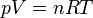
En mesurant T et p pour n (mol.) de gaz parfait on peut alors calculer le volume et définir parfaitement son état d'équilibre :

Pour définir l’état d’une quantité donnée d'un gaz parfait (n fixé), 2 variables indépendantes suffisent (cette propriété peut être étendue à tous les corps purs, qu'ils soient solides, liquides ou gazeux).