Forme trace - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Si l'extension L est galoisienne l'égalité suivante est vérifiée :
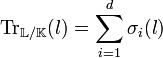
Ici la famille (σ1, σ2, ..., σd) décrit les éléments du groupe de Galois. La trace est égale au coefficient du monôme sous-dominant du polynôme caractéristique χ[X]. Ce polynôme s'exprime comme un multiple du polynôme minimal P[X] de la manière suivante :
![\chi[X] =\prod_{i=1}^d \Big(\sigma_i(m) - X\Big)=(-1)^n P^n[X]](https://static.techno-science.net/illustration/Definitions/autres/7/7fa50e9bb2fe185ecdeb58f8e7c851c0_32fcb030b530dbe14f752d8edf8a182b.png)
La démonstration est donnée dans l'article Polynôme minimal d'un nombre algébrique
Par définition, la forme trace prend ses valeurs dans K.
On remarque que la forme trace est symétrique. Elle bénéficie de plus de la propriété suivante :
-
- La forme trace est non dégénérée si et seulement si l'extension L est séparable.
-
- Supposons que l'extension L soit séparable :
Pour montrer que la forme trace est non dégénérée, il suffit d'expliciter une expression matricielle de cette forme et de calculer son déterminant. S'il est non nul, alors la forme trace est non dégénérée. Il suffit de trouver une base qui offre une expression simple de cette matrice.
Si l'extension est séparable, il existe un élément p primitif (cf théorème de l'élément primitif), c'est-à-dire que la famille (1, p, ..., pd) forme une base de L. Soit M = (mij) la matrice de la forme trace dans cette base. Alors :
![\forall i,j \in [1,d]\quad m_{ij} = \text{Tr}(\varphi_{p^{i+j}})](https://static.techno-science.net/illustration/Definitions/autres/2/2407f2a38c44c187e3abe7170357eb9f_90afce20ae18ce4a97ce631023747166.png)
Soit P[X] le polynôme minimal de p. Il est de degré d la dimension de L et son polynôme minimal est égal à son polynôme caractéristique (à un facteur (-1)d près). Dire que L est séparable revient à dire que P[X] n'admet aucune racine multiple. Soit D le corps de décomposition de P[X] et λk pour k variant de 1 à d les racines toutes distinctes de φp. Considérons l'espace vectoriel E obtenu par le produit tensoriel de D et du K espace vectoriel L. L'espace E est simplement l'espace vectoriel L de dimension d prolongé sur le corps des scalaires D. La forme trace se prolonge sur E et son expression matricielle est la même que celle de l'espace L. En revanche, l'endomorphisme de matrice M est maintenant diagonalisable car le polynôme minimal est scindé et séparable. Comme le changement de base ne modifie pas le déterminant, il est possible de calculer ce déterminant dans E et dans la base de vecteurs propres.
Les valeurs propres de φpi+j comme endomorphisme de E sont en conséquence, égales à λ ki+j. Ce qui donne une expression de la trace, en remarquant qu'elle est égale à la somme des valeurs propres :
![\forall i,j \in [1,d]\quad m_{ij} = \text{Tr}(\varphi_{p^{i+j}}) = \sum_{k=1}^d \lambda_k^{i+j}= \sum_{k=1}^d \lambda_k^i.\lambda_k^j\quad \text{et}\quad M = {}^tA\cdot A](https://static.techno-science.net/illustration/Definitions/autres/e/e70a88d46d1ccf6a27568e7668a91a21_4e468595eb827e49f20149ebc26fae53.png)
Si A désigne la matrice égale à (λ ki ). Il suffit donc de démontrer que le déterminant de la matrice A est non nul pour conclure. Or A est une matrice de Vandermonde à coefficients tous distincts et son déterminant n'est pas nul (l'article associé montre qu'une matrice de Vandermonde est inversible si les valeurs λk sont distincts).
-
- Supposons que l'extension L soit non séparable :
La démonstration est donnée dans le livre Algèbre de Serge Lang.

















































