Fraction continue d'un nombre quadratique - Définition
La liste des auteurs de cet article est disponible ici.
Période
Une autre propriété simplifie la détermination d'un nombre quadratique sous forme de fraction continue :
-
- Un irrationnel x possède un développement en fraction continue périodique à partir d'un certain rang si et seulement si x est solution d'une équation du second degré à coefficients rationnels.
Si le développement de x est périodique à partir du rang p alors il existe un entier n tel que l'égalité suivante soit vérifiée. Ce qui justifie la notation, déjà utilisée dans le préambule :
![x =[a_0, a_1,\cdots, a_{p-1}, a_p,\cdots a_n,a_p, a_{p+1}\cdots \;] =[a_0, a_1,\cdots, a_{p-1},\overline{a_p, a_{p+1},\cdots a_n}]\;](https://static.techno-science.net/illustration/Definitions/autres/4/46f4084079184bb8eb8f83db0cec1b24_e056673cd73a6a6605aa5e671ab3ba44.png)
Cette proposition est au cœur de l'intérêt de la notion de fraction continue pour les nombres quadratiques. Autant il est relativement simple de montrer qu'un nombre ayant une fraction continue périodique à partir d'un certain rang est nécessairement quadratique, autant la réciproque est un peu plus délicate. Sa preuve date de plus d'un siècle après la découverte de cette propriété et est l'œuvre de Lagrange. La démonstration présentée ici est relativement proche de l'originale.
-
- Soit x un nombre réel, s'il admet un développement en fraction continue périodique à partir d'un certain rang, il possède un polynôme minimal de degré deux. :
Le polynôme minimal d'un nombre algébrique est le polynôme de plus petit degré et de monôme dominant ayant pour coefficient 1, qui admet pour racine cet entier. Par hypothèse, le développement de x est périodique à partir d'un certain rang, noté p. On en déduit, si xp désigne le quotient complet d'indice p de x, l'égalité suivante :
![x_p = [a_p, a_{p+1},\cdots, a_n, x_p]\;](https://static.techno-science.net/illustration/Definitions/autres/e/ee83c4da328776cd749544cc1de526a6_543ffae2cf6ff4058459abe4dbc4b0b7.png)
Si hn' (resp. kn' ) désigne le numérateur (resp. le dénominateur) de la fraction continue [ap, ap+1, ..., an], l'égalité suivante, conséquence d'une propriété démontrée dans l'article Fraction continue, est vérifiée :
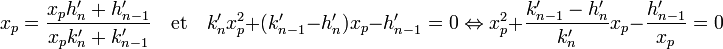
Et xp possède un polynôme minimal de degré au plus deux. La valeur x est somme d'un rationnel : la réduite d'indice p et d'un irrationnel quadratique, la caractérisation des nombres quadratiques du paragraphe précédent montre que cette contidion est suffisante pour que x soit quadratique.
-
- Soit x un nombre nombre quadratique, il admet un développement en fraction continue périodique à partir d'un certain rang :
Le principe de la méthode utilisée consiste à associer une forme quadratique à chaque quotient complet, provenant de son polynôme minimal. L'analyse de ces formes quadratiques montre qu'il ne peut en exister qu'un nombre fini, le quotient complet apparaît comme une racine du polynôme associé. Il n'existe que deux racines pour chaque polynôme, soit au total qu'un nombre fini possible de quotients complets. La suite des quotients complets se répète, d'où son caractère périodique.
Par hypothèse, x est racine d'un polynôme du second degré à coefficients rationnels, noté ici α.X2 + β.X + γ. On associe à ce polynôme la forme quadratique φ :
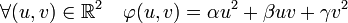
Dans le même ordre d'idée, on associe au quotient complet d'indice j la forme quadratique φj définie par :
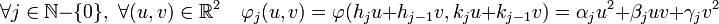
Un développement de l'expression définissant φj en fonction des coefficients de φ et des suites (kj) et (hj) montre l'existence des trois coefficients αj, βj et γj définis par l'égalité précédente.
La définition du quotient complet montre l'égalité :
![\forall j \in \mathbb N - \{0\}\quad x = [a_0,a_1,\cdots,a_j,x_j]\quad\text{et}\quad x = \frac {h_jx_j + h_{j-1}}{k_jx_j + k_{j-1}}\;](https://static.techno-science.net/illustration/Definitions/autres/7/72de31bee970484f381e3d2a1f13e3d4_b80d3aa61ebbe039a60e0cfad16920d8.png)
On en déduit que :
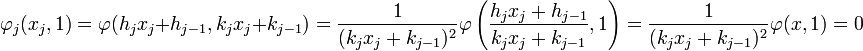
-
- La suite des coefficients (αj) est bornée en valeur absolue :
La définition de φj et le fait que φ(x, 1) soit nul montrent que :
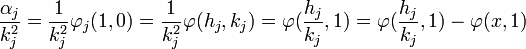
On en déduit :
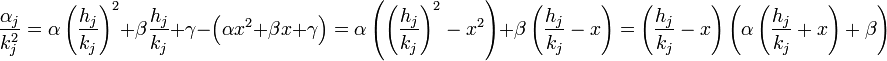
La fraction hj / h k est une approximation dont la distance à x est toujours inférieure à 1/kj2. On en déduit que hj / h k + x est en valeur absolue inférieur à 2|x| + 1 et :
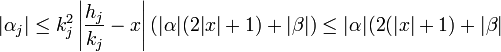
Ce qui démontre l'assertion.
-
- La suite des coefficients (γj) est bornée en valeur absolue :
Il suffit de remarquer que γj est égal à αj-1 car :
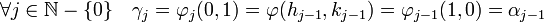
Le caractère majoré de la suite (αj) permet de conclure.
-
- La suite des coefficients (βj) est bornée en valeur absolue :
Ici réside l'essentiel de l'astuce de la démonstration de Lagrange. Il remarque que le discriminant dj du polynôme φj(X,1) possède aussi une lecture par un déterminant. Cette propriété permet de montrer que tous les discriminants des polynômes φj(X,1) sont égaux à celui du polynôme φ(X,1) noté ici d. Par voie de conséquence, la suite (βj) est aussi bornée.
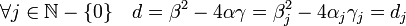
Pour s'en convaincre, notons B la base canonique de R 2 et ψj l'endomorphisme de R 2 de matrice Mj dans la base canonique B, donnée par l'égalité suivante, un calcul de déterminant montre (le dernier calcul provient d'un résultat démontré dans l'article Fraction continue) :

La matrice Φ de la forme quadratique φ ainsi que celle de ψj donnent une expression matricielle Φj de la forme quadratique φj. Il suffit alors de remarquer que d (resp. dj) est égal à -4 fois le déterminant de la matrice Φ (resp. Φj) pour conclure :
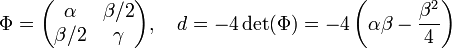
On en déduit :
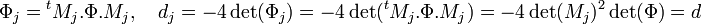
-
- Conclusion:
Les trois suites (αj), (bj) et (cj) sont bornées en valeur absolue, il ne peut exister qu'un nombre fini de polynômes différents de la forme αj.X2 + βj.X + γj. Un quotient complet est une racine d'un des polynômes précédemment cités, il ne peut en exister qu'un nombre fini. Il existe deux entiers n et p tel que xp-1 soit égal à xn. On en déduit que a p est égal à an+1 et xp à xn+1 et donc que ap+1 et égal à an+2 et ainsi de suite. Ceci montre le caractère périodique de la suite (a j).