Fraction continue d'un nombre quadratique - Définition

Un exemple historique de résolution de l'équation de Pell Fermat

L'équation suivante possède une longue histoire :

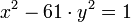
Brahmagupta l'utilise comme illustration d'un ancêtre de la méthode chakravala dès le VI^e siècle. À cette époque, les nombres négatifs n'étaient pas considérés. Il est repris par Bhāskara II qui perfectionne la méthode et lui donne une puissance algorithmique un peu supérieure à celle par les fractions continues, présenté ici.

Le 3 janvier 1658, l'exemple est encore repris par Pierre de Fermat, qui en fait un défi lancé aux mathématiciens de toute l'Europe. Fermat conclut par « si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise ». Ce défi est à l'origine des travaux anglais sur les fractions continues des nombres quadratiques et leur connexion avec l'équation de Pell Fermat.

Appliquons l'algorithme des fractions continues pour calculer les coefficients et les quotients complets :

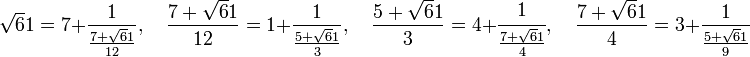
Ce qui donne les premiers coefficients : 7, 1, 4, 3. On continue avec :

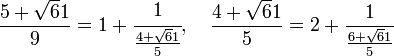
On dispose maintenant de la section commençante 7, 1, 4, 3, 1, 2. Il n'est plus nécessaire de continuer. On remarque que les quotients complets x₅ et x₆ sont associés ce qui se remarque au fait qu'ils ont le même dénominateur. La moitié du palindrome est déjà explicitée. Comme ce phénomène se produit pour deux indices adjacents, on peut en déduire que la période est impaire et égale à 2 x 5 + 1. On peut aussi en déduire que a₆ est égal à a₅, ainsi que les termes suivants : 2, 1, 3, 4, 1. Enfin, le dernier terme est égal au double du premier, soit 14. Le premier candidat à la solution est donc celui mise en valeur en rouge dans l'expression suivante :

On sait que la fraction réduite d'indice 10, appliquée à l'équation du paragraphe donne 1 en valeur absolue. Pour la calculer, le plus simple est de commencer par utiliser les relations de récurrences (cf l'article Fraction continue). Si h_n / k_n désigne la réduite d'indice n et a_n le coefficient d'indice n, on dispose des formules :

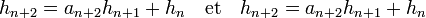
En remarquant que la première et la deuxième réduite sont égales à 7/1 et 8/1, on obtient :

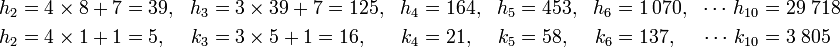
Cependant, comme l'indice de la réduite calculée est pair, la solution associée à l'équation du paragraphe est de signe est négatif, ce qui se vérifie aisément :

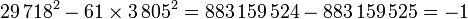
Ni Brahmagupta, ni Fermat n'acceptent ce type de solution. La bonne réduite est donc la 21^ième. Pour la calculer, on peut soit prolonger le calcul, soit utiliser le même principe que celui de la deuxième méthode d'extraction d'une racine :

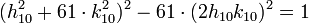
L'article équation de Pell-Fermat montre que cette formule donne exactement la solution associée à la 21^ième réduite de la fraction continue. La solution du défi de Fermat est :

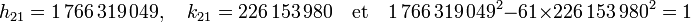
Extraction d'une racine carrée

Première méthode

Les propriétés de la fraction continue d'un nombre quadratique permettent de calculer des approximations des racines carrées. La première technique consiste simplement à calculer les coefficients de la fraction continue puis ses réduites. Si l'on cherche la racine de 3, on trouve dans un premier temps :

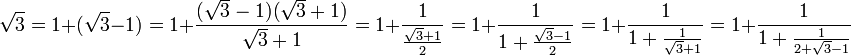
Le quotient complet (√3 - 1)^-1 égal à 1/2.(√3 + 1) a déjà été développé en fraction continue, on en déduit l'expression :

Les réduites se calculent par des formules de récurrences, étudiées dans l'article Fraction continue. Si h_n / k_n sont ces réduites :

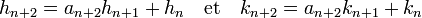
Ce qui donne les approximations suivantes de la racine de trois :

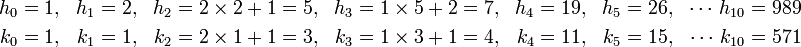
Ainsi, à la 10^ième étape, on obtient la fraction 989 / 571, approximativement égale à 1,732 049 alors que les 7 premiers chiffres significatifs exacts sont 1,732 051. La précision de cet algorithme à l'étape n est meilleure que 1/(2k_n²) d'après les calculs précédents. Pour l'approximation d'indice 10, on sait donc que l'erreur est inférieure à 1/(2x571²) meilleure que le 600 000^ième. Une force de cet algorithme est la qualité des solutions proposées, au sens où toute fraction de type a/b avec b strictement inférieur à 571 sera nécessairement moins bonne que la dixième réduite de la fraction continue. Par exemple, la meilleure approximation décimale de la racine de trois avec deux chiffres significatif, égale à 17/10, commet une erreur supérieur au 50^ième. Celle un peu équivalente 19/11 correspondant à la réduite d'indice 4 propose une approximation au 200^ième, soit quatre fois meilleure. Cette propriété est démontrée dans l'article Fraction continue et approximation diophantienne.

Accélération violente

L'étude de l'équation de Pell-Fermat permet d'imaginer un algorithme dont la convergence est beaucoup plus rapide. Étudions le cas général. La réduite d'indice n est solution de l'équation de Pell-Fermat suivante si n + 1 est la période de la fraction continue associée à la racine de d, un entier non carré parfait :

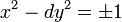
L'égalité suivante montre, qu'à partir une solution (h_n, k_n), il est possible d'en construire une nouvelle, en considérant le carré de l'équation :

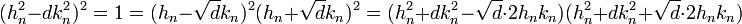
En appliquant à nouveau l'identité remarquable traitant de (a - b)(a + b), on obtient :

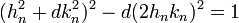
Si l'on note u_j et v_j le numérateur et le dénominateur de cette suite, elle est définie par récurrence :

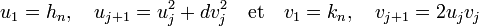
L'application au cas de la racine de 3 donne pour première valeur 2/1, en effet, 2² - 3 x 1² = 1 est bien la première solution non triviale, on trouve ensuite :

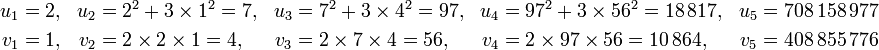
Il n'existe peu d'applications nécessitant d'aller au-delà de l'étape 5, la précision de u₅ / v₅ dépasse déjà 20 décimales. Tous ces couples de numérateurs et dénominateurs sont des solutions de l'équation de Pell-Fermat, la théorie indique que ce sont des réduites de la fraction continue de la valeur recherchée, ici la racine de trois. En conséquence, la précision est toujours meilleure que l'inverse du double du carré du dénominateur.