Fraction continue d'un nombre quadratique - Définition

Introduction

Joseph-Louis Lagrange établit de manière rigoureuse les propriétés des fractions continues des nombres quadratiques.

En mathématiques et plus précisément en arithmétique la fraction continue d'un nombre quadratique correspond à la représentation de ce nombre sous la forme suivante :

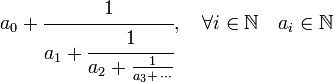
Si le nombre représenté est quadratique, c'est-à-dire s'il n'est pas rationnel mais solution d'une équation du second degré à coefficients rationnels, alors la suite d'entiers (a_n) est périodique à partir d'un certain rang.

L'intérêt de l'étude de la fraction continue d'un nombre quadratique ne se résume pas à cette anecdote. La simplicité de l'algorithme permettant de déterminer les coefficients de la fraction en ont fait pendant longtemps une méthode d'extraction de racine. La connaissance de la fraction continue permet aussi de résoudre une célèbre équation diophantienne, c'est-à-dire une équation dont les coefficients et les solutions recherchées sont des nombres entiers. Cette équation porte le nom de Pell-Fermat et prend la forme suivante, si n est un entier sans facteur carré.

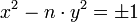
Préambule

Introduction par l'exemple

Le calcul de la fraction continue d'un nombre quadratique est relativement aisée, l'identité remarquable (a + b)(a - b) = a² - b² est utilisée à chaque étape. L'exemple suivant en est une illustration :

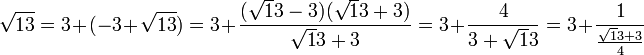
et

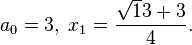
Il est possible d'appliquer à nouveau le même algorithme sur x₁ :

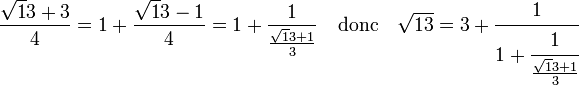
et

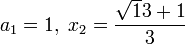
Puis sur x₂ :

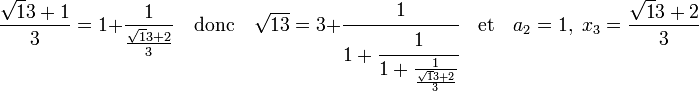
Avec, ensuite :

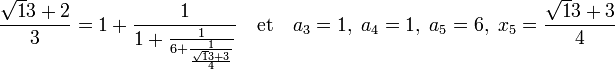
Le vocabulaire et les notations utilisés ici sont ceux définis dans l'article Fraction continue. Le coefficient d'indice n de la fraction continue correspond au coefficient a_n utilisé dans l'introduction. La réduite d'indice n désigne la fraction continue tronquée contenant n barres de fraction et construite à l'aide de n + 1 coefficients, elle est notée h_n / kn. Le quotient complet est la valeur, noté x_n tel que si l'on remplace a_n-1 par a_n-1 + 1/ x_n dans l'expression de la réduite d'indice n - 1, on obtient exactement le nombre initial. Le quotient complet x₀ est la valeur initiale, √13 dans l'exemple choisi.

Le coefficient a_n correspond à la partie entière du quotient complet x_n et le quotient complet x_n+1 à l'inverse de la partie fractionnaire de x_n. Pour résumer, on obtient :

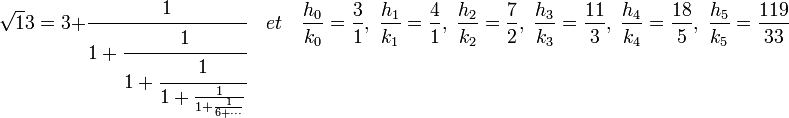
Cette notation étant un peu lourde, on utilise de préférence la suivante, ayant la même signification :

Enfin, que le quotient incomplet x₅ est égal à x₁, ce qui permet de conclure que la suite des coefficients se répète à partir du rang 1. On parle de suite périodique à partir d'un certain rang et on utilise la notation :

La barre utilisée ici est d'un usage fréquent dans la littérature. Elle signifie une répétition à l'infini de la suite d'entiers couverte par la barre.

Eléments d'histoire

Dès le VI^e siècle, Âryabhata , un mathématicien indien, utilise les fractions continues pour obtenir des rationnels proches de racines carrés. Si Brahmagupta un autre mathématicien indien s'intéresse à l'équation de Pell-Fermat et améliore la méthode dite chakravala pour la résoudre, il faut attendre le XII^e siècle et Bhāskara II pour voir une approche analogue à celles des fractions continues appliquées à cette équation. Son algorithme correspond à celui de l'article à la différence que a₀ est défini comme la plus proche valeur entière du nombre à approcher et non celle toujours inférieure. Cette différence est reportée à tous les coefficients a_n qui peuvent devenir négatifs. Cette spécificité, accélère un peu la recherche de la solution.

Ce n'est que plus tard que l'Europe s'intéresse à une démarche de cette nature. Il faut attendre le XVI^e siècle pour que Rafael Bombelli fasse usage d'un ancêtre des fractions continues pour le calcul d'approximations de la racine carrée de 13. Pietro Antonio Cataldi comprend la portée de la méthode de Bombelli et l'applique à toutes les racines carrées, dans un petit opuscule à ce sujet, il choisit l'exemple de la valeur 18.

A la suite d'un défi lancé par Pierre de Fermat en 1657, William Brouncker , trouve de manière empirique les relations qui relient la fraction continue d'un nombre quadratique à l'équation de Pell-Fermat. Il est probable que Bernard Frénicle de Bessy connaissait aussi cette méthode pour résoudre l'équation de Pell-Fermat dont il trouve toutes les solutions pour n plus petit que 150, ces travaux ont été perdus. Il défie Brouncker de trouver une solution à l'équation pour n = 313. Dans sa réponse, il indique qu'il ne lui a pas fallu plus d'une heure ou deux pour la trouver. La réponse est la suivante, pas nécessairement immédiate à calculer manuellement :

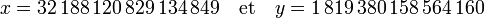
Ces informations proviennent d'une intense relation épistolaire entre les différents acteurs, qui est finalement publié par John Wallis

Le siècle suivant est celui des preuves. Leonhard Euler reprend les travaux de Brouncker et ceux de Wallis, et démontre rigoureusement tous les aspects un peu élémentaires de la théorie, il montre aussi si la représentation en fraction continue d'un nombre est périodique, à partir d'un certain rang, alors ce nombre est quadratique. Il faut encore attendre les travaux de Joseph-Louis Lagrange pour la démonstration d'une réciproque ainsi que des raisons de la validité de la méthode Bhāskara II ou de celle de Brouncker. Les propriétés de la fraction continue d'un nombre quadratique sont alors essentiellement élucidées, il ne reste plus qu'à comprendre dans quel cas une fraction continue n'est pas simplement périodique à partir d'un certain rang, mais périodique pure, ce qui est l'œuvre d'Evariste Galois .