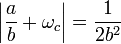Fraction continue d'un nombre quadratique - Définition

Première propriété

Le calcul pratique d'une fraction continue d'un nombre quadratique est simple. Une est raison est une conséquence de la propriété :

• Les quotients complets d'un nombre quadratique sont quadratiques.

Une manière de caractériser un nombre quadratique x est de trouver une racine √d d'un entier sans carré parfait et deux rationnels a et b tel que x soit égal à a + b.√d. Cette condition est nécessaire et suffisante. L'aspect nécessaire se déduit de la méthode de résolution d'une équation du second degré à l'aide du discriminant. Réciproquement, on peut remarquer que x est solution de l'équation, s'il est quadratique :

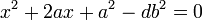
Si, dans sa décomposition en facteurs premiers d ne contient que des puissances paires, le nombre d est rationnel et x n'est pas quadratique mais rationnel, s'il en contient quelques uns, il est toujours possible de les extraire de la racine carrée et adjoindre ces facteurs au rationnel b.

La propriété énoncée se démontre par récurrence. À l'ordre 1, le quotient complet est la différence d'un entier et d'un nombre quadratique, il est donc quadratique. Supposons la propriété vraie à l'ordre n et montrons là à l'ordre suivant. x_n est un nombre quadratique, en conséquence a_n+1 - x_n est aussi un nombre quadratique. Notons le a + b.√d, la transformation suivante montre que (a + b.√d)^-1, égal au quotient complet d'indice n + 1 est aussi quadratique :

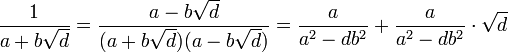
On remarque l'expression au dénominateur ne peut être nulle. Si elle l'était, la racine de d serait un rationnel et d ne pourrait être un entier sans facteur carré. Cette première propriété simplifie la recherche de l'expression d'un nombre quadratique sous forme de fraction continue, le calcul de l'inverse d'un nombre quadratique est simple. L'usage de l'identité remarquable : (a + b)(a - b) = a² - b² est en conséquence fréquente.

Equation de Pell-Fermat

Structure de la solution

La fraction continue est une technique à la fois théorique et pratique pour résoudre l'équation de Pell-Fermat suivante, si p est un entier sans facteur carré :

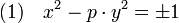
Une solution est un couple (a, b) d'entiers tel que a² - p.b² soit égal à plus ou moins un. Pour plus de simplicité dans les énoncées, ne sont considérées que les solutions dont les deux valeurs sont strictement positives. À part les solutions triviales (1, 0) et (-1, 0) toutes les autres se déduisent par multiplication ou non des deux termes a et b par -1. Trois propositions permettent de comprendre comment se structurent les solutions.

• Si (a, b) est un couple solution de l'équation (1), il existe un indice n tel que (h_n, k_n) soit égal au couple solution. Ici h_n et k_n désigne le numérateur et le dénominateur de la réduite de rang n de la valeur √p.

Autrement dit, toutes les solutions de l'équation se trouvent dans la suite des réduites de la fraction continue de √p.

Pour aller plus loin, il est nécessaire d'analyser la fraction continue de √p. Elle est de la forme, d'après le paragraphe précédent :

Notons k l'indice du coefficient a₁ qui se situe juste avant le coefficient 2a₀, c'est-à-dire celui en rouge dans l'expression précédente. Cela signifie que la période de la fraction continue est égale à k + 1.

• Un indice n correspond à une solution de l'équation (1) si, et seulement si, soit n est égal à k, soit il existe un entier positif q tel que n = k + q.(k + 1).

Ce qui signifie que les indices solutions sont ceux qui correspondent aux coefficients de valeur égale à a₁, qui se situe exactement avant le coefficient de valeur égale à 2.a₀. Il en existe exactement un par période.

• Si k est pair, il existe des solutions pour la valeur -1, elles correspondent aux indices k et k + 2q.(k + 1), les autres indices donne la valeur 1. Si k est impair, la valeur -1 n'est jamais atteinte.

Une autre manière d'énoncer cette proposition est de dire que la valeur -1 est atteinte si, et seulement si, la période est impaire, elle est alors atteinte une fois sur deux et la première solution est négative.

• Si (a, b) est un couple solution de l'équation (1), il existe un indice n tel que (h_n, k_n) soit égal au couple solution :

Cette proposition est une conséquence de la qualité de l'approximation par le rationnel h_n / k_n du nombre √p.

L'article Fraction continue et approximation diophantienne montre que si une fraction h / k approche un réel quelconque avec une précision meilleure que 1/2.k², la fraction est infailliblement une réduite de la fraction continue du réel. Si le couple est une solution de l'équation (1) :

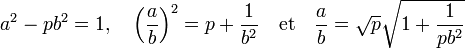
Or, la fonction qui à x associe 1 + 1/2.x majore la fonction √(1 + x) si x est positif. En remarquant que 1 est nécessairement plus petit que √p on en déduit :

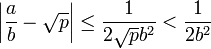
Ce qui impose à la fraction a / b d'être une réduite de √p et démontre la proposition.

• Un indice n correspond à une solution de l'équation (1) si, et seulement si, soit n est égal à k, soit il existe un entier positif q tel que n = k + q.(k + 1) :

Le paragraphe précédent contient les calculs permettant de prouver simplement cette proposition. Il suffit de montrer que h_n² - p.k_n² est égal, au signe près, au coefficient c_n défini au paragraphe précédent pour la détermination du palindrome. Une fois cette proposition démontrée, il ne reste plus qu'à déterminer dans quel cas c_j prend la valeur 1.

La valeur |h_n-1² - p.k_n-1²| est égale à c_n :

L'article Fraction continue montre que √p est égal à [a₀, a₁, ..., a_n-1,x_n] ce qui donne les égalités :

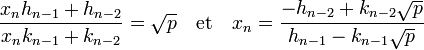
Ce que l'on peut encore écrire, avec les notations du paragraphe précédent :

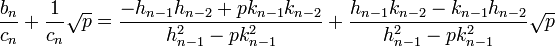
Comme (1, √p) forme une famille libre sur l'ensemble des rationnels, on en déduit, du fait que h_n-1.k_n-2 - k_n-1.h_n-2 est égal à (-1)ⁿ (cf l'article Fraction continue) :

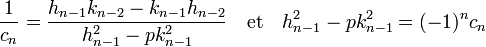
La valeur c_j est égale à 1 si, et seulement si, il existe un entier q tel que j = q.(k + 1) :

La suite des c_j est périodique de période k + 1, il suffit de montrer que dans l'intervalle des entiers j compris entre 1 et k + 1, uniquement le dernier vérifie c_j est égal à 1.

Montrons que c_k+1 est égal à 1. Par définition de k, x _k+2 est égal à a₀ + √p et a _k+2 = 2a₀. Le calcul suivant montre que b _k+2 est égal à a₀ et c _k+2 = p - a₀² :

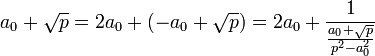
De plus, les calculs précédents ont établi que c_j.c_j+1 = p - b_j+1², donc :

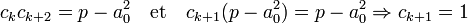
Réciproquement, montrons que si j est un entier compris entre 1 et k + 1 et si c_j est égal à 1, alors j est égal à k + 1. Si c_j est égal à 1, x_j est la somme d'un entier et de √p, sa partie fractionnaire égale à √p - a₀ et donc x_{j +1} à x _k+2, il correspond au dernier élément de la période, c'est-à-dire que j est égal à k + 1. L'indice de la réduire solution est précède k + 1, comme le montre le calcul de la proposition précédente, il est donc bien égal à k.

• Si k est pair, il existe des solutions pour la valeur -1, elles correspondent aux indices k et k + 2q.(k + 1), les autres indices donne la valeur 1. Si k est impair, la valeur -1 n'est jamais atteinte :

C'est une conséquence directe de l'égalité h_n-1² - p.k_n-1² = (-1)ⁿ.c_n. En remplaçant n par un multiple de k + 1, on obtient :

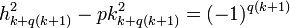
Si k est impair, seule la valeur 1 est obtenue, sinon une alternance de 1 et de -1 apparaît, la première valeur étant négative.

 

Groupe des unités

En théorie algébrique des nombres, il est parfois important de connaître la structure du groupe des unités d'un anneau d'entiers algébriques. Cette situation se produit en particulier pour les anneau d'entiers quadratiques. La compréhension de cette structure est utile, par exemple, de démontrer le dernier théorème de Fermat pour n = 3 ou 5, ou pour établir la loi d'apparition des nombres premiers dans la suite de Fibonacci (cf Entier du corps quadratique Q[√5]).

On est amené à trouver les éléments inversible de l'anneau Z[ω] qui sont de la forme a + b.ω ou ω est un entier quadratique et a et b des éléments de Z. On montre que cela revient à résoudre une des deux équations diophantienne suivante, ou d est un entier positif non carré parfait et f un entier positif tel que 4.f + 1 n'est pas un carré parfait :

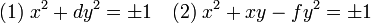
La première a déjà été étudiée, la deuxième est très similaire. On dispose par exemple de la propriété suivante :

• Si le couple (a, b) est solution de l'équation (2), alors a / b est une réduite de l'entier quadratique -ω_c défini par :

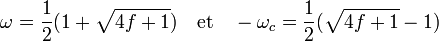
La notation un peu étrange de -ω_c pour indiquer l'entier quadratique approché provient du fait que ω est l'entier quadratique qui définit l'anneau Z[ω], ici le signe c en indice indique la valeur conjuguée. L'origine de ces formules est indiquée dans l'article entier quadratique.

Un calcul strictement analogue montre que l'avant dernier terme de la période de la fraction continue correspond aussi à la réduite recherchée.

Soit d l'entier égal à 4.f + 1. L'équation (2) s'écrit :

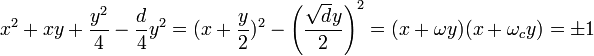
On remarque de ω = 1/2(1 + √d) et ω_c = 1/2(1 - √d). Soit (a, b) un couple solution de l'équation (2) tel que a et b soient positifs, On obtient :

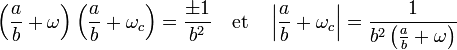
De par sa définition ω est strictement supérieur à 1. Si le couple (a, b) est solution de (2) alors a est supérieur à b et a / b aussi supérieur à 1. On obtient la majoration suivante, qui montre que a / b est une réduite de -ω_c :