Fraction continue d'un nombre quadratique - Définition

• Le développement de x est purement périodique si et seulement si x est strictement plus grand que 1 et x_c, le conjugué de x est compris entre -1 et 0 :

Cette démonstration procède en plusieurs étapes :

Si le développement en fraction continue de x est purement périodique, le quotient complet d'indice 0 : x₀ est quadratique, strictement plus grand que 1 et son conjugué x_c0 est donné par la formule suivante :

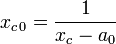
Les résultats précédents montrent que x est solution d'une équation du second degré. Soit P(X) le polynôme unitaire du second degré annulant x et considérons la fraction rationnelle composée de P(X) et de a₀ + 1/X. La multiplication de cette fraction rationnelle par X² est un polynôme Q(X) de degré 2 admettant x₀ pour racine, en effet :

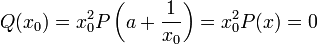
Le nombre x₀ est irrationnel, sinon x ne le serait pas. Il est de plus racine du polynôme Q(X) de degré 2 à coefficients rationnels, il est donc quadratique. Il est plus grand que 1 car tous les quotients complets le sont. Il l'est strictement car sinon x serait rationnel.

Il ne reste plus qu'à montrer la formule annoncée. L'application σ, qui à un élément de l'extension quadratique Q[x] associe son conjugué est un automorphisme de corps laissant Q invariant. Le conjugué d'un nombre quadratique de la forme a + b.√d, où a et b sont des nombres rationnels et d un entier sans facteur carré est le nombre a - b.√d. L'analogie avec la situation des nombres complexes est à l'origine de cette dénomination. L'égalité x₀(x - a₀) = 1, directement issue de la définition du quotient complet d'indice 0, montre que :

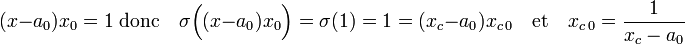
Si le développement en fraction continue de x est purement périodique, x est strictement plus grand que 1 et x_c est strictement compris entre -1 et 0 :

Soit a₀, a₁, ..., a_n la période de x, la partie entière de x est égale à a₀ et donc à a_n+1, ce qui montre que x est plus grand que 1, il est strictement plus grand, sinon il ne serait pas irrationnel.

On dispose de l'égalité x = [a₀, a₁, ..., a_n, x], ce qui montre (pour les détails voir l'article Fraction continue) :

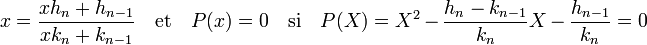
Le fait que x soit strictement positif montre que h_n-1 et k_n sont strictement positifs. La deuxième racine de P(X) est le conjugué x_c de x, le produit des racines x.x_c est égal à la constante du polynôme P(X) et est négative. Comme x est positif, x_c est strictement négatif.

Enfin, on remarque que P(-1) est strictement positif, en effet :

On remarque que P(-1) est strictement positif, P(0) strictement négatif, le théorème des valeurs intermédiaires montre que la racine négative x_c se situe strictement entre -1 et 0.

Si x est strictement plus grand que 1 et x_c est strictement compris entre -1 et 0, le développement en fraction continue de x est purement périodique :

La méthode consiste à montrer l'existence d'un entier n tel que, pour tout j strictement positif, a_j-1 est égal à a_j+n-1. Ainsi, a₀ est égal à a_n, a₁ est égal à a_n+1 etc... Pour ce faire, on procède en deux étapes :

La suite des quotients complets (x_j) est strictement supérieure à 1 et la suite (x_cj) des conjugués des quotients complets est strictement compris entre -1 et 0 :

Montrons ce résultat par récurrence sur j. Si j est égal à 0, la proposition est vérifiée par hypothèse. Supposons la propriété vraie à l'ordre j et montrons là à l'ordre j + 1. L'irrationnel quadratique x_j vérifie les hypothèses de la première proposition de cette boite déroulante. Son quotient incomplet d'indice 0 est égal à a_j et son quotient complet à x_j+1 et :

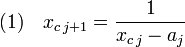
Par construction, a_j+1 est strictement positif, x_j est un irrationnel et est donc différent de 1, comme sa partie entière est au moins égal à 1, x_j est strictement plus grand que 1. De plus, x_cj est non nul et strictement négatif, ce qui montre que x_cj - a_j est strictement inférieur à -1, donc que x_j+1 est strictement compris entre -1 et 0.

Conclusion :

Le fait que x soit un irrationnel quadratique montre qu'à partir d'un rang p, la suite est périodique. Soit n cette période, c'est-à-dire :

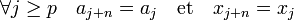
L'objectif est de montrer que p est égal à 0. Pour cela, considérons un entier m strictement positif et supérieur ou égal à p, montrons que m est strictement plus grand que p. L'égalité (1) montre :

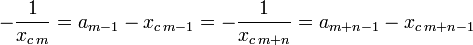
On en déduit que a_m-1 et a_m+n-1 sont tous deux égaux à la partie entière de -1/x_cm et ils sont égaux. Ceci permet de déduire que x_m-1 et x_m+n-1 le sont aussi car leurs conjugués le sont :

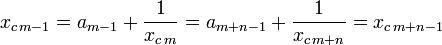
Le fait que a_m-1 et a_m+n-1 soient égaux et que x_m-1 et x_m+n-1 le soient aussi montre que m n'est pas le premier terme de la partie périodique de la suite (a_j). Ceci termine la démonstration.

• Si p est un entier sans facteur carré, la période de la fraction continue de √p démarre au deuxième terme et le dernier terme de la période est égal à 2a₀ :

Soit a₀ le coefficient d'indice 0 de la fraction continue de √p. Le nombre quadratique a₀ + √p possède un développement périodique pure d'après la proposition précédente. Il est en effet strictement plus grand que 1 et son conjugué, égal à a₀ - √p, est compris entre -1 et 0. Pour s'en persuader, il suffit de remarquer que a₀ est la partie entière de √p.

Le premier terme de la fraction continue de a₀ + √p est égal à la partie entière de ce nombre ou encore à 2a₀. Il suffit de remarquer, pour conclure, que √p possède le même développement en fraction continue, à l'exception du premier terme, égal à a₀ et non à 2a₀.

• Si x est la racine carrée d'un entier sans facteur carré, sa fraction continue prend la forme suivante :

Pour une raison de simplicité, la démonstration consiste à étudier la structure de la période de x + a₀. Dans le cas où p est égal à 19, on trouve :

La liste des quotients complets, notés ici x_i est :

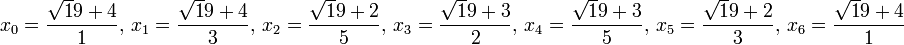
Ce qui permet d'imaginer le résultat suivant :

(1) Il existe deux entiers strictement positifs b_i et c_i tel que x_i = (√p + b_i)/c_i tel que b_i² est strictement plus petit que p et c_i divise p - b_i² :

Montrons cette proposition par récurrence. Pour i égal à 1, on a :

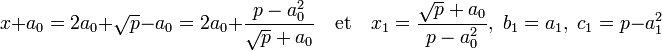
Supposons la propriété vrai à l'ordre i et montrons là à l'ordre i + 1 :

On définit a_i+1 comme la partie entière de x_i et b_i+1 égal à a_i+1.c_i - b_i. L'entier a_i+1 est défini comme la partie entière d'un nombre strictement plus grand que 1, il est donc strictement positif. Montrons que b_i+1 est aussi strictement positif. b_i est strictement plus petit que √p, par hypothèse de récurrence, donc b_i/c_i est strictement plus petit que la moitié de x_i et donc que sa partie entière a_i+1, ce qui revient exactement à dire que b_i+1 est strictement positif. Il ne reste plus qu'à montrer que c_i+1 divise p - b_i+1² :

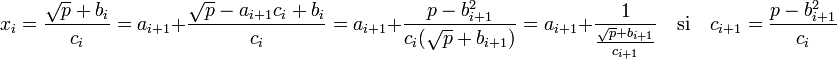
Par construction b_i+1 est un entier de carré strictement plus petit que p, pour montrer le reste de la proposition, il suffit de montrer que c_i divise p - b_i+1². Cette propriété est la conséquence du fait que c_i divise p - b_i² et de l'égalité suivante :

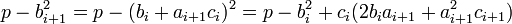
On remarque que les coefficients b_i et c_i forment aussi deux palindromes sur l'exemple √19 choisi. Cette propriété est encore générale et découle de la propriété suivante :

(2) Si i est un entier strictement supérieur à 1, la partie entière du nombre quadratique (√p + b_i)/c_i-1 est égal à a_i-1 et son premier quotient complet à (√p + b_i-1)/c_i-2 :

Dans un premier temps, on remarque que c_i-1 est bien un diviseur de p - b_i², la démonstration précédente montre en effet que p - b_i² est égal à c_i-1.c_i. L'égalité suivante montre que la partie entière de (√p + b_i)/c_i-1 est égal à a_i-1 :

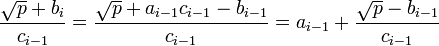
La première démonstration montre que (√p - b_i)/c_i-1 égal à l'opposé du conjugué de x_i-1 est bien un nombre strictement compris entre 0 et 1. Montrons ensuite que le premier quotient complet est bien égal à (√p + b_i-1)/c_i-2 :

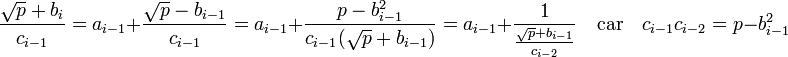
(3) Il existe deux entiers i et j strictement positifs, tel que x_i et x_i+j sont en correspondance. La première valeur possible pour i est (n+1)/2 et pour j : 1 si la période n est impaire et n/2 pour i et 2 pour j sinon :

On remarque que x₁ et x_n+1 sont en correspondance, cette propriété est donc vérifiée pour au moins un couple de quotients complets. Montrons que si x_i et x_i+j sont en correspondance et que j est strictement plus grand que 1, alors x_i+1 et x_i+j-1 sont aussi en correspondance. Le quotient complet précédent x_i+j est égal au premier quotient complet de (√p + b_i+j)/c_i+j-1), c'est-à-dire au premier quotient complet de x_i, d'après la proposition précédente.

On remarque alors que x₁ et x_n+1 sont en correspondance de même que x₂ et x_n et en remontant de proche en proche, x_(n-1)/2 et x_(n+1)/2 sont aussi en correspondance si n est impair. Cette configuration est celle de l'exemple p = 19. La propriété de palindrome est alors établi. Si n est impair, le même raisonnement montre que x_n/2 et x_{n/2 +2} sont en correspondance, il reste encore à vérifier l'égalité entre a_n/2 et a_{n/2 +1}.

(4) Si n est impair, a_(n-1)/2 et a_(n+1)/2 sont égaux :

Cette configuration se produit par exemple pour 13:

La liste des quotients complets est :

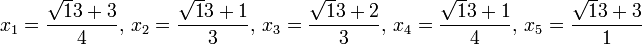
Le raisonnement précédent montre que a₁ est égal à a₄, il faut encore montrer que a₂ est égal à a₃. L'étape (4) permet de conclure. Le quotient complet x_n/2 est égal à (√p + b_{n/2 +2})/c_{n/2 + 1} sa partie entière est donc égal à a_{n/2 + 1}, c'est-à-dire au coefficient d'indice suivant, ce qui termine la démonstration.