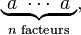Groupe (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Groupes finis
Un groupe est dit fini s'il possède un nombre fini d'éléments. Le nombre de ses éléments est appelé l'ordre de ce groupe. Les groupes symétriques SN, groupes des permutations de N lettres, sont particulièrement importants. Par exemple, le groupe symétrique sur 3 lettres (en) ABC contient les six permutations des trois lettres : ABC, ACB, BAC, BCA, CAB et CBA. Ces groupes sont importants car tout groupe fini est isomorphe à un sous-groupe d'un groupe symétrique SN, pour une certaine valeur de N (théorème de Cayley). De manière analogue au groupe des symétries du carré vu plus haut, S3 peut être vu comme le groupe des symétries d'un triangle équilatéral.
L'ordre d'un élément a d'un groupe G est le plus petit entier positif n tel que an = e, où an représente
c'est-à-dire la répétition de l'opération • sur n copies de a. Dans un groupe infini, un tel ordre n peut ne pas exister, dans ce cas on dit que l'ordre de a est l'infini. L'ordre d'un élément est égal à l'ordre du groupe cyclique engendré par cet élément.
Des techniques de comptage plus sophistiquées produisent des informations plus précises sur les groupes finis : le théorème de Lagrange indique que, pour un groupe fini G, l'ordre de tous sous-groupe H de G divise l'ordre de G. Les théorèmes de Sylow donnent des réciproques partielles.
Le groupe diédral D4 est un groupe fini d'ordre 8. L'ordre de r1 est 4, de même que l'ordre du sous-groupe R engendré par cette rotation. L'ordre des réflexions fv etc, est 2. Ces ordres divisent 8, comme l'indique le théorème de Lagrange.
Classification des groupes simples finis
La classification des groupes finis mène rapidement à des mathématiques profondes et difficiles. D'après le théorème de Lagrange, les groupes finis d'ordre p, où p est un nombre premier, sont nécessairement cycliques, abéliens et isomorphes à Zp. On peut également montrer que les groupes d'ordre p2 sont abéliens. Ce résultat ne se généralise pas à p3, comme le montre le groupe diédral D4 non abélien d'ordre 8 = 23. Un système de calcul formel peut être utilisé pour établir une liste des petits groupes, mais il n'existe aucune classification de tous les groupes finis.
Une étape intermédiaire est la classification des groupes simples finis. Un groupe non trivial G est dit simple si ses seuls sous-groupes normaux sont le groupe trivial (réduit à l'élément neutre simple) et le groupe G lui-même. Le théorème de Jordan-Hölder désigne les groupes simples comme étant les « briques » utilisées pour construire tous les groupes finis. L'élaboration de la liste des groupes finis simples fut un résultat majeur de la théorie des groupes contemporaine. Richard Borcherds, lauréat de la médaille Fields en 1998, parvint à prouver les conjectures monstrous moonshine, une relation surprenante et profonde entre le plus grand groupe sporadique fini simple (le groupe Monstre) et certaines formes modulaires, qui font partie de l'analyse complexe et de la théorie des cordes, une théorie supposée unifier la description de nombreux phénomènes physiques.
Généralisations
| Structures algébriques semblables aux groupes | ||||
| Totalité | Associativité | Élt neutre | Inverse | |
|---|---|---|---|---|
| Groupe |
|
|
|
|
| Monoïde |
|
|
|
|
| Demi-groupe |
|
|
|
|
| Boucle |
|
|
|
|
| Quasigroupe |
|
|
|
|
| Magma |
|
|
|
|
| Groupoïde |
|
|
|
|
| Catégorie |
|
|
|
|
En algèbre générale, des structures plus générales sont définies en omettant certains axiomes de la définition des groupes. Par exemple, si la condition que chaque élément possède un inverse est éliminée, on obtient une structure algébrique appelée monoïde. Les nombres entiers naturels N, munis de l'addition, forment un monoïde, de même que l'ensemble des entiers relatifs non nuls munis de la multiplication (Z \ {0}, ·) vu plus haut. Il existe une méthode générale pour ajouter de façon formelle des inverses aux éléments d'un monoïde commutatif, de façon analogue à celle dont (Q \ {0}, ·) est dérivé de (Z \ {0}, ·). Le groupe ainsi obtenu est appelé groupe de Grothendieck (en) du monoïde.
Un groupoïde est semblable à un groupe, si ce n'est que la loi a • b n'est pas définie pour tous les éléments a et b. Les groupoïdes apparaissent dans l'étude de formes plus compliquées de symétries, souvent dans les structures topologiques ou analytiques, comme le groupoïde fondamental. Le tableau ci-contre donne différentes structures généralisant celle de groupe.
il existe 129 groupoides commutatifs à 5 éléments; mais comment les construire?