Groupe (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Concepts essentiels
Pour comprendre les groupes au-delà des manipulations symboliques présentées ci-dessus, d'autres concepts doivent être employés. Ils suivent tous un principe sous-jacent : pour bénéficier de la structure de groupe, les constructions liées à un groupe doivent être "compatibles" avec sa loi de composition. Cette compatibilité se manifeste de différentes façons. Par exemple, des groupes peuvent être reliés entre eux par des fonctions appelées homomorphismes de groupe, c'est-à-dire des fonctions qui conservent la structure de groupe. La structure des groupes peut aussi être étudiée en les "cassant" en morceaux plus simples, appelés sous-groupes ou groupes quotients. Ce principe de conservation des structures est l'idée centrale de la théorie des catégories, dans laquelle on parle de catégorie des groupes.
Homomorphisme de groupe
Les homomorphismes de groupes sont les fonctions qui préservent la structure de groupe. Une fonction f : G → H entre deux groupes munis respectivement de deux lois • et * est un homomorphisme si l'égalité
- f(a • b) = f(a) * f(b).
est vraie pour tous les éléments a et b de G, c'est-à-dire que le résultat est le même, que l'on effectue l'opération avant ou après avoir appliqué la fonction f.
Cette condition assure que l'image de l'inverse de tout élément a est l'inverse de l'image de a. En notant a—1 l'inverse d'un élément a, cela donne :
- f(a—1) = f(a)—1
et que l'image de l'élément neutre du groupe (G ; •) est l'élément neutre de (H ; *).
Ainsi l'image d'un homomorphisme de groupe respecte les axiomes de groupe.
Notons eG et eH respectivement les éléments neutres des groupes G et H.
Quel que soit l'élément a de G,
- f(a • eG) = f(a) * f(eG).
Or, a • eG = a, donc
- f(a • eG) = f(a).
Par conséquent, quel que soit a dans G,
- f(a) = f(a) * f(eG).
En appliquant f(a)—1 à gauche,
- f(a)—1 * f(a) = f(a)—1*f(a) * f(eG)
soit (en utilisant le fait que f(a)—1*f(a) = eH) :
- eH = f(eG)
Donc f(eG) est élément neutre de H.
D'autre part, la définition d'un homomorphisme donne, quel que soit a dans G :
- f(a • a—1) = f(a) * f(a—1)
c'est-à-dire :
- f(eG) = f(a) * f(a—1)
- eH = f(a) * f(a—1)
ce qui montre que f(a—1) est l'inverse de f(a).
Deux groupes G et H sont dits isomorphes s'il existe deux homomorphismes de groupes f : G → H et g : H → G tels que la composée de ces deux fonctions, quel que soit l'ordre, donne l'identité. C'est-à-dire que, quels que soient a élément de G et b de H,
- g(f(a)) = a et
- f(g(b)) = b.
Du point de vue de la structure de groupe, G et H sont en quelque sorte "le même groupe".
Sous-groupe
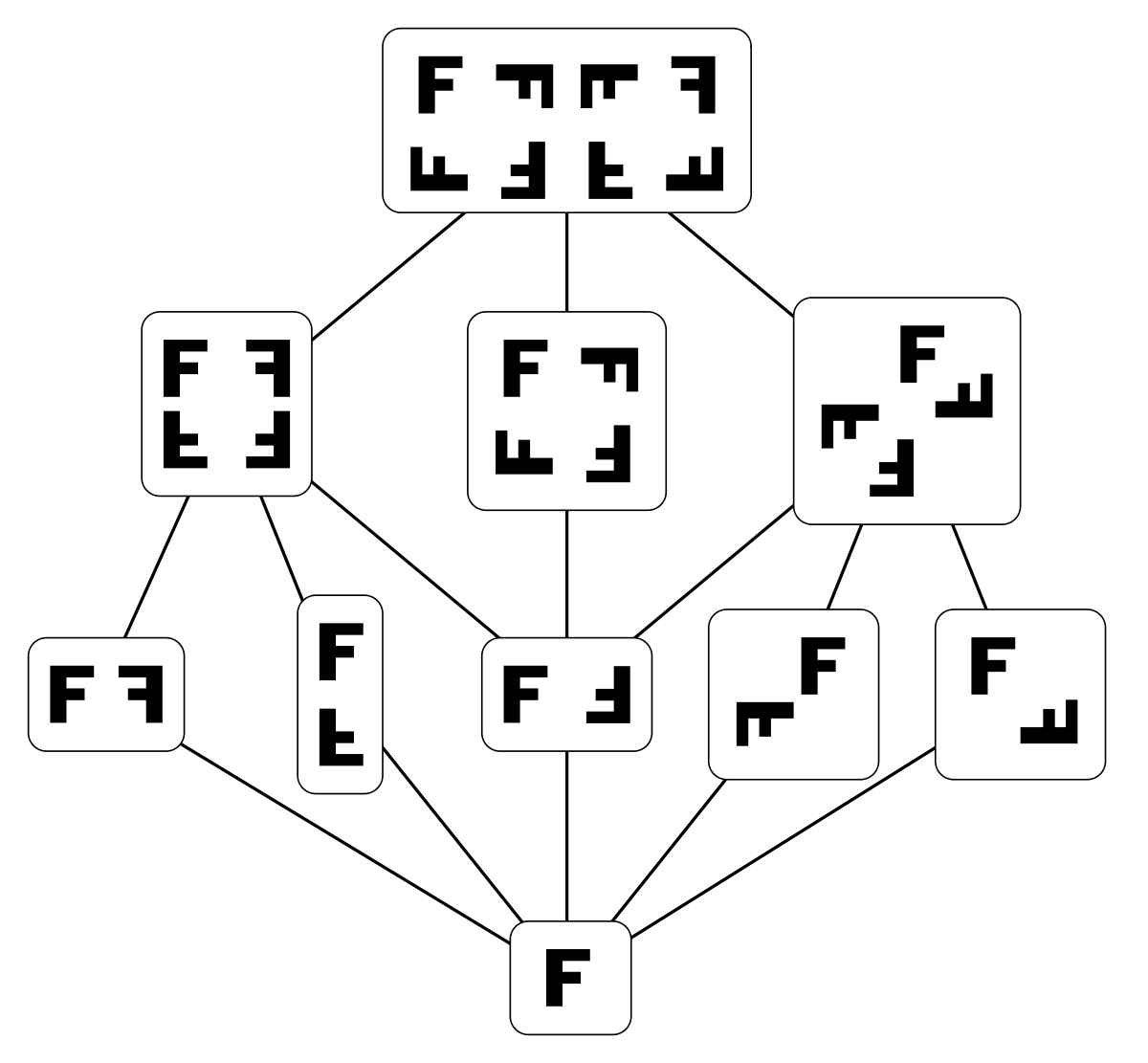
Intuitivement, un sous-groupe est un groupe H inclus dans un autre groupe G. Cela signifie que l'élément neutre de G est contenu dans H et, quels que soient h1 et h2 éléments de H, h1 • h2 et h1−1 appartiennent aussi à H.
Dans l'exemple du groupe D4 ci-dessus, l'identité et les rotations forment un sous-groupe R = {id, r1, r2, r3} coloré en rouge dans le tableau : la composée de deux rotations est une rotation et chaque rotation a pour inverse une rotation, celle telle que la somme des angles des deux rotations est 360° (un tour complet).
Une condition nécessaire et suffisante pour qu'un sous-ensemble H d'un groupe G soit un sous-groupe de G est que, quels que soient les éléments a et b de H :
- a−1 • b ∈ H.
La connaissance du treillis des sous-groupes d'un groupe donné est importante pour la compréhension de ce groupe.
Étant donné un sous-ensemble S d'un groupe G, le sous-groupe engendré par S est constitué par tous les produits des éléments de S avec des inverses de ces éléments, l'opération pouvant être répétée plusieurs fois. C'est le plus petit sous-groupe contenant S. Dans l'exemple D4, le sous-groupe engendré par r2 et fv est constitué de ces deux éléments, de l'identité et de fh = fv • r2. C'est un sous-groupe, car combiner deux éléments, ou leurs inverses donne un élément de cet ensemble. On peut également remarquer que le groupe (Z ; +) des entiers relatifs est engendré par le seul élément 1 : on peut obtenir n'importe quel entier en ajoutant 1 avec lui même ou avec son opposé —1. On dit que Z est monogène. Le sous-groupe de Z engendré par 2 est constitué des nombres pairs (noté 2Z), celui qui est engendré par 3 est le sous-groupe des multiples de 3 (noté 3Z), etc.
Classe suivant un sous-groupe
Dans de nombreuses situations, il est souhaitable de considérer que deux éléments d'un groupe sont les mêmes s'ils diffèrent d'un élément d'un sous-groupe donné.
Par exemple, dans D4, une fois qu'un retournement a été effectué, le carré ne peut jamais revenir à la position de r2 par application de rotations, sans autre retournement. Il est possible de classer les figures du carré données dans l'exemple ci-dessus suivant deux parties : celle qui rassemble les figures pour lesquelles la suite des sommets 1-2-3-4 est parcourue dans le sens des aiguilles d'une montre, et celle des figures où 1-2-3-4 est parcouru dans l'autre sens. Il est possible de passer d'une figure d'une de ces parties à une autre par un retournement, mais aucune rotation ne permet de passer d'un carré de type « 1-2-3-4 dans le sens des aiguilles d'une montre » à un carré de l'autre type. Ainsi, deux figures du même type diffèrent d'une rotation.
La notion de classe suivant un sous-groupe formalise ceci : un sous-groupe H définit une classe à gauche et une classe à droite, qui peuvent être vues comme des translations de H par des éléments arbitraires g du groupe. Les classe à gauche et classe à droite suivant H contenant g sont respectivement
- gH = {g • h, h ∈ H} et Hg = {h • g, h ∈ H},
c'est-à-dire les ensembles constitués de tous les éléments de la forme g • h (classe à gauche) et de la forme h • g (classe à droite), où h est un élément de H.
Les classes suivant un sous-groupe H forment une partition de G, c'est-à-dire que la réunion de toutes les classes à gauche est égale à G et l'intersection de deux classes à gauche différentes est vide.
L'égalité g1H = g2H a lieu si et seulement si g1−1g2 ∈ H, c'est-à-dire lorsque g1 et g2 diffèrent d'un élément de H. De même pour les classes à droite suivant H. Les classes à gauche et à droite suivant H peuvent être égales, mais ce n'est pas le cas en général. Si, pour tout élément g de G, gH = Hg, alors H est un sous-groupe normal (ou distingué) de G.
Dans D4, les classes à gauche gR relatives au sous-groupe R constitué par les rotations sont : soit R si g est une rotation, soit l'ensemble U = fvR = {fv, fd, fh, fc} colorié en vert sur la table de Cayley donnée plus haut. Le sous-groupe R est distingué car les classes à gauche et à droite sont égales : fvR = U = Rfv, par exemple, cette égalité étant aussi vraie pour tous les éléments autres que fv.
Dans Z, le sous groupe 2Z des nombres pairs définit deux classes : celle des nombres pairs et celle des nombres impairs. Les classes à gauche et à droite dans Z sont toujours égales car ce groupe est commutatif.
Groupe quotient
Lorsqu'un sous-groupe est distingué, l'ensemble des classes qu'il définit forme également un groupe, appelé groupe quotient de G par N et noté G / N.
- G / N = {gN, g ∈ G}
L'opération de ce nouveau groupe est induite par celle de G :
- (gN) • (hN) = (g • h)N
pour tous éléments g et h de G. Cette étude est motivée par l'idée que l'application G → G / N qui, à tout élément g du groupe associée sa classe gN, est un homomorphisme de groupe. La classe eN = N est l'élément neutre du groupe quotient et l'inverse de gN est (gN)−1 = (g−1)N.
| • | R | U |
|---|---|---|
| R | R | U |
| U | U | R |
| Table du groupe quotient D4 / R. | ||
Les éléments du goupe quotient D4 / R sont R lui-même, qui repésente l'élément neutre, et U = fvR. La loi de groupe de ce quotient est représentée dans le tableau ci-contre. Par exemple, U • U = fvR • fvR = (fv • fv)R = R. Le sous-groupe R = {id, r1, r2, r3} et le groupe quotient correspondant sont tous les deux commutatifs, alors que D4 ne l'est pas. L'idée de construire de grands groupes à partir d'autres plus petits est formalisée par la notion de produit semi-direct.
Le quotient et les sous-groupes permettent de décrire tout groupe par sa présentation : chaque groupe est le quotient du groupe libre sur l'ensemble de ses générateurs, quotienté par le sous-groupe des relations. Le groupe dihédral D4, par exemple, peut-être engendré par deux éléments r et f, où r est une rotation et f un retournement quelconques par exemple r1 (rotation d'angle droit) et fv (retournement vertical). Cela signifie que toute symétrie du carré est une composition finie de ses deux symétries et de leurs inverses. Ceci, avec les relations
- r 4 = f 2 = (rf)2 = 1,
décrit complètement le groupe. Une présentation d'un groupe peut aussi servir à construire le graphe de Cayley, un outil utilisé pour représenter graphiquement les groupes discrets.
Les sous-groupes et groupes quotients sont liés par la relation suivante : un sous-ensemble H de G peut être vu comme une injection H → G, c'est-à-dire que chaque élément de G possède au plus un antécédent par cette fonction. La notion d'application injective est liée avec celle d'application surjective (une application pour laquelle tout élément de l'ensemble d'arrivée admet au moins un antécédent). L'application canonique G → G / N est surjective. Les théorèmes d'isomorphisme permettent d'exhiber des homomorphismes injectifs, surjectifs et bijectifs « naturels » d'un groupe afin de comprendre sa structure.

















































