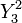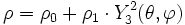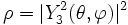Harmonique sphérique - Définition

Représentations graphiques

Représentation sphérique

Si l'on utilise la représentation sphérique

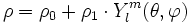
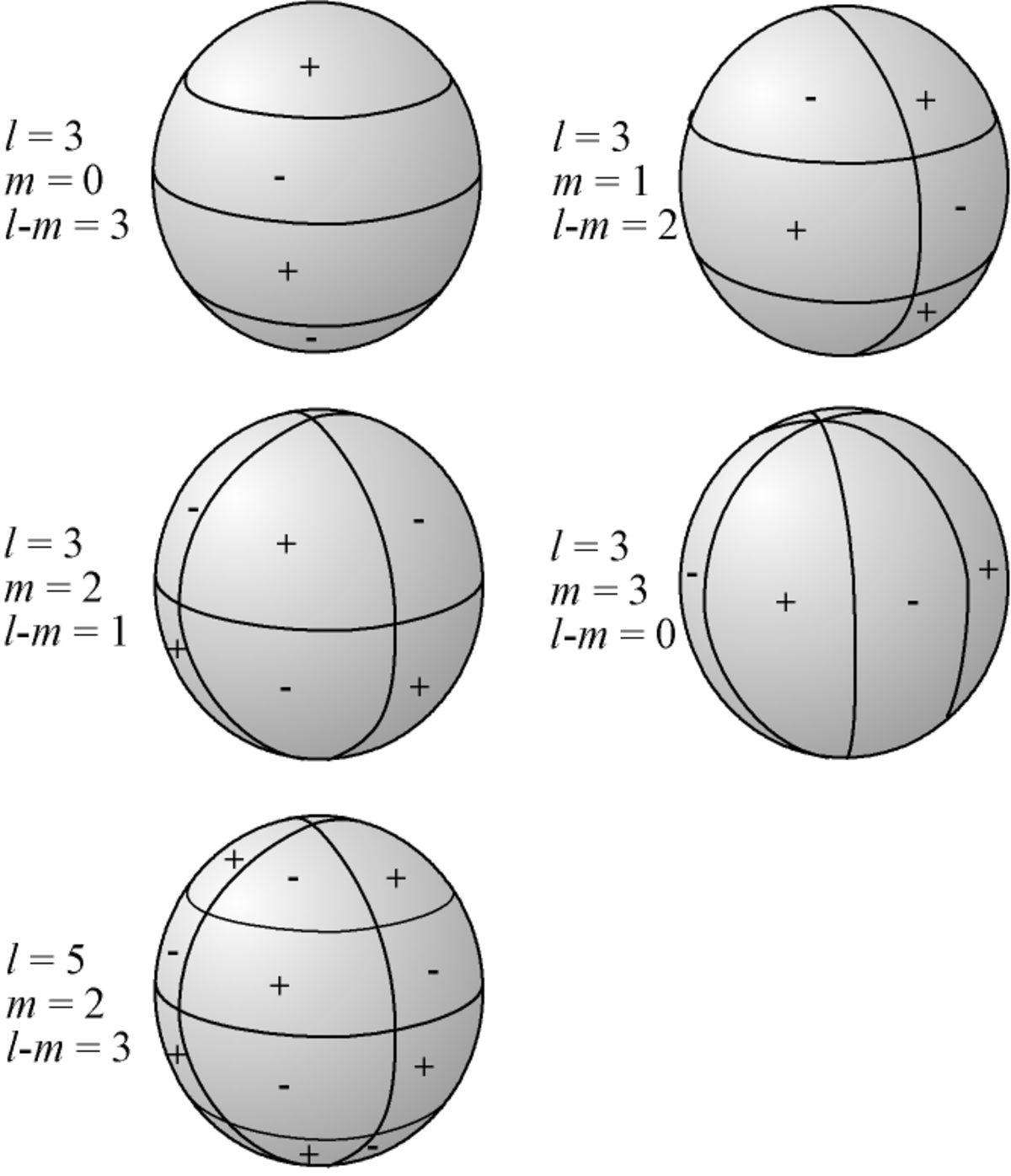
alors la surface représentatrice est une sphère bosselée ; les bosses correspondent aux parties où Y_l^m est positif, les creux aux parties où Y_l^m est négatif. Lorsque θ et décrivent l'intervalle [0;2π[, Y_l^m(θ, φ) s'annule selon l cercles :

• m cercles suivant un méridien, une iso-longitude (intersection entre un plan contenant Oz et la sphère) ;
• l − m cercles suivant un parallèle, une iso-latitude (intersection entre un plan parallèle à Oxy et la sphère).

Le paramètre l est appelé le « degré », m est appelé l'« ordre azimutal ». Entre les cercles d'annulation, la fonction est alternativement positive ou négative.

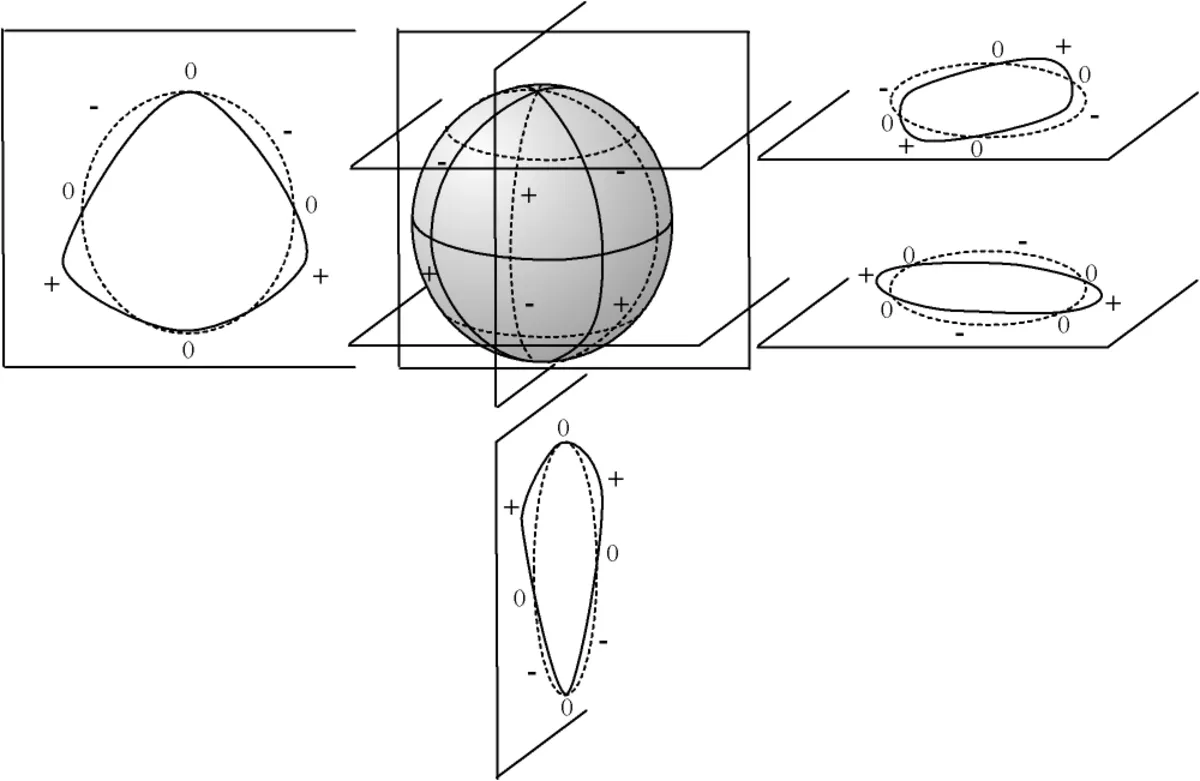
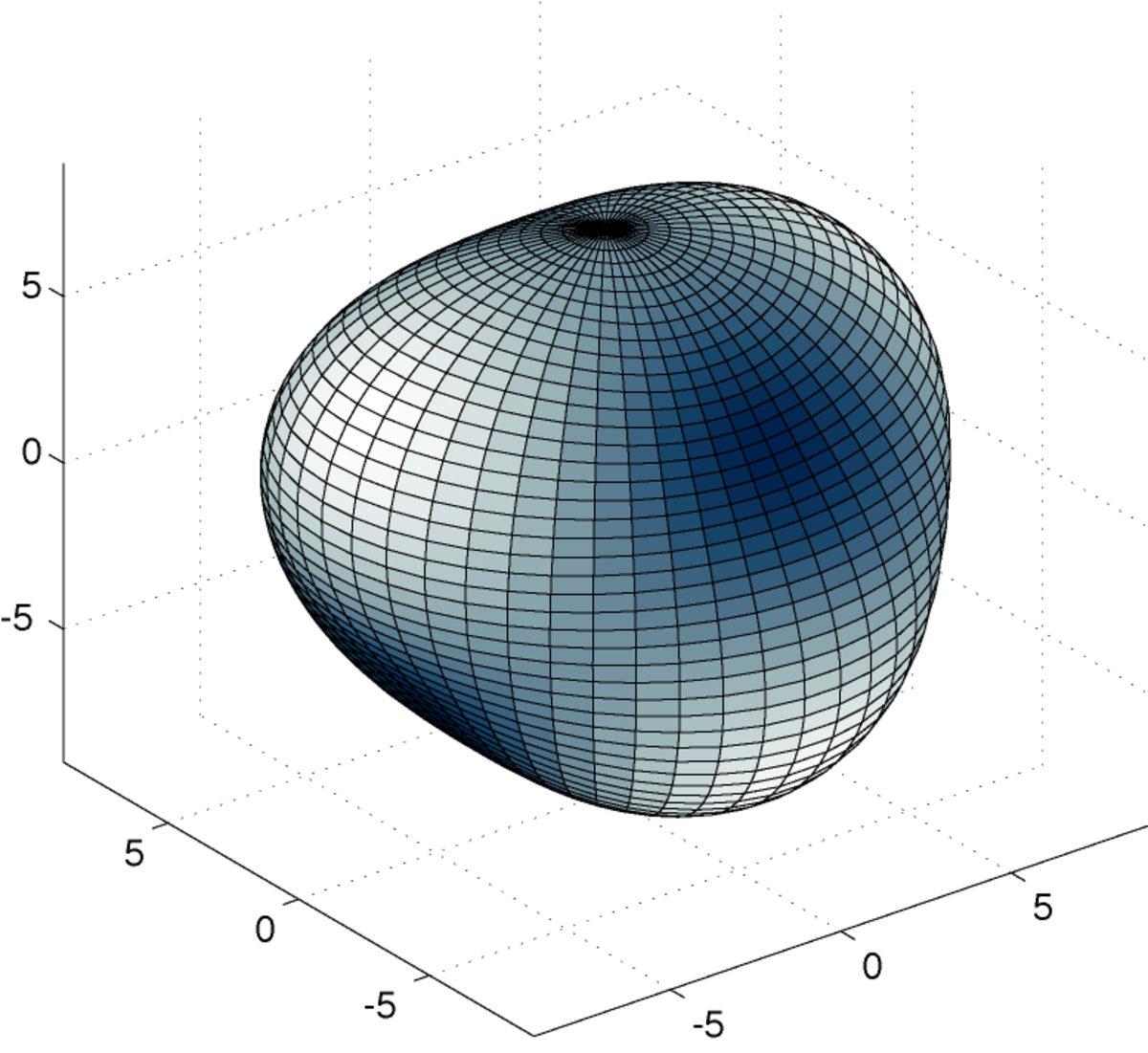
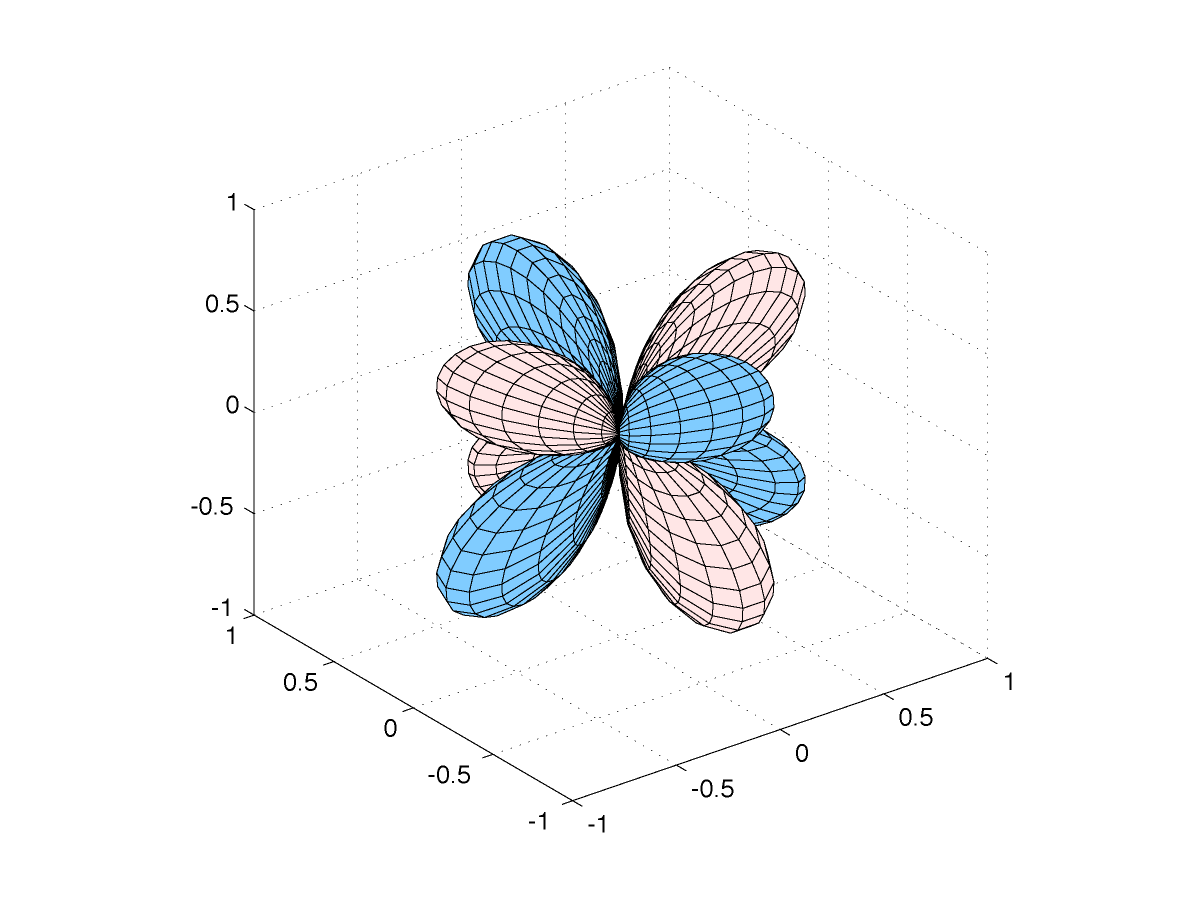
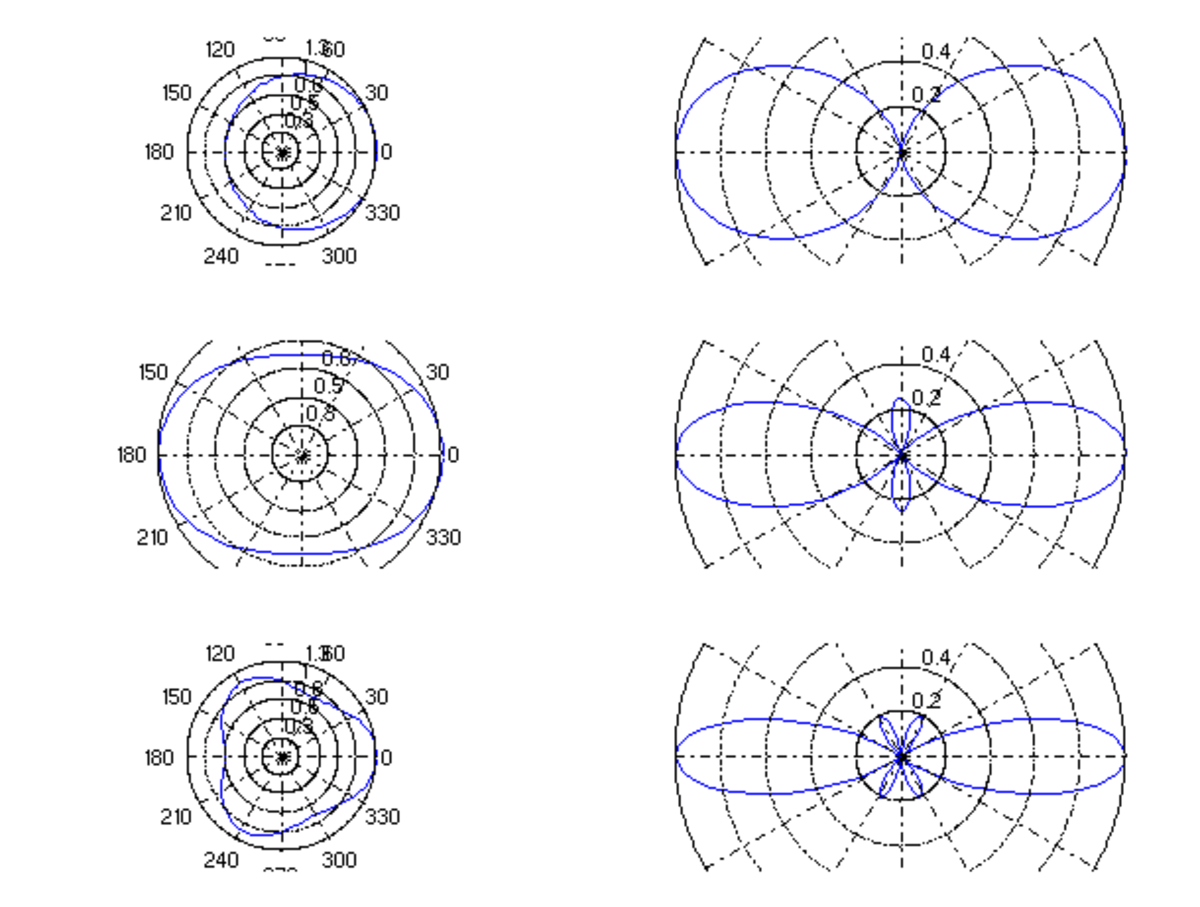
Nous représentons ci-dessous quatre coupes de l'harmonique sphérique Y₃² :

Comme précédemment, on peut représenter la fonction par la courbe en coordonnées sphériques :

Représentation en coupe

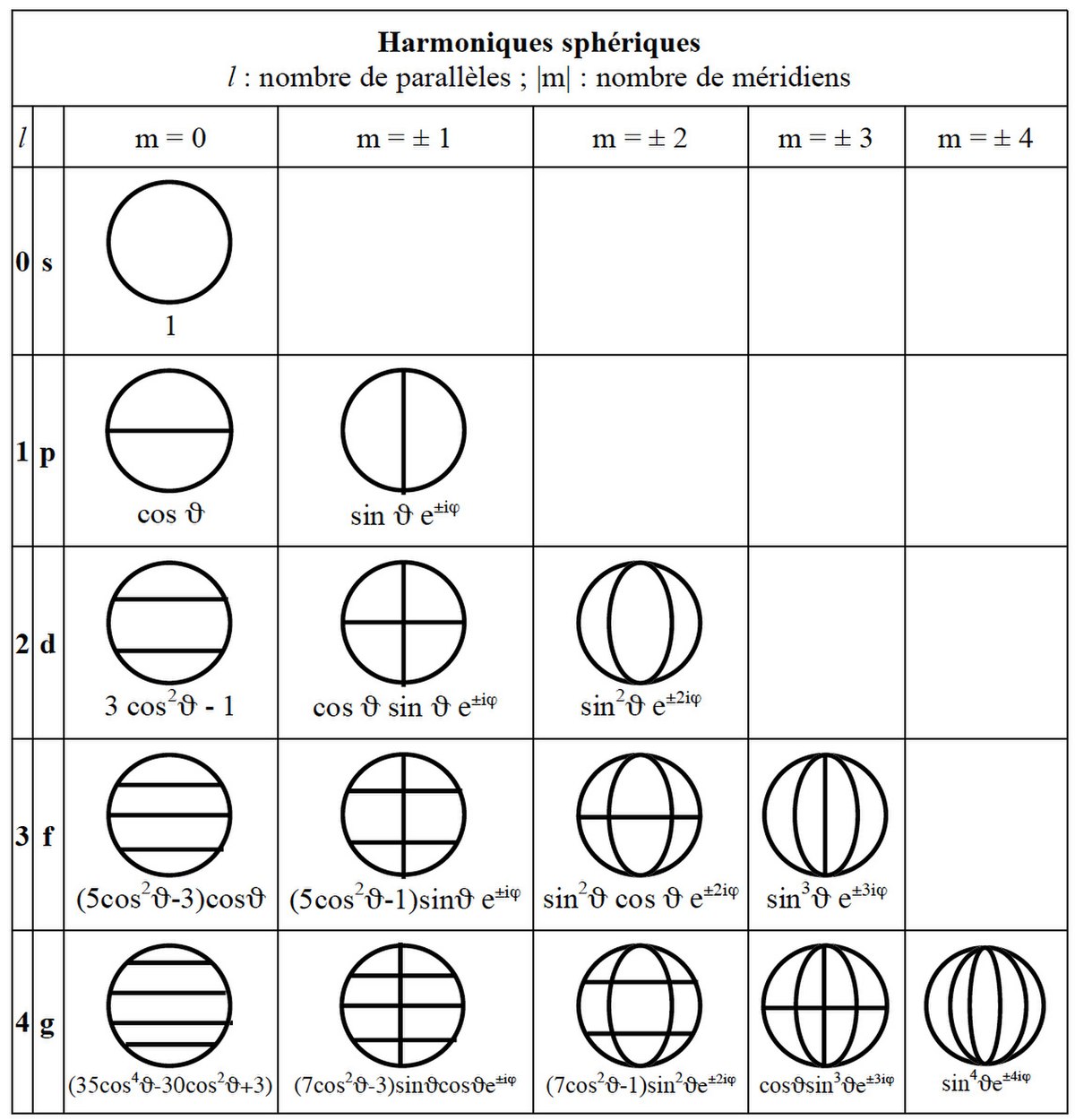
Les harmoniques sphériques peuvent être représentées de façon plus simple sans les ventres de vibration, en ne gardant que les noeuds, comme le montre le tableau suivant. Ce sont les sphères de la figure du haut, projetées sur un plan vertical. On retrouve sur la dernière ligne les quatre sphères de la première figure ci-dessus où l = 3. Les quatre valeurs de m y varient de 0 à 3 en valeur absolue. Sur la figure ci-après, on distingue les valeurs négatives pour tenir compte de ce que la rotation peut se faire dans un sens ou dans l'autre pour m > 0. Pour montrer la concordance avec les harmoniques, leur plus simple expression est donnée sous chaque sphère.

On reconnaît les nombres quantiques secondaire l, correspondant aux sous-couches s, p, d, f et m, magnétique, de l'atome d'hydrogène. Le nombre quantique principal n n'apparaît pas car les modes radiaux sont différents selon le problème étudié, résonance acoustique, atome d'hydrogène ou autre.

Pour montrer la concordance avec la littérature, l’expression des harmoniques sphériques est donnée sous chaque sphère. Le nombre et la valeur des zéros des polynômes de Legendre associés, non normalisés, donne le nombre de parallèles et leur position sur l’axe vertical. L’exponentielle imaginaire exp(imφ), de module unité, utilisée habituellement au lieu des sinus et cosinus, donne le nombre de méridiens. Les valeurs de ne s’observent que dans les états excités ou les atomes de Rydberg où la valeur habituelle de l est 50 et dont l'orbitale est représentée non par une sphère mais par un anneau.

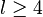
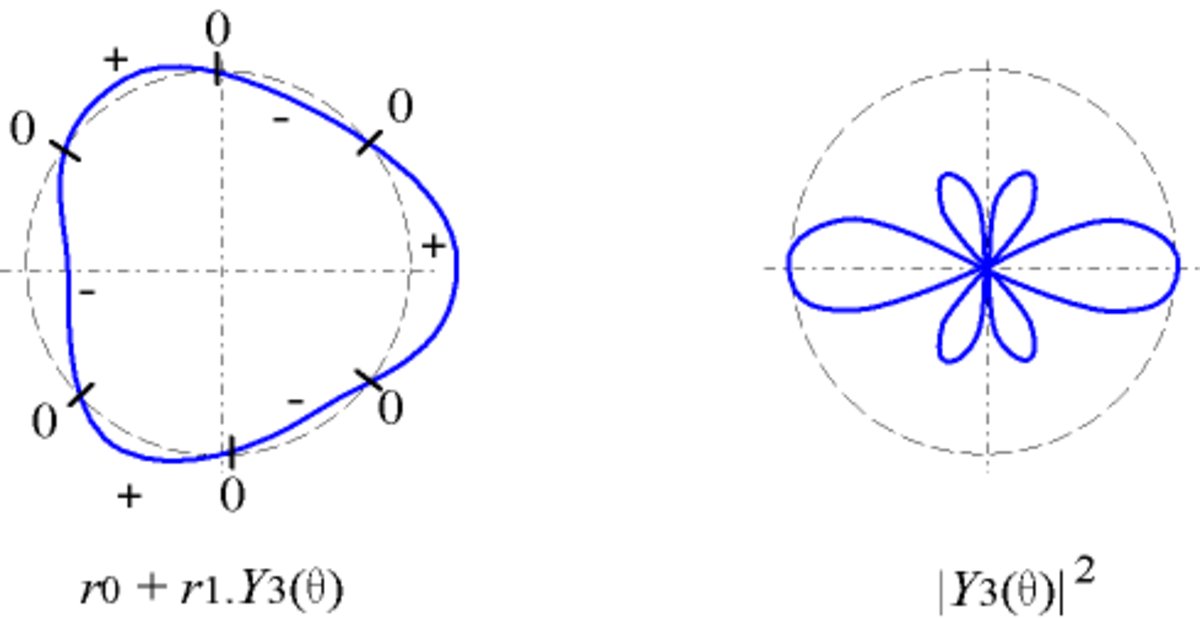
Représentation cartésienne et polaire

On peut représenter les harmoniques circulaires de trois manières :

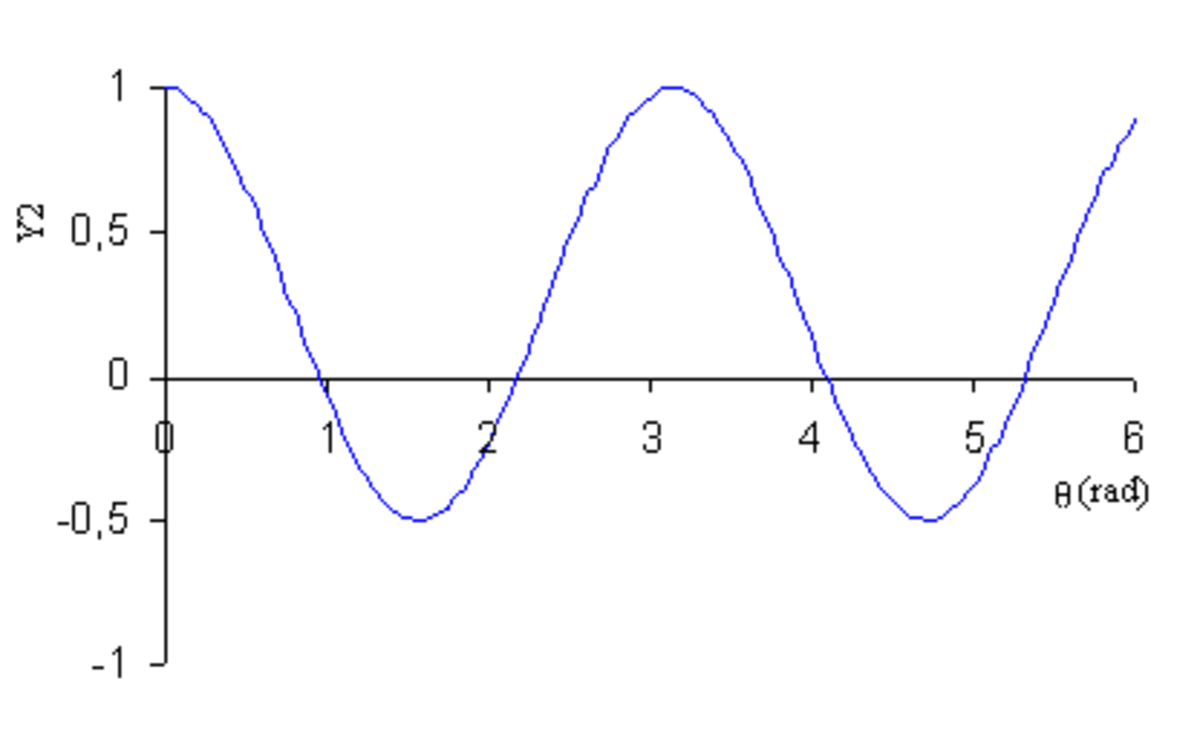
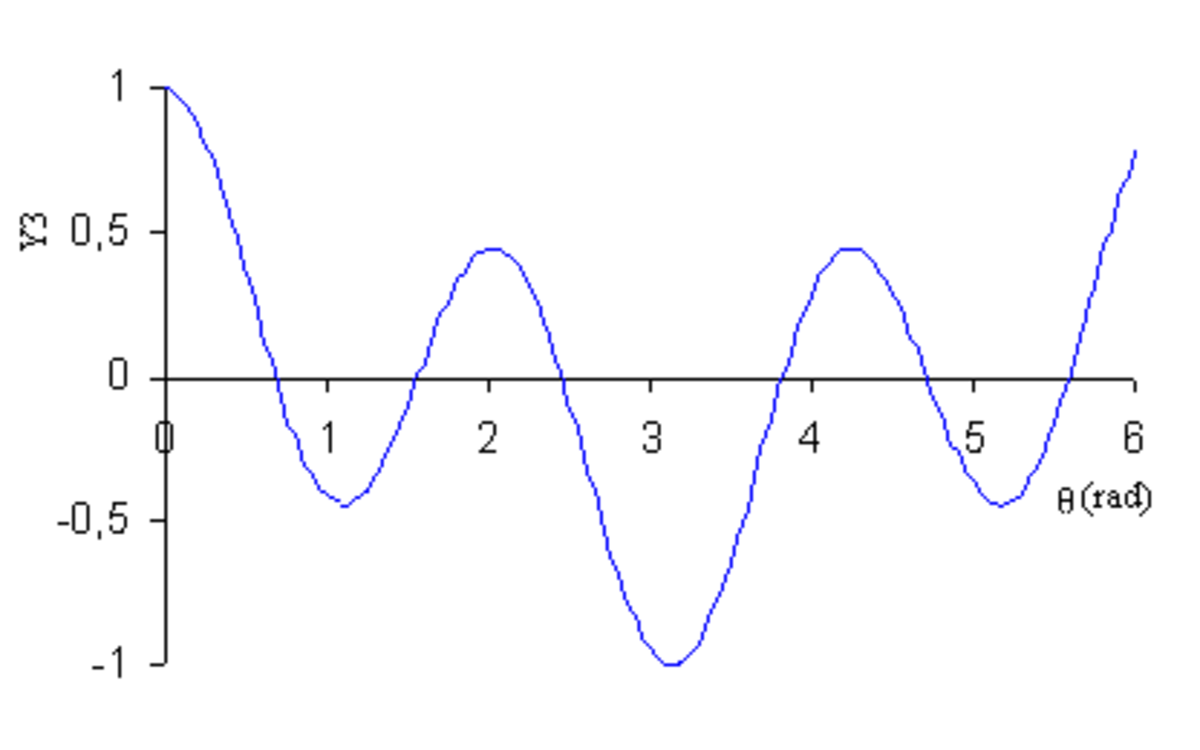
• en coordonnées cartésiennes : y = Y_l(θ) ;
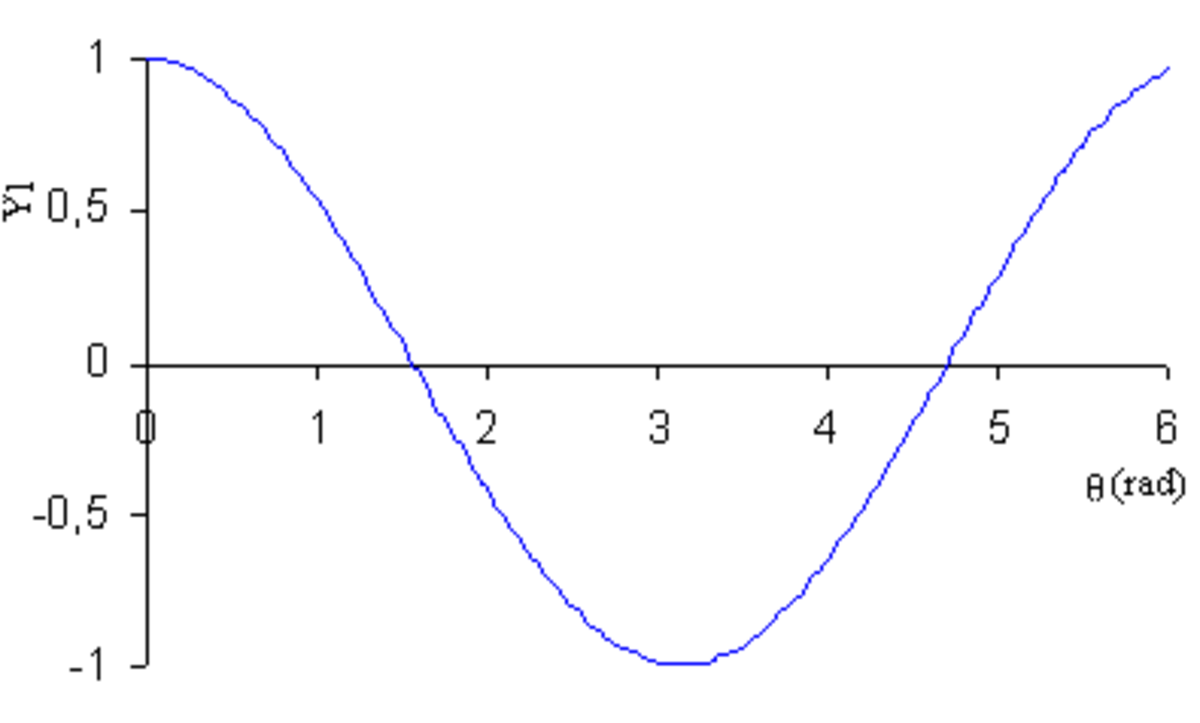
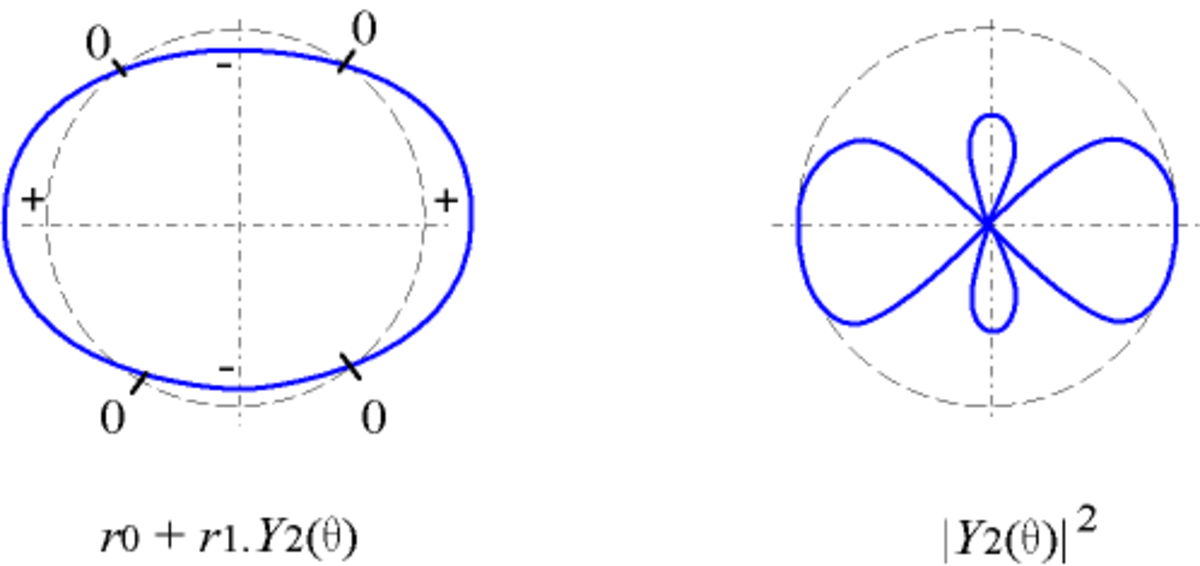
• en coordonnées polaires : r = r₀ + r₁.Y_l(θ)
  avec r₁ < r₀, utilisé par exemple pour un objet circulaire ; la courbe coupe le cercle de centre O et de rayon r₀ lorsque la fonction s'annule ;
• en coordonnées polaires : r = | Y_l(θ) | ²
  utilisé par exemple pour les fonctions d'onde en physique quantique.

Trois premières harmoniques circulaires

	Représentation cartésienne	Représentations polaires (tracé manuel)	Représentations polaires (tracé exact)
Y1
Y2
Y3