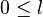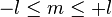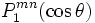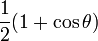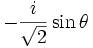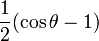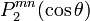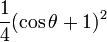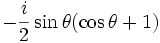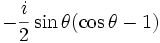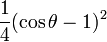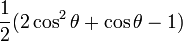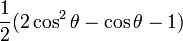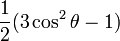Harmonique sphérique - Définition
La liste des auteurs de cet article est disponible ici.
Harmoniques sphériques normalisées
Base orthonormale des harmoniques sphériques
Parmi les (2l + 1) fonctions, l'habitude a été prise de sélectionner une base orthomormale sur la sphère S2 munie de la mesure
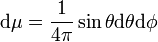
soit le produit scalaire (hermitien en fait) :
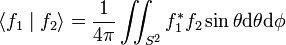
Les harmoniques sphériques sont les solutions de l'équation aux valeurs propres :
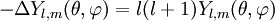
où l'opérateur laplacien s'écrit en coordonnées sphériques sur la sphère de rayon unité, J2 :
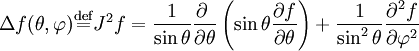
Elles sont fonctions propres de l'opérateur
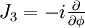
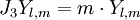
Celles-ci, une fois normées sur la sphère sont alors notées usuellement
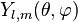
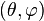
Normalisation
Les harmoniques sphériques constituent une base orthonormale de fonctions propres de l'opérateur laplacien sur la sphère de rayon unité S2 au sens où :
Elles sont orthogonales pour le produit scalaire suivant :
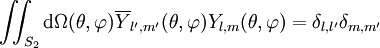
Dans cette formule,
Toute fonction
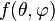
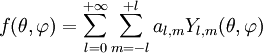
où les coefficients complexes al,m se calculent par :
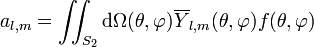
Expression des harmoniques sphériques normalisées
Les harmoniques sphériques généralisées sont définies sur la sphère S3. La normalisation des harmoniques sphériques conduit à l'expression finale :
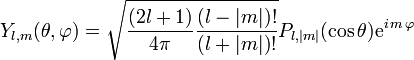
Autres harmoniques
Harmoniques circulaires
Dans le plan, la décomposition s'écrit :
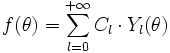
Y0 est une fonction constante, la courbe représentatrice en coordonnées polaires r = Y0(θ) est donc un cercle de rayon r0.
Yl est une fonction invariante par une rotation d'un angle de 1 / (l + 1) tour, c'est-à-dire que
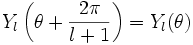
on dit que Yl admet une symétrie d'ordre l + 1.
Harmoniques sphériques généralisées
Lorsque l'on considère l'orientation d'un objet dans l'espace, il faut faire appel à trois angles ; on utilise en général les angles d'Euler (ψ, θ, φ).
Considérons une fonction continue de l'orientation ƒ(ψ, θ, φ) ; comme précédemment, cette fonction peut être décomposée en harmoniques sphériques généralisées
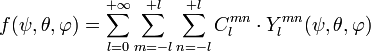
où Clmn est une constante. La fonction Ylmn s'écrit :
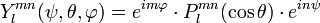
Le polynôme Plmn est le polynôme de Legendre généralisé
![P_l^{m n} (X) = \frac{(-1)^{l-m} \cdot i^{n-m}}{2^l \cdot (l-m)!} \cdot \left [ \frac{(l-m)! (l+n)!}{(l+m)! (l-n)!} \right ]^{1/2} \cdot (1-X)^{-\frac{n-m}{2}}](https://static.techno-science.net/illustration/Definitions/autres/1/158960efc7cffb66e972c877751e722d_ae8f5fa6e7f253dc3f9471566a576fc6.png)
![\cdot (1+X)^{-\frac{n+m}{2}} \cdot \frac{\partial^{l-n}}{\partial X^{l-n}} \left [ (1-X)^{l-m} (1+X)^{l+m} \right ]](https://static.techno-science.net/illustration/Definitions/autres/e/ebf25d1f51fc71afd5af8b3349778383_86c6f35226ec31a9d246ee88c1ab04e1.png)
Quand X décrit l'intervalle [ − 1;1], cette fonction Plmn est soit réelle, soit imaginaire pure. Y000(ψ, θ, φ) est la fonction isotrope (symétrie sphérique).
D'après la loi de composition des rotations, on a :
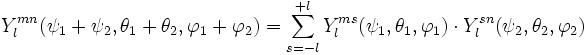
et en particulier
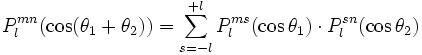
On a de manière générale :
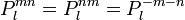
Par exemple pour l = 1 :
| m | n | ||
|---|---|---|---|
| -1 | 0 | +1 | |
| -1 |
|
|
|
| 0 |
| cosθ |
|
| 1 |
|
|
|
Pour l = 2 :
| m | n | ||||
|---|---|---|---|---|---|
| -2 | -1 | 0 | +1 | +2 | |
| -2 |
|
|
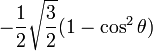
|
|
|
| -1 |
|
|
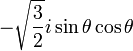
|
|
|
| 0 |
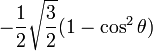
|
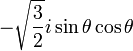
|
|
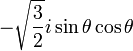
|
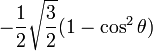
|
| 1 |
|
|
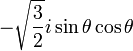
|
|
|
| 2 |
|
|
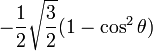
|
|
|