Instabilité de Rayleigh-Taylor - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’instabilité de Rayleigh–Taylor, nommée en hommage aux physiciens britanniques Lord Rayleigh et G. I. Taylor, est une instabilité de l’interface séparant deux fluides de densités différentes, qui résulte de la poussée du fluide le plus lourd sur le fluide le plus léger (l'accélération dans le cas d'un système dynamique ou la gravité pour un système initialement statique est dirigée vers la phase légère). Ce phénomène est produit par exemple par l'onde de choc à l'origine des nuages interstellaires. Dans ce cas particulier où le choc est à l'origine de la mise en vitesse du système, on parlera d'instabilité de Richtmyer-Meshkov. Il se produit une situation analogue lorsque la gravité affecte deux fluides de densités différentes (le fluide le plus dense se trouvant au-dessus du fluide le moins dense) comme de l'huile minérale à la surface de l'eau.
Considérons deux couches de fluides immiscibles superposées dans deux plans parallèles, la plus lourde surplombant la plus légère et toutes deux soumises à la pesanteur terrestre. L’équilibre est instable à la moindre perturbation : toute perturbation va s'amplifier et libérer de l’énergie potentielle, le fluide le plus lourd gagnant progressivement la moitié inférieure sous l'effet du champ de gravitation, et le fluide léger passe au-dessus. C'est cette configuration qu'a étudiée Lord Rayleigh. La découverte importante de G. I. Taylor a consisté à montrer que cette situation est équivalente à celle qui se produit lorsque les fluides (hors de toute gravité) sont accélérés, le fluide léger étant propulsé à l'intérieur du fluide le plus lourd. Cela se produit notamment lorsque l'on projette un verre à terre avec une accélération supérieure à la pesanteur terrestre g.
Lorsque l’instabilité développe ses effets, des irrégularités (« fossettes ») se propagent vers le bas en polypes de Rayleigh–Taylor qui finissent même par se mélanger. C'est pourquoi on qualifie parfois l’instabilité de Rayleigh–Taylor d’instabilité à traines (fingering instability). Le fluide le plus léger s'expand vers le haut comme un champignon nucléaire.
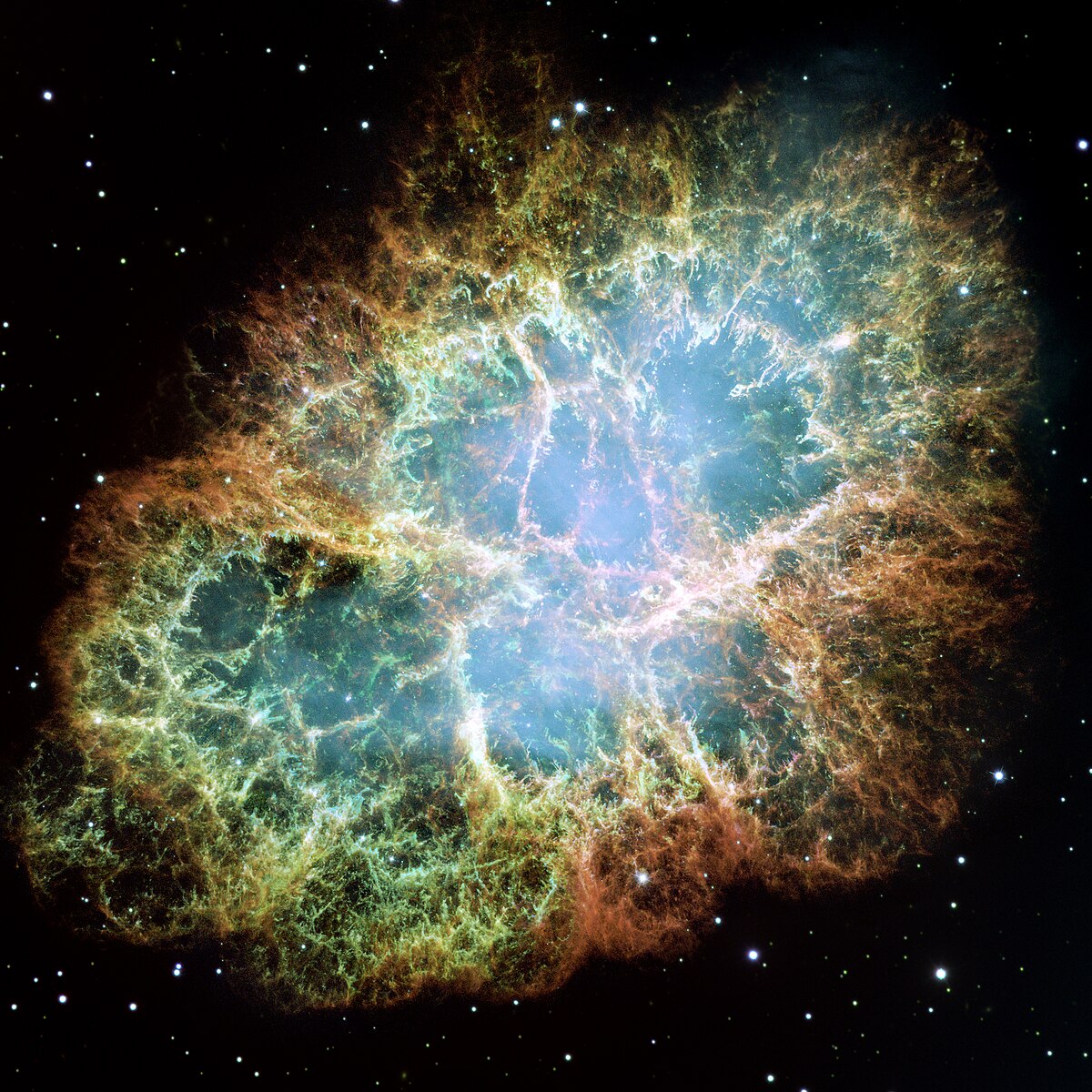
On observe ce phénomène dans plusieurs situations courantes, non seulement dans les dômes salins ou les couches d’inversion, mais aussi en astrophysique et en électrocinétique. Les polypes de Rayleigh-Taylor sont particulièrement visibles dans la Nébuleuse du Crabe, où le plérion engendré par le pulsar du Crabe déborde les projections issues de l’explosion de la supernova il y a 1 000 ans.
Il ne faut pas confondre l’instabilité de Rayleigh–Taylor avec l’instabilité de Plateau-Rayleigh (parfois appelée « instabilité du tuyau d'arrosage ») : cette dernière, qui se produit dans les jets de liquide, est due à la tension superficielle, qui tend à disperser un jet cylindrique en une projection de gouttelettes de même volume mais de surface spécifique moindre.
Analyse linéaire de la stabilité
L’instabilité bidimensionnelle non-visqueuse de Rayleigh–Taylor constitue un excellent banc d'essai pour l'étude mathématique de la stabilité du fait de la nature extrêmement simple de la configuration initiale, décrite par un champ de vitesse moyenne tel que
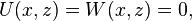
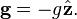
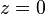
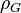
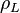
où
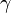

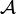
La perturbation apportée au système est décrite par un champ de vitesse d'amplitude infiniment petite,
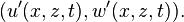
où les indices indiquent les dérivations partielles. En outre, dans un fluide incompressible initialement en mouvement stationnaire, il n'y a pas de tourbillon, et le champ de vitesse du fluide demeure irrotationnel, soit
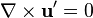
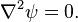
où

Le domaine sur lequel on résout le problème est le suivant : le fluide indexé « L » est confiné à la région
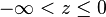
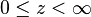
La première de ces conditions est fournie par les données aux limites. Les vitesses de perturbation
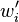
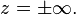
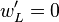
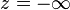
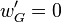
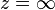
Les trois autres conditions sont fournies par le comportement de l’interface
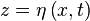
Continuité de la composante verticale de vitesse ; en z = η, les composantes verticales de vitesse doivent se raccorder :
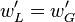
Par un développement limité en
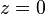
C’est l’équation exprimant la condition d’interface.
Condition de surface libre : Le long de la surface libre
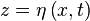
Par linéarisation, on obtient simplement
où la vitesse
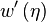
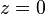
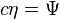
Saut de pression à l'interface: Dans le cas où l'on prend en compte une tension superficielle, le saut de pression à travers l’interface en z = η est donné par l’équation de Laplace :
où σ est la tension superficielle et κ est la courbure de l’interface, dont une approximation s'obtient en linéarisant :
Ainsi,
Toutefois, cette condition fait intervenir la pression totale (=pression de base+perturbation), c'est-à-dire
(Comme d'habitude, on peut linéariser les perturbations des différentes grandeurs le long de la surface z=0.) En exprimant l’équilibre hydrostatique, sous la forme
on obtient
L’altération du champ de pression est évaluée par les fonctions de courant, grâce à l’équation de l'impulsion horizontale tirée des équations d'Euler linéarisées pour les perturbations,
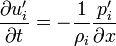
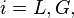
Reportant cette dernière équation avec la condition de saut,
En exploitant la deuxième condition d'interface
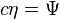
où il est d'ailleurs inutile d'indexer
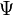
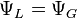
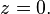
Solution
À présent qu'on a décrit mathématiquement le modèle d'écoulement stratifié, la solution est à portée. L’équation des lignes de courant
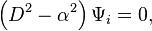
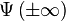
La première condition d’interface édicte que
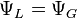
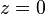
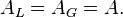
Reportant la solution dans cette équation, on forme la relation
Le A se simplifie de part et d'autre, et il reste
Pour interpréter complètement ce résultat, il est intéressant de considérer le cas où la tension superficielle est nulle. Dans ce cas,
et il est ainsi clair que
- si
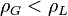
 et c est réel. C’est ce qui advient quand le fluide le plus léger est au-dessus;
et c est réel. C’est ce qui advient quand le fluide le plus léger est au-dessus; - si
 ,
,
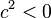
Donc, lorsque le fluide le plus lourd est au-dessus,
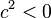
où
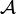
et qu'elle est associée à la position η de l’interface par :
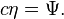
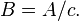
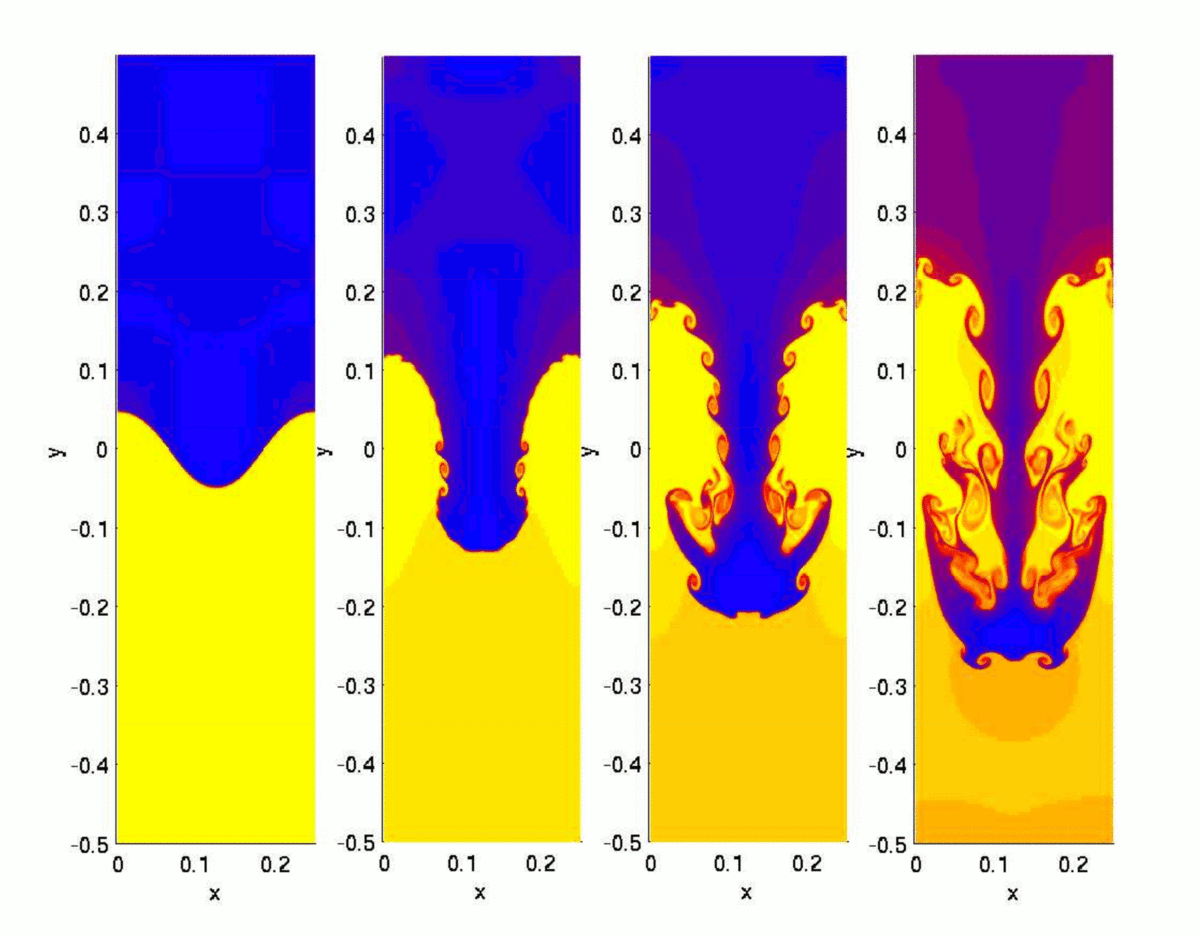
Le temps caractéristique de croissance de la surface libre
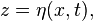
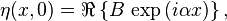
qui croît exponentiellement avec le temps. Ici B désigne l’amplitude de la perturbation initiale, et
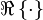
En général, la condition pour que l’instabilité soit linéaire est que la partie imaginaire de la célérité complexe c soit positive. Finalement, le rétablissement de la tension superficielle diminue c2 en module et a donc un effet stabilisant. En effet, il existe un domaine d'ondes courtes pour lesquelles la tension superficielle stabilise le système et empêche l’instabilité.
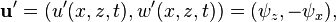
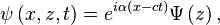
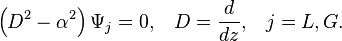

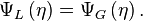
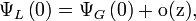
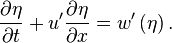
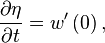
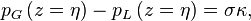
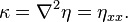
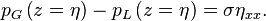
![\left[P_G\left(\eta\right)+p'_G\left(0\right)\right]-\left[P_L\left(\eta\right)+p'_L\left(0\right)\right]=\sigma\eta_{xx}.\,](https://static.techno-science.net/illustration/Definitions/autres/f/f80d4844b332a7028aecdc125f028475_295f216492d04ed8c726eb1a2ce488d4.png)

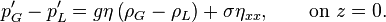
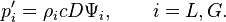
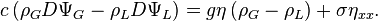
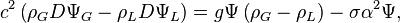

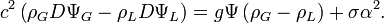
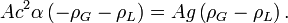
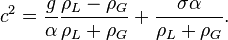
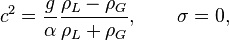
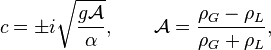
![\Psi\left(x,z,t\right)=Ae^{-\alpha|z|}\exp\left[i\alpha\left(x-ct\right)\right]=A\exp\left(\alpha\sqrt{\frac{g\tilde{\mathcal{A}}}{\alpha}}t\right)\exp\left(i\alpha x-\alpha|z|\right)\,](https://static.techno-science.net/illustration/Definitions/autres/f/fe041d7704ca1ccf22fb1d9d59858576_631d873135f3680c0e775899b305af7f.png)