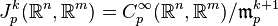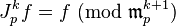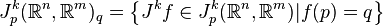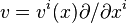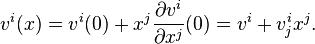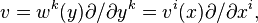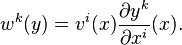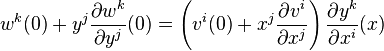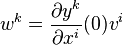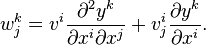Jeudi 1er Mai 2025
Rechercher 🔍

Jet (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Jets de fonctions entre espaces euclidiens - Jets de fonctions entre deux variétés - Définitions rigoureuses des jets en un point d’un espace euclidien - Jets de sections

Définitions rigoureuses des jets en un point d’un espace euclidien

Cette sous-section s’intéresse à deux définitions rigoureuses des jet d’une fonction en un point, suivies d’une discussion sur le théorème de Taylor. Ces définitions s’avèreront utiles plus tard, lors de la définition intrinsèque du jet d’une fonction définie ente deux variétés.

Définition analytique

La définition suivante utilise une approche analytique pour définir les jets et les espaces de jets. Elle peut être généralisée à des fonctions régulières entre espaces de Banach, à des fonctions analytiques entre des domaines réels ou complexe, à l’analyse p-adique, et à d’autre branches de l’analyse.

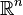
Soit l'espace vectoriel C^\infty({\mathbb R}^n,{\mathbb R}^m) des fonctions régulières f:{\mathbb R}^n\rightarrow {\mathbb R}^m , soit k un entier positif ou nul, et soit p un point de {\mathbb R}^n . On définit la relation d'équivalence E_p^k sur cet espace de la manière suivante : f et g sont équivalentes jusqu'à l'ordre k si et seulement f et g ont la même valeur en p ainsi que toutes leurs dérivées partielles jusqu'à l'ordre k inclus. En bref, f \sim g \,\! au sens de E_p^k si et seulement si f − g = 0 jusqu'à l'ordre k inclus.

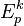
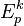
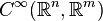
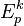
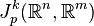
L'espaces des jets d'ordre k de C^\infty({\mathbb R}^n,{\mathbb R}^m) en p est par définition l'ensemble des classes d'équivalences de E^k_p , et noté par J^k_p({\mathbb R}^n,{\mathbb R}^m) .

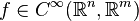
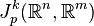
Le jet d'ordre k en p d'une fonction régulière f\in C^\infty({\mathbb R}^n,{\mathbb R}^m) est par définition la classe d'équivalence de f dans J^k_p({\mathbb R}^n,{\mathbb R}^m) .

Définition algébro-géométrique

La définition suivante utilise des notions de géométrie algébrique et algèbre commutative pour établir la notion de jet et d'espace de jets. Bien que cette définition ne soit pas particulièrement adaptée en elle-même à une utilisation en géométrie algébrique, puisqu'elle est forgée dans la catégorie régulière, elle peut facilement être adaptée à de tels usages.

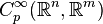
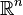
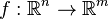
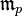
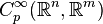
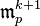
Soit C_p^\infty({\mathbb R}^n,{\mathbb R}^m) l'espace vectoriel des germes, en un point p de {\mathbb R}^n , de fonctions régulières f:{\mathbb R}^n\rightarrow {\mathbb R}^m . Soit {\mathfrak m}_p l'idéal des fonctions qui s'annulent en p. (C'est en fait l'idéal maximal pour l'anneau local C_p^\infty({\mathbb R}^n,{\mathbb R}^m) .) Alors l'ideal {\mathfrak m}_p^{k+1} est l'ensemble des germes de toutes les fonctions qui s'annulent en p jusqu'à l'ordre k inclus. On peut maintenant définir l'espaces des jets en p par :

J^k_p({\mathbb R}^n,{\mathbb R}^m)=C_p^\infty({\mathbb R}^n,{\mathbb R}^m)/{\mathfrak m}_p^{k+1}

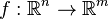
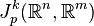
Si f:{\mathbb R}^n\rightarrow {\mathbb R}^m est une fonction régulière, on peut définir le jet d'ordre k de f en p comme l'élément de J^k_p({\mathbb R}^n,{\mathbb R}^m) donné par :

J^k_pf=f\ (\hbox{mod}\ {\mathfrak m}_p^{k+1})

Le théorème de Taylor

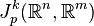
Indépendamment de la définition des jets, le théorème de Taylor (ou ses diverses généralisations : théorème de Laurent, théoreme de Fourier) établit un isomorphisme canonique d'espaces vectoriels entre J^k_p({\mathbb R}^n,{\mathbb R}^m) et {\mathbb R}^m[z]/(z^{k+1}) . Et donc dans le contexte euclidien, les jets sont typiquement identifiés, par cet isomorphisme, aux polynômes qui les représentent.

Espaces de jets d'un point à un point

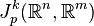
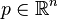
Nous avons définit l'espace J^k_p({\mathbb R}^n,{\mathbb R}^m) des jets en un point p\in {\mathbb R}^n . Le sous-espace des jets des fonctions f telles que f(p)=q est noté :

J^k_p({\mathbb R}^n,{\mathbb R}^m)_q=\left\{J^kf\in J^k_p({\mathbb R}^n,{\mathbb R}^m)|f(p)=q\right\}

Jets de sections

Cette sous-section traite de la notion des jets de section locales d'un fibré vectoriel. Presque chaque point de cette section peut être généralisé mutatis mutandis au cas d'une section locale d'un fibré, d'un fibré de Banach sur une variété de Banach, d'un fibré, ou d'un faisceau quasi-cohérent sur un schéma. De plus cette liste d'exemples de généralisations possibles n'est pas exhaustive.

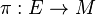
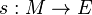
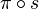
Soit E un fibré vectoriel régulier de dimension finie sur une variété M, ayant pour projection \pi:E\rightarrow M . Alors les sections de E sont des fonctions régulières s:M\rightarrow E telles que \pi\circ s est l'automorphisme identité de M. Le jet d'une section s au voisinage d'un point p est simplement le jet en p de cette fonction régulière de M dans E.

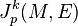
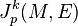
L'espace des jets de sections en p est noté J^k_p(M,E) . Bien que cette notation puisse prêter à confusion avec l'espace plus général des jets de fonctions entre deux variétés, typiquement, le contexte élimine de telles ambiguïtés. Contrairement aux jets de fonctions d'une variété dans une autre variété, l'espace des jets de sections en p hérite de la structure d'espace vectoriel des sections elles-mêmes. Quand p varie dans M, l'espac des jets J^k_p(M,E) forme un fibré vectoriel sur M, le fibré des jets d'ordre k de E, noté Jk(E).

  • Exemple: Le fibré des jets d'ordre 1 du fibré tangent.
On travaille en coordonnées locales en un point. Soir un champ de vecteurs
v=v^i(x)\partial/\partial x^i
dans un voisinage de p dans M. Le jet d'ordre 1 de v est obtenu en prenant le polynôme de Taylor d'ordre 1 des coefficients du champ de vecteurs:
v^i(x)=v^i(0)+x^j\frac{\partial v^i}{\partial x^j}(0)=v^i+v^i_jx^j.
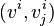
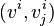
Dans le système de coordonnées en x, le jet d'ordre 1 en un point peut être identifié à une liste de nombres réels (v^i,v^i_j) . De la même manière, un vecteur tangent en un point peut être identifié avec la liste (vi), soumise à un loi de transformation pour un changement de système de coordonnées. Il reste à savoir comment cette liste (v^i,v^i_j) est affectée par un changement de système de coordonnées.
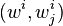
Considérons donc cette loi de transformation en passant à un autre système de coordonnées yi. Soient wk les coefficients du champ de vecteur v dans le système de coordonnées y. Alors dans ce système, le jet d'ordre 1 de v est une nouvelle liste de réels (w^i,w^i_j) . Puisque
v=w^k(y)\partial/\partial y^k=v^i(x)\partial/\partial x^i,
il s'en suit que
w^k(y)=v^i(x)\frac{\partial y^k}{\partial x^i}(x).
Ainsi
w^k(0)+y^j\frac{\partial w^k}{\partial y^j}(0)=\left(v^i(0)+x^j\frac{\partial v^i}{\partial x^j}\right)\frac{\partial y^k}{\partial x^i}(x)
En développant la série de Taylor, on a
w^k=\frac{\partial y^k}{\partial x^i}(0) v^i
w^k_j=v^i\frac{\partial^2 y^k}{\partial x^i\partial x^j}+v_j^i\frac{\partial y^k}{\partial x^i}.
On remarque que la loi de transformation est second ordre en les fonctions de transitions du système de coordonnées.
Jets de fonctions entre deux variétés
- Introduction - Jets de fonctions entre espaces euclidiens - Jets de fonctions entre deux variétés - Définitions rigoureuses des jets en un point d’un espace euclidien - Jets de sections
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.113 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise