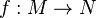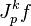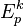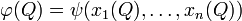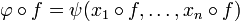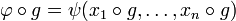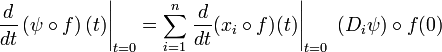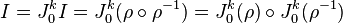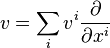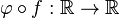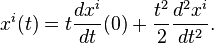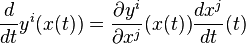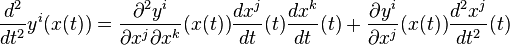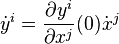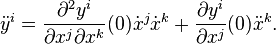Jet (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Jets de fonctions entre deux variétés
Si M et N sont deux variétés différentiables, comment peut-on définir le jet d'une fonction
Cette section commence en introduisant la notion de jets de fonctions de la ligne réelle vers une variété. Elle montre que de tels jets forment un fibré, analogue au fibré tangent, qui est un fibré associé d'un un groupe de jets. Elle poursuit en traitant la question de la définition le jet d'une fonction entre deux variétés régulières. Tout au long de cette section, on adopte une approche analytique des jets. Bien qu'une approche algébro-géométrique soit adaptée à de nombreuses autres applications, elle est trop subtile pour être adoptée systématiquement ici.
Jets de fonctions de la ligne réelle vers une variété
Soit M une variété régulière contenant le point p. Nous allons définir les jets de courbes passant par p, ce par quoi nous désignons des fonctions régulières
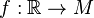
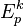
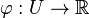
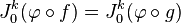
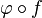
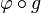
On pose maintenant, par définition, que le jet d'ordre k d'une courbe f en p est la classe d'équivalence de f pour la relation
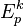
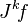
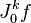
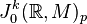
Quand p varie dans M,
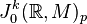
Pour montrer que TkM est un fibré, il est instructif d'examiner les propriétés de
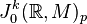
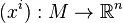
Proposition. Deux courbes f et g passant par p sont équivalentes modulo
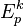
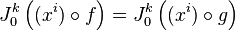
- En effet, dans cette proposition le côté seulement si est évident, puisque chacune des n fonctions x1,...,xn est une fonction régulière de M dans
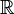
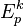
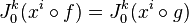
- Invresement, supposons que φ est une fonction régulière à valeur réelle définie sur M dans un voisinage de p. Puisque chaque fonction régulière a une expression en coordonnées locales, φ peut être exprimé comme une fonction de ces coordonnées. En particulier, si Q est un point de M près de p, alors
- pour une fonction ψ de n variables réelles à valeur réelle. Et donc, pour deux courbes f et g passant par p, on a
- Maintenant, la règle de dérivation des fonctions composées permet de démontrer le côté si de la proposition. Par exemple, si f et g sont des fonctions de la variable réelle t , alors
- qui est égal à la même expression évaluée en g au lieu de f, en se souvenant que f(0)=g(0)=p et que f ont un contact g d'ordre k dans le système de coordonnées (xi).
Ainsi l'espace TkM admets localement une structure de fibré trivial au voisinage de chaque point. Maintenant, afin de prouver que cet espace est en fait un fibré, il suffit de prouver qu'il a des fonctions de transition régulière pour un changement de variable. Soit
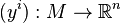
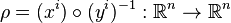
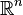
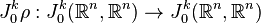
ce qui montre que
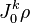
Intuitivement, ceci veut dire que le jet d'une courbe passant par p peut être exprimé par les termes de sa série de Taylor en coordonnées locale sur M.
Exemples en coordonnées locales:
- Ainsi qu'indiqué précédemment, le jet d'ordre 1 d'une courbe passant par p est un vecteur tangent. Un vecteur tangent en p est un opérateur différentiel du premier ordre agissant sur des fonctions à valeur réelles régulières en p. En coordonnées locales, chaque vecteur tangent a la forme
- Pour un tel vecteur tangent v, soit f la courbe donnée système de coordonnées xi par
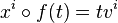
- est une fonction à valeur réelle d'une seule variable dont le jet d'ordre 1 est donné par
-
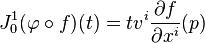
-
- ce qui prouve que l'on peut naturellement identifier les vecteurs tangent en un point avec les jets d'ordre 1 des courbes passant par ce point.
- L'espace des jets d'ordre 2 des courbes passant par un point.
- Dans un système de coordonnées locales noté xi centré en un point p, on peut exprimer le polynôme de Taylor du deuxième ordre d'une courbe f(t) par
- Ainsi dans le système de coordonnées x, le jet d'ordre 2 d'une courbe passant par p est identifié à une liste de nombres réels
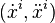
- Soit (yi) un autre système de coordonnées. En appliquant la règle de dérivation des fonctions composées,
-
- Et donc la loi de tranformation est obtenue en évaluant ces deux expressions en t=0.
-
- On remarque que la loi de transformation pour les jets d'ordre 2 est du deuxième ordre en les fonctions de transition du système de coordonnées.
Jets de fonctions d'une variété vers une variété
Nous sommes maintenant prêts à définir le jet d'une fonction d'une variété vers une varité.
Soient M et N deux variétés régulières. Soit p un point de M. On considère l'espace
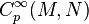
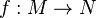
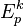
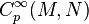
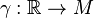
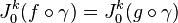
L'espace des jets
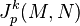
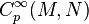
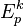
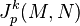
Si