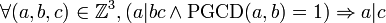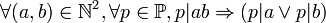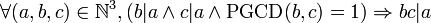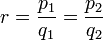Lemme d'Euclide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques le lemme d'Euclide est un résultat d'arithmétique élémentaire qui correspond à la Proposition 30 du Livre VII des Éléments d'Euclide. Il énonce que :
Théorème — Si un nombre premier p divise le produit de deux nombres entiers b et c, alors p divise b ou c.
Une généralisation est connue sous le nom de lemme de Gauss:
Théorème — Si un nombre entier a divise le produit de deux autres nombres entiers b et c, et que a et b sont premiers entre eux, alors a divise c.
Ceci peut être noté de façon formelle :
Dans le traité de Gauss, les Disquisitiones arithmeticae, l'énoncé du lemme d'Euclide constitue la proposition 14 (section 2) et est utilisée pour prouver la théorème de factorisation en nombres premiers. Le lemme de Gauss en découle (article 19).
Les noms de ces deux propositions sont parfois confondus. On notera d'ailleurs que le lemme de Gauss apparaît déjà dans les Nouveaux éléments de mathématiques de Jean Prestet au XVIIe siècle.
Le lemme d'Euclide se généralise aux polynômes (cf l'article Arithmétique des polynômes), ainsi qu'à tout anneau factoriel.
Démonstration
Soit
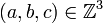
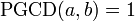
Comme a est premier avec b, d'après le théorème de Bachet-Bézout, il existe donc deux entiers relatifs u et v tels que :
- ua + vb = 1
Multiplions membre à membre par c :
- uac + vbc = c
Comme a | bc, il existe un entier relatif k tel que bc = ka, d'où :
- uac + vka = c
- (uc + vk)a = c
Cette relation montre que a | c.
Réciproque du lemme de Gauss
Si a,b sont deux entiers tels que, pour tout entier c, a divise bc implique que a divise c alors a et b sont premiers entre eux.
En effet, soit d un diviseur commun à a et b : on peut écrire a = a'd et b = b'd. Par hypothèse, comme a divise ba', on a que a divise a' donc d = 1, CQFD.
Conséquences
Première conséquence
Énoncé
Soient a et b deux entiers naturels non nuls et p un nombre premier. Si p divise le produit ab, alors p divise a ou p divise b. (Cet énoncé est en fait la forme originelle du Lemme d'Euclide.)
Démonstration
- Si p divise a, alors la propriété est établie.
- Si p ne divise pas a, alors p et a sont premiers entre eux, puisque les seuls diviseurs positifs de p sont 1 et p. Ainsi, p est premier avec a, or p divise ab, donc d'après le théorème de Gauss, p divise b.
Deuxième conséquence
Énoncé
Soient a, b et c des entiers naturels non nuls. Si b et c sont premiers entre eux et divisent a, alors bc divise a.
Démonstration
- b divise a donc il existe un entier naturel k tel que a = kb.
- c divise a donc c divise kb. Comme c est premier avec b, d'après le théorème de Gauss, c divise k.
Il existe donc un entier naturel m tel que : k = mc.
Ainsi, a = kb = mbc. Autrement dit, bc divise a.
Généralisation
Soient
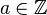
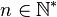
![(b_i)_{i\in[1,n]}\in{\mathbb{Z}^*}^n](https://static.techno-science.net/illustration/Definitions/autres/e/e222106fc8de4d0f7b1b53e947cd5c61_bf22b6e84e71dd2943a168e1e8b98d19.png)
![\forall (i,j)\in[1,n]^2, i\ne j \Rightarrow\operatorname{PGCD}(b_i,b_j)=1](https://static.techno-science.net/illustration/Definitions/autres/a/a627f17b4f9dc8a5e545e810bf5adec1_546f0ff4546e3ea45c52a37f1403ff64.png)
- On a alors :
![\left( \prod_{i=1}^n b_i \right)|a \Longleftrightarrow \forall i\in[1,n], b_i | a](https://static.techno-science.net/illustration/Definitions/autres/e/ee288e57c52ffcf6982e1c790af4f255_cbfa680b5598f54c6ad84c77b95a4fd7.png)
Troisième conséquence
Énoncé
Pour un rationnel r, il existe un unique couple d'entiers p et q premiers entre eux, q strictement positif, tels que r vaut p divisé par q.
Démonstration
Soit
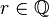
- Existence
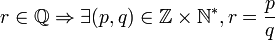
On note .
.
De même, .
Montrons que
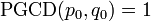
Selon le théorème de Bachet-Bézout,
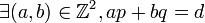
On a donc adp0 + bdq0 = d.
D'où ap0 + bq0 = 1.
Cette égalité assure que
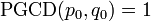
On a
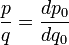
D'où
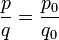
Le couple (p0,q0) convient donc bien.
- Unicité
Soit
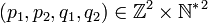
On a donc p1q2 = p2q1.
q2 | p1q2, donc q2 | p2q1.
Or
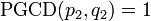
De même, q1 | p1q2. Or
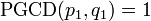
D'où q1 = q2, car
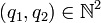
Puis p1 = p2.
La forme irréductible d'un rationnel est donc unique.