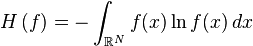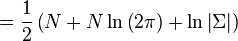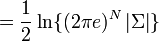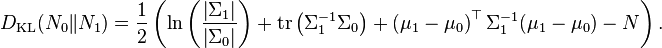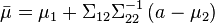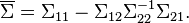Loi normale multidimensionnelle - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
- Les iso-contours d'une loi normale multidimensionnelle non singulière sont des ellipsoïdes centrés sur la moyenne μ. Les directions des axes principaux de ces ellipsoïdes sont les vecteurs propres de Σ. Les carrés des longueurs relatives de ces axes sont donnés par les valeurs propres associées à ces vecteurs propres.
- L'entropie différentielle de la loi normale multidimensionnelle est donnée par
- La divergence de Kullback-Leibler prend une forme particulière dans le cas de deux lois normales multidimensionnelles
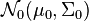
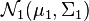
Distributions conditionnelles
Si μ et Σ sont partitionnées comme décrit ci-dessous
-
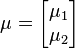
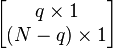
-
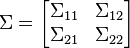
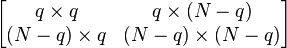
alors la distribution de x1 conditionnellement à x2 = a est une loi normale multidimensionnelle
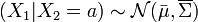
et la matrice de variance-covariance s'écrit
Cette matrice est le complément de Schur de
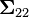
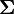
On remarquera que savoir que x2 vaut a change la variance mais que, de manière plus surprenante, la moyenne est aussi modifiée et ce par un décalage de
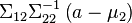
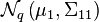
La matrice
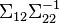
Applications
La loi normale multidimensionnelle est notamment utilisée dans le traitement d'images médicales. Ainsi elle est par exemple fréquemment utilisée dans l'imagerie du tenseur de diffusion. Cette imagerie modélise en effet la distribution des principales directions de diffusion de l'eau par une loi normale multidimensionnelle de moyenne nulle. Ainsi le tenseur en chaque point de l'image n'est autre que la matrice de covariance de la loi normale multidimensionnelle.
Une seconde application de la loi normale multidimensionnelle est la détermination, à partir des intensités dans des IRM du cerveau d'un patient, des différentes classes de tissus ( matière grise, matière blanche, liquide céphalo-rachidien) qui le composent. Cette technique est basée sur l'utilisation d'un algorithme espérance-maximisation dans lequel chacune des classes est modélisée par une loi normale multidimensionnelle dont la dimension est égale aux nombre de modalités utilisées pour la classification.