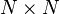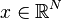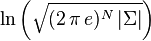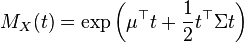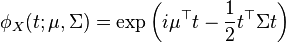Loi normale multidimensionnelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Distribution normale multidimensionnelle | |
|---|---|
| Paramètres |
Σ matrice de variance-covariance (matrice définie positive réelle |
| Support |
|
| Densité de probabilité (fonction de masse) |
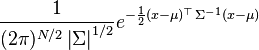
|
| Espérance | μ |
| Médiane (centre) | μ |
| Mode | μ |
| Variance | Σ |
| Asymétrie (statistique) | 0 |
| Entropie |
|
| Fonction génératrice des moments |
|
| Fonction caractéristique |
|
| modifier | |
On appelle loi normale multidimensionnelle, ou loi multinormale ou loi de Gauss à plusieurs variables, une loi de probabilité qui est la généralisation multidimensionnelle de la loi normale.
Alors que la loi normale classique est paramétrée par un scalaire μ correspondant à sa moyenne et un second scalaire σ2 correspondant à sa variance, la loi multinormale est paramétrée par un vecteur
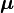
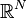
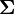
Dans le cas non dégénéré où Σ est définie positive, donc inversible, la loi normale multidimensionnelle admet une densité de probabilité
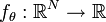
pour un vecteur
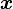
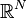
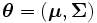
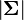
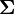
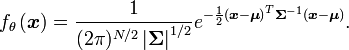
Cette loi est habituellement notée
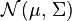
Loi non dégénérée
Cette section s'intéresse à la construction de la loi normale multidimensionnelle dans le cas non dégénéré où la matrice de variance-covariance Σ est définie positive.
Rappel sur la loi normale unidimensionnelle
Le théorème de la limite centrale fait apparaître une variable
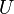
![E[U] = 0 \qquad E[U^2] = 1](https://static.techno-science.net/illustration/Definitions/autres/0/0ce2d3bc7cd55f58182415105479f9fa_5effb8f1f3266e99f1516a67535e9d4c.png)
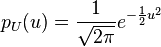
On passe à la variable de Gauss générale par le changement de variable
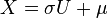
qui conduit à
![E[X] = \mu \qquad E[(X-\mu)^2] = \sigma^2](https://static.techno-science.net/illustration/Definitions/autres/8/81a423246fda5e1ad0bafc217b5ed044_b90731f9c9c58b74e66c0fe16826105d.png)
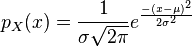
Cette loi est caractérisée par une exponentielle comportant un exposant du second degré.
Loi unitaire à plusieurs variables
Étant données N variables aléatoires indépendantes de même loi de Gauss centrée réduite, leur densité de probabilité jointe s'écrit :
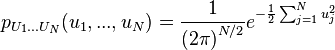
C'est la loi qui est à la base de la loi du χ².
Elle peut être synthétisée dans des formules matricielles. On définit d'abord le vecteur aléatoire
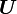
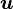
On peut associer au vecteur d'état le vecteur moyenne qui a pour composantes les moyennes des composantes, c'est-à-dire, dans ce cas, le vecteur nul :
![E[\boldsymbol{U}] = \boldsymbol{0}\,](https://static.techno-science.net/illustration/Definitions/autres/5/54ec09e55712226098dbb741ef27a418_b708a05c0224aab4f81ea311fbcffd85.png)
La matrice de covariance possède des éléments diagonaux (les variances) qui sont égaux à 1 tandis que les éléments non diagonaux (les covariances au sens strict) sont nuls : c'est la matrice unité. Elle peut s'écrire en utilisant la transposition :
![E[\boldsymbol{U} \boldsymbol{U}^T] = \boldsymbol{I}\,](https://static.techno-science.net/illustration/Definitions/autres/9/9fa073e1d1a6700e6e064b8beaef5537_abba1e22452241d60251d3637cde981b.png)
Enfin, la densité de probabilité s'écrit :
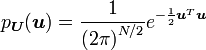
Loi générale à plusieurs variables
Elle s'obtient à partir d'un changement de variable linéaire
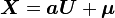
Le problème sera limité au cas d'une matrice
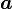
![E[\boldsymbol{X}] = \boldsymbol{a} E[\boldsymbol{U}] + \boldsymbol{\mu} = \boldsymbol{\mu}\,](https://static.techno-science.net/illustration/Definitions/autres/8/8e1d805fae327ac1bd5245b1f612a699_007f2f8fe8020c81de916140b42ca349.png)
et la matrice de covariance
![E[\boldsymbol{(X-\mu)} \boldsymbol{(X-\mu)}^T] = E[\boldsymbol{a} \boldsymbol{U} \boldsymbol{U}^T \boldsymbol{a}^T] = \boldsymbol{a}\boldsymbol{a}^T= \boldsymbol{\Sigma}\,](https://static.techno-science.net/illustration/Definitions/autres/c/c7280b8b1d72036530ded212d1def124_c792ea50e6b6105d9bcc476b694023fe.png)
La densité de probabilité s'écrit
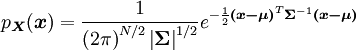
Remarques diverses
- Un nouveau changement de variables linéaire appliqué à
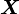
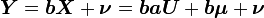
- Les formules essentielles, obtenues commodément à partir du calcul matriciel, se traduisent en termes scalaires :
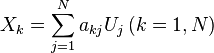
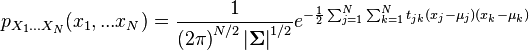
les
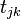
- L'exposant dans la formule qui précède est du second degré par rapport à toutes les variables. On vérifie qu'une intégration par rapport à l'une d'entre elles donne un résultat analogue. (N-1) intégrations successives aboutissent à une loi de probabilité marginale munie d'un exposant quadratique : chaque variable est gaussienne, ce qui n'était pas évident a priori.
- En combinant les remarques précédentes, on aboutit au résultat selon lequel toute combinaison linéaire des composantes d'un vecteur gaussien est une variable gaussienne.
- Dans cette loi de probabilité jointe, à tout couple de variables décorrélées correspond une matrice de covariance diagonale, ce qui assure leur indépendance. En effet, le couple est lui-même gaussien, et sa densité jointe est le produit des densités de ses deux composantes.
- Le terme présent dans l'exponentielle
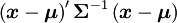
![\mu = [\mu_1, \dots, \mu_N]^\top](https://static.techno-science.net/illustration/Definitions/autres/c/c4117161cbd483a9f60c55f017c34205_05e5523c3e3ae42ac1fd25fe5b9afc59.png)