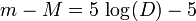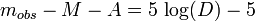Magnitude absolue - Définition
La liste des auteurs de cet article est disponible ici.
Magnitude apparente et distance
La comparaison de la magnitude absolue avec la magnitude apparente (qui est la magnitude observée effectivement sur Terre) permet une estimation de la distance de l'objet. Suivant la décroissance de la luminosité avec le carré de la distance, on obtient:
où m est la magnitude réelle apparente, M la magnitude absolue et D la distance exprimée en parsecs. La valeur μ = m − M est aussi appelée module de distance, ce dernier étant plus souvent utilisé pour les objets extra-galactiques.
Pour avoir la magnitude absolue, il faut des modèles stellaires, et connaître la température de l'étoile (qui peut s'obtenir à partir de l'indice de couleur, qui n'est autre que la différence des magnitudes apparentes d'un objet dans deux bandes spectrales différentes).
Dans la pratique, la seule quantité aisément accessible est évidemment la magnitude observée, qui est en fait la combinaison de la magnitude apparente et de l'absorption interstellaire: m = mr = mobs − A, où A est l'absorption.
La connaissance de l'absorption est souvent critique. L'absorption modifie la luminosité réelle de l'objet, à cause de la diffusion de la lumière par les grains de poussière interstellaire. La distribution chaotique des grains dans l'espace rend extrêmement difficile l'estimation de l'absorption interstellaire, puisque celle qui est valable dans une direction donnée pour un objet donné, peut être significativement différente pour l'étoile d'à côté (en faisant l'hypothèse que les deux étoiles sont à la même distance). De plus, à cause de l'effet de diffusion, l'absorption dépend de la longueur d'onde, et est donc un effet chromatique (voir article détaillé).
Donc, en pratique, l'équation s'écrit comme suit:
et seule la valeur de mobs est facile à mesurer.
Objets célestes très lumineux
Quelques étoiles visibles à l'œil nu ont une magnitude absolue qui fait qu'elles seraient plus brillantes que les planètes si elles étaient effectivement éloignées de seulement 10 parsecs. C'est le cas des supergéantes Rigel (-7,0), Deneb (-7,2), Naos (-7,3) et Bételgeuse (-5,6). À titre de comparaison, l'objet le plus brillant du ciel après le Soleil (qui a une magnitude apparente de -26.73) et la pleine lune (-12) est Vénus avec une magnitude apparente de -4,3.
Le dernier objet céleste dont la magnitude apparente fut comparable à la magnitude absolue des trois objets ci-dessus était une supernova qui se produisit en 1054 (et nommée SN 1054) et dont aujourd'hui il ne subsiste qu'une nébuleuse planétaire, la nébuleuse du Crabe, et un pulsar. Les astronomes de l'époque rapportèrent que la luminosité de cet objet était si grande qu'ils pouvaient lire en pleine nuit, voir les ombres portées de sa lumière et l'observer en plein jour.