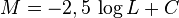Magnitude absolue - Définition

Introduction

En astronomie, la magnitude absolue indique la luminosité intrinsèque d'un objet céleste, au contraire de la magnitude apparente qui dépend de la distance à l'astre et de l'extinction dans la ligne de visée. Pour un objet situé à l'extérieur du système solaire, elle est définie par la magnitude apparente qu'aurait cet astre s'il était placé à une distance de référence fixée à 10 parsecs (environ 32,6 années-lumière) en l'absence d'extinction interstellaire. Pour un corps du système solaire, il s'agit de la magnitude apparente qu'il aurait à une unité astronomique à la fois de la Terre et du Soleil, en supposant sa face visible totalement illuminée. Pour les météores (étoiles filantes), il s'agit de leur magnitude apparente s'ils étaient observés à 100 km d'altitude au zénith.

Comme toutes les magnitudes, elle est une fonction affine décroissante du logarithme de la luminosité de l'objet : la magnitude augmente d'une unité lorsque la luminosité est divisée par 2,5 (environ). La différence entre magnitude apparente et relative, dans le cas d'un objet situé en-dehors du système solaire, est donnée par le module de distance. La magnitude absolue peut être donnée dans une bande spectrale, le plus souvent le filtre V du système photométrique de Johnson, ou comme magnitude bolométrique, à savoir qu'elle décrit le flux reçu dans toutes les longueurs d'onde. La différence entre la magnitude absolue en bande V et cette dernière constitue la correction bolométrique.

Définition

Par définition de l'Union astronomique internationale, « la magnitude absolue d'un objet est la magnitude que verrait un observateur situé à une distance d'exactement 10 parsecs [Note : 32,6 années-lumière] de cet objet ».

La magnitude absolue est ainsi une échelle logarithmique directement liée à la luminosité de l'étoile. La définition de la magnitude absolue s'écrit en termes mathématiques :

où L est la luminosité de l'étoile exprimée en unités de luminosité solaire et C une constante. S'agissant d'une échelle logarithmique inversée, plus un astre est lumineux, plus sa magnitude est faible.

Selon que la luminosité est calculée sur une bande spectrale bleue B (autour de 436 nm) ou visible V (aux alentours de 545 nm), la magnitude absolue est notée M_B ou M_V. La constante est choisie aujourd'hui telle que les magnitudes absolues du Soleil dans les bandes B et V soient M_B = 5,48 et M_V = 4,83.

Quand on considère la totalité du spectre électromagnétique, des ondes radio aux rayons gamma, et pas seulement une bande spectrale donnée, on parle de luminosité bolométrique, et donc de magnitude bolométrique.

Les magnitudes absolues des étoiles s'étendent généralement de -10 à +17 en fonction de leur type spectral : une supergéante bleue a une magnitude absolue descendant jusqu'à -10 tandis que celle d'une naine rouge peut aller jusqu'à +17. Le Soleil, avec une magnitude absolue de +4,8 se situe à peu près à mi-chemin de ces deux extrêmes.

Magnitude absolue des objets du Système solaire

Dans ce cas particulier, la distance de référence n'est pas 10 parsec, mais une unité astronomique.

Les objets du système solaire comme les planètes, les comètes ou les astéroïdes ne font que réfléchir la lumière qu'ils reçoivent du soleil et leur magnitude apparente dépend donc, non seulement de leur distance à la Terre, mais aussi de leur distance au Soleil. La magnitude absolue de ces objets est donc définie comme leur magnitude apparente s'ils étaient situés à une unité astronomique du soleil et une unité astronomique de la terre, tout en étant avec un angle de phase de zéro degré (« pleine lune », toute la surface visible depuis la terre est éclairée).

Pour un corps situé à une distance r de la Terre et a du soleil, la relation entre sa magnitude (relative) m et sa magnitude absolue, notée H, est donnée par la formule :

où p(χ) est l'intégrale de phase, fonction de χ, représentant l'angle de phase de l'objet ; r et a doivent être exprimées en unités astronomiques.

L'intégrale de phase p(χ) peut-être approximée par la formule :

La situation décrite par la définition de la magnitude absolue est physiquement impossible : l'angle de phase est de 30 degrés pour un astre sphérique à une unité astronomique de la Terre et du soleil. Elle doit être considérée comme une référence — et elle se trouve donner le bon ordre de grandeur pour le résultat observé.