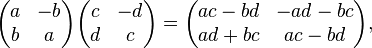Nombre complexe - Définition

Structure du corps des complexes

Les racines carrées d'un nombre complexe s'écrivent facilement lorsque celui-ci est sous forme trigonométrique : celles de z = re^iθ sont et et sont opposées l'une de l'autre.
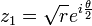
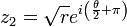
L'existence de deux racines carrées, dans le corps des nombres complexes, pour tout nombre complexe non nul (y compris pour tout réel strictement négatif) est une propriété qui n'est pas vérifiée par restriction au corps des réels, puisqu'aucun réel strictement négatif ne peut s'obtenir comme le carré d'un nombre réel.

Plus généralement, tout polynôme à coefficients complexes (donc, en particulier, tout polynôme à coefficients entiers ou rationnels), non constant, admet au moins une racine (ce qui implique qu’il en admet autant que son degré, en les comptant avec leurs multiplicités). On dit que le corps des complexes est algébriquement clos. Ce résultat est connu en France sous le nom de Théorème de d'Alembert-Gauss, dans d'autres pays sous le nom de théorème fondamental de l'algèbre.

En fait, le corps des complexes est la clôture algébrique du corps des réels, c'est-à-dire le plus petit corps qui contienne le corps des réels et qui soit algébriquement clos. Du point de vue de la théorie de Galois, on peut considérer les automorphismes du corps des complexes : l'identité et la conjugaison sont ses seuls automorphismes continus (on peut remplacer l'hypothèse « continu » par, au choix, « mesurable » ou « tel que l'image de tout réel est un réel »). En supposant l'axiome du choix on peut construire des automorphismes « exotiques » de ce corps: voir automorphismes de corps non continus de C.

Construction

Il existe plusieurs manières courantes de construire le corps des nombres complexes à partir de l'ensemble des nombres réels et de ses opérations arithmétiques élémentaires. Outre que les objets ainsi définis sont tous isomorphes, les constructions présentées ci-après mettent en lumière trois caractéristiques importantes :

1. Le corps des réels est clairement identifié comme un sous-ensemble du corps des complexes et les opérations d'addition et de multiplication sont préservées dans la nouvelle structure. Le nombre réel 1 reste neutre pour la multiplication.
2. Il existe un nombre complexe canoniquement choisi dont le carré vaut − 1, bien que son opposé vérifie aussi cette propriété.
3. Deux paramètres réels sont nécessaires et suffisants pour décrire tous les nombres complexes, ce qui souligne la structure d'espace vectoriel réel de dimension 2 avec une base canonique.

Vecteur du plan euclidien

On peut définir un nombre complexe comme un vecteur du plan muni de sa base canonique.

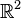
Chaque nombre complexe est donc représenté par un couple (a,b) de nombre réels.
L'addition correspond à celle des vecteurs, c'est-à-dire l'addition des coordonnées terme à terme :

.

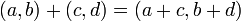
La multiplication est définie « arbitrairement » par :

.

L'ensemble des réels s'identifie avec la droite et l'élément est le deuxième vecteur de base (0,1). Le module d'un nombre complexe correspond enfin à la norme euclidienne du vecteur associé et l'argument est une mesure de l'angle formé par le vecteur associé avec le premier vecteur de base.

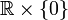
Cette définition présente l'avantage de la simplicité, puisqu'elle exige peu de prérequis mathématiques. Elle est en outre adaptée à la des nombres complexes.

Matrice de similitude

Il est intéressant de définir un nombre complexe comme une matrice de similitude directe à coefficients réels, car les opérations matricielles induisent précisément la structure algébrique voulue. En outre, le module et l'argument deviennent respectivement le rapport et une mesure de l'angle de la similitude.
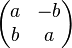
Il faut cependant vérifier que l'ensemble de ces matrices est stable par produit :

ce qui justifie au passage la commutativité du produit et assure l'isomorphisme entre cette structure et .
L'ensemble des réels s'identifie alors à l'ensemble des matrices diagonales de la forme , l'unité étant représentée par la matrice identité. L'élément désigne classiquement la matrice .
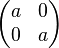
Le déterminant correspond au carré du module, ce qui entraîne que toutes les éléments non nuls sont inversibles et la méthode des cofacteurs démontre la stabilité par inverse.

Ce point de vue fournit une construction naturelle qui peut être adaptée pour obtenir l'algèbre réelle des quaternions. Il donne en outre une interprétation géométrique de la multiplication des nombres complexes comme composition de similitudes du plan. La conjugaison est enfin représentée par la transposition de matrices.

Classe d'équivalence de polynômes

Un nombre complexe peut enfin être vu comme un polynôme réel d'indéterminée i, où le carré i² est identifié avec le polynôme constant de valeur − 1, donc avec les identifications i³ = − i ; i⁴ = 1…
Formellement, cela revient à assimiler l'ensemble des nombres complexes à l'espace quotient , dans lequel deux polynômes appartiennent à la même classe d'équivalence si et seulement s'ils ont le même reste de division euclidienne par X² + 1.
Le caractère irréductible du polynôme X² + 1 assure directement la structure de corps. Les réels sont représentés par les polynômes constants et le degré 2 du polynôme diviseur est la dimension de l'ensemble comme espace vectoriel réel.

Cette conception très sophistiquée en apparence est peut-être celle qui décrit le mieux l'invention des nombres complexes, loin de la géométrie, à partir d'un seul générateur algébrique et d'une seule relation. Le formalisme (plus récent) du quotient d'un anneau euclidien (ici l'anneau des polynômes réels à une indéterminée) par un de ses idéaux irréductibles est à la base de la construction des extensions algébriques de corps.