Oscillateur paramétrique optique - Définition
La liste des auteurs de cet article est disponible ici.
Accordabilité d'un OPO
Dans un OPO utilisant l'accord de phase par biréfringence, les fréquences des ondes signal et complémentaire peuvent être changées continument par une simple rotation du cristal non-linéaire. En effet, en changeant l'angle θ entre la pompe et le cristal, la condition d'accord de phase sera vérifiée pour des fréquences signal et complémentaire différentes. Comme la conservation de l'énergie reste vérifiée, une augmentation de la fréquence du signal s'accompagnera d'une diminution de la fréquence complémentaire, et vice-versa.
Plus généralement, toute méthode permettant de faire varier sensiblement l'indice extraordinaire par rapport à l'indice ordinaire permet de changer l'accord de phase et donc d'accorder l'OPO. Ainsi, l'accord de phase en température se fait en chauffant un cristal biréfringent.
- tolérance : choix des lambda, accord de phase
- cône de fluorescence paramétrique + photo
- limitations: zone d'accord de phase, deff, transmission
- pas de résonance excitée : accordabilité
- quid de l'accord de phase en température ?
Phénomènes limitant l'efficacité d'un OPO
Désaccord de phase
Que se passe-t-il si l'accord de phase n'est pas réalisé, ou s'il est imparfait ? On parle alors de désaccord de phase non nul, et on note dans le cas colinéaire :
Dans ce cas, l'énergie transférée de la pompe au signal et au complémentaire finit par être rendue à la pompe, et ce de manière périodique au cours de la propagation dans le milieu. L'alternance de ces interférences constructives et destructives forme des zones « sombres » et « claires » (du point de vue de l'intensité d'une des trois ondes) qu'on appelle franges de Maker. Pour des puissances de pompe relativement faibles (en dessous de la saturation), l'intensité générée est donnée par :
où g est le gain paramétrique, proportionnel à la non-linéarité du milieu et à l'amplitude de l'onde de pompe, et
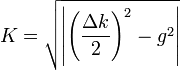
Pour un fort désaccord de phase, la demi période de ces franges est appelée longueur de cohérence et vaut
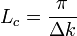
À l'accord de phase parfait en revanche (Δk = 0), la puissance est transférée de façon durable au signal et au complémentaire (en dessous de la saturation), selon la relation :
où l'approximation est valable pour un faible gain. Si on s'intéresse à l'intensité en sortie du milieu non-linéaire de longueur L en fonction du désaccord de phase, en se restreignant aux faibles gains, on obtient :
Ce que montre cette formule et la figure ci-contre, c'est que l'intensité générée peut rester importante même avec un faible Δk L : l'accord de phase n'est pas une condition stricte. Autrement dit, le processus de conversion de la pompe vers le signal et le complémentaire restera efficace :
- pour des fréquences de l'onde signal et complémentaire légèrement différentes, à fréquence de pompe fixe : c'est la tolérance en longueur d'onde, ou acceptance spectrale de l'OPO. On parle également de bande passante. Celle-ci est limitée par les différences entre les vitesses de groupe des différentes ondes. Elle est d'autant plus petite que le cristal est long. Sa valeur est très variable et peut atteindre es valeurs aussi importantes que 3 000 Ghz (soit plus de 10 nm à 1 μm) ;
- pour des angles de propagation des ondes différents : c'est l'acceptance angulaire de l'OPO. Elle peut être limitante dans le cas de faisceaux fortement focalisés.
Pour la conception d'un OPO, ces tolérances peuvent être des avantages ou des inconvénients, selon ce qu'on souhaite.
Walk-off
L'inconvénient majeur de l'accord de phase par biréfringence est justement... la biréfringence ! En effet, des ondes polarisées différemment vont se propager suivant des directions différentes dans le cristal, en suivant les rayons ordinaire O et extraordinaire E correspondant aux polarisations du même nom. Le décalage des faisceaux diminue leur recouvrement et donc la longueur d'interaction : l'efficacité diminue. Ce phénomène est communément désigné par le terme anglo-saxon de walk-off (littéralement : « marche en dehors »).
Dans certaines situations, il est possible de s'affranchir de cet effet tout en conservant un accord de phase. Dans ce cas les indices vus par les ondes dépendent peu de l'angle de propagation, ce qui rend l'accord de phase très tolérant : on parle alors d'accord de phase non critique.
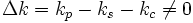
![I_{s,c}\left(z\right)=I_{s,c}\left(0\right)\left[1+\frac{g^2}{K^2}\sin^2\left(K z\right)\right]\,](https://static.techno-science.net/illustration/Definitions/autres/5/5e52bc4124b8a2d8915783f203d9f197_da8cc459ed8b646fc732641983c6bd7d.png)
![I_{s,c}\left(z\right)=I_{s,c}\left(0\right)\cosh^2\left(g z\right)\approx I_{s,c}\left(0\right)\left[1+\frac{1}{2}\left(g z\right)^2\right]\,](https://static.techno-science.net/illustration/Definitions/autres/6/604dc4516dc4eae3e068d364e8e2776b_0fd5c1186e558b2884c2b79782f99138.png)
![I_{s,c}\left( \frac{\Delta k L}{2}\right)=I_{s,c}\left(0\right)\left[1+\left(g L\right)^2 \operatorname{sinc}^2\left(\frac{\Delta k L}{2}\right)\right]\,](https://static.techno-science.net/illustration/Definitions/autres/8/8d6621fe02640fa6fed926ad7c6ac8ef_3ae1ffc360ae86b8f9951ccd9de182c0.png)

















































