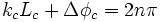Oscillateur paramétrique optique - Définition

Objet quantique ou classique ?

Dans le régime des variables continues (i.e. dans lequel on ne peut plus distinguer individuellement les photons), l'OPO est utilisé pour générer des états non classiques de la lumière. En effet, lorsque l'OPO est pompé sous son seuil d'oscillation, ce dernier présente des propriétés quantiques très intéressantes. On parle d'amplification paramétrique optique non dégénérée dont l'hamiltonien modèle est :

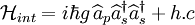
où désigne l'opérateur d'annihilation d'un photon de pompe (p), signal (s) et complémentaire (c), et g est une constante de couplage que l'on peut obtenir par une correspondance semi-classique notamment. L'interprétation corpusculaire de la conversion paramétrique est transparente sur cet hamiltonien.

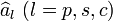
Si l'on se place à la dégénérescence de fréquence et de polarisation, et si la pompe est suffisamment intense, l'hamiltonien devient :

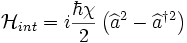
où χ désigne une nouvelle constante qui dépend de l'amplitude complexe de la pompe et de la non linéarité du cristal.

Si l'on écrit maintenant l'équation d'évolution des opérateurs d'annihilation, dans la représentation d'interaction, on est conduit à :

d'où :

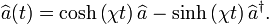
On rappelle l'expression des opérateurs de quadratures : La relation d'entrée-sortie de ces opérateurs après un temps d'interaction t_int = nL / c dans un cristal non linéaire de longueur L et d'indice n s'écrit :

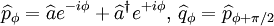
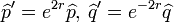
avec r = χt_int. On constate donc bien que la quadrature est comprimé d'un facteur s = e ^{− 2r} alors que la quadrature conjuguée est dilatée d'un facteur 1 / s. La relation d'incertitude qui conditionne les variances de ces quadratures est toujours vérifiée. L'opérateur d'évolution associé à cet hamiltonien d'interaction s'écrit alors de manière générale :

que l'on appelle un squeezer.

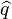
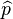
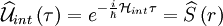
Lorsque l'on travaille sous le seuil d'oscillation de l'OPO (i.e. ses pertes ne sont alors plus compensées par l'injection de la pompe), les champs lumineux ont une valeurs moyennes nulles. Le squeezer agit donc sur un état de vide de photons . On obtient alors à la sortie de l'OPO des faisceaux toujours vides de photons mais dont les fluctuations sont cette fois comprimées en dessous de la limite quantique standard définies par les fluctuations du vide. Si l'on écrit maintenant cet opérateur complètement en termes des opérateurs et , on obtient :

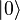
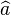
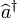
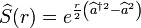
On constate alors facilement que l'action de cet opérateur sur le vide de photon conduit à un état ne peuplant que les états nombres pairs de photons.

Bistabilité et chaos

Tout comme certaines cavités Fabry-Perot comprenant un milieu non-linéaire, un OPO peut présenter de la bistabilité. Autrement dit, la puissance de sortie à une des longueurs d'onde peut prendre deux valeurs différentes pour une seule valeur de la puissance en entrée. Le passage d'un état à un autre se faisant par un basculement très rapide.

Dans certaines conditions (dépendant des pertes optiques et des longueurs de cavité), la puissance en sortie de l'OPO devient chaotique en fonction de la puissance en entrée. Il est alors possible d'observer les phénomènes de bifurcation par doublement de période et d'attracteur prévus par la théorie du chaos.

Ces phénomènes s'observent préférentiellement dans les OPO triplement résonnants.

Analogies et différences entre oscillateur paramétrique optique et laser

Les OPO et les lasers ont un certain nombre de points communs :

• ils nécessitent un milieu amplificateur et une cavité optique ;
• ils produisent un rayonnement cohérent et monochromatique de longueur d'onde optique ;
• ils peuvent être pompés par une autre source optique cohérente ;
• leur conception nécessite des connaissances et des technologies proches ou identiques.

En revanche, il existe un certain nombre de différences aussi bien théoriques que pratiques entre ces deux dispositifs, que nous nous proposons de détailler ici.

Trois ondes pour une, deux ou trois résonances

Dans un laser, l'onde générée est également l'onde oscillante. Dans un OPO en revanche, il y a trois ondes optiques couplées entre elles : pompe, signal et complémentaire. On peut alors envisager de nombreux schémas d'OPO selon la façon dont ces ondes sont mises en cavité :

• OPO simplement résonant (SROPO). Le signal est par exemple l'onde oscillante dans la cavité, tandis que le complémentaire générée dans le cristal est libre. On peut alors choisir de n'extraire que le complémentaire, ou bien d'extraire également le signal en employant un miroir de sortie partiellement réfléchissant.
• OPO doublement résonant (DROPO). Signal et complémentaire résonnent tous les deux dans la cavité. Le seuil d'oscillation est plus faible qu'en simplement résonant, ce qui le rend intéressant pour la réalisations d'OPO continus où l'intensité de l'onde pompe est relativement faible. En revanche, il faut que les résonances du signal et du complémentaire coïncident, ce qui n'est généralement pas le cas à cause de la dispersion. De plus, même en cas de coïncidence, la moindre fluctuation de la longueur optique de cavité risque de faire sortir le DROPO de la double résonance. Ce type d'OPO souffre donc d'instabilités de fréquence et d'intensité, particulièrement gênantes en régime continu ou lorsqu'on veut accorder l'OPO en fréquence. Une stabilisation active de la cavité par une électronique d'asservissement peut permettre de maintenir la double résonance. Il existe également des DROPO dans lesquels signal et complémentaires oscillent dans des cavités de longueurs différentes (DROPO à cavités imbriquées), ce qui permet de choisir et contrôler la coïncidence des résonances. Dans tous les cas une conception monolithique et robuste permet d'améliorer les choses.
• PR-DROPO. Un DROPO où l'un des deux ondes résonantes est la pompe.
• OPO triplement résonant (TROPO). Il s'agit d'un DROPO dans lequel la pompe oscille également. Cet OPO souffre des mêmes problèmes que le DROPO, en pire.
• OPO à retour de pompe (PE-OPO). Il s'agit d'un OPO pour lequel la pompe restante après un aller est renvoyée vers l'OPO afin de réaliser un double pompage.
• OPO à amplification intracavité (OPO-OPA). Il s'agit d'un OPO simplement résonant à deux cristaux non-linéaires. L'onde résonante, après passage dans le deuxième cristal, sert de pompe dans le deuxième cristal pour amplifier l'onde non résonante.
• OPO à résonances croisées (CROPO). Il s'agit d'un SROPO à deux cristaux pour lequel le signal est évacué de la cavité après le premier cristal et le complémentaire après le deuxième. La pompe et le signal se mélangent dans le premier cristal pour créer l'onde complémentaire, tandis que ce sont la pompe et le complémentaire qui se mélangent dans le deuxième cristal pour refaire du signal. On peut montrer que cet OPO est réellement simplement résonant car les ondes gardent une relation de phase entre elles qui maintient l'oscillation.

En fait, les variantes sont presque infinies. Il existe par exemple des OPO pour lesquels la pompe à ω_p n'est pas issue directement d'un laser externe, mais générée à l'intérieur de la cavité optique par doublage de fréquence dans un cristal non-linéaire pompé à ω_p/2 !

Effets thermiques

Une autre différence fondamentale entre un laser et un OPO est le mode de génération de la lumière. L'effet laser nécessite l'absorption de l'énergie de pompe avant restitution à l'onde générée, ce qui entraîne notamment une élévation de température du milieu laser. L'effet paramétrique, comme tous les effets d'optique non-linéaire, ne nécessite pas d'absorption : les électrons du milieu répondent de façon non-linéaire et quasi-instantanée à l'onde de pompe en convertissant celle-ci en ondes de fréquences différentes, mais ne sont pas excités à un niveau d'énergie supérieur. Les effets thermiques sont donc faibles dans un OPO (surtout en régime pulsé), à condition que le cristal utilisé soit très transparent.

Comment démarre un OPO : la fluorescence paramétrique

La fluorescence paramétrique est la lumière générée par la pompe en un passage à travers le milieu non-linéaire. Contrairement à la fluorescence d'un laser qui est incohérente et omnidirectionnelle, la fluorescence paramétrique est une lumière cohérente créée selon une ou plusieurs directions bien particulières dictées par l'accord de phase (voir ). Dans bon nombre d'OPO, cette fluorescence est d'intensité beaucoup trop faible pour être visible à l'œil nu, ou même détectable avec une photodiode.

D'après les équations de l'optique non-linéaire, cette fluorescence ne peut pas être créée à partir de rien : un bruit de départ est nécessaire. Ce bruit est appelé fluorescence paramétrique spontanée par analogie avec les milieux laser. Dans de nombreux travaux scientifiques, ce bruit, à défaut de pouvoir être mesuré, est modélisé par un champ phénoménologique dont l'énergie est celle d'un ou d'un demi photon par mode électromagnétique. On entend ici par mode une solution des équations de Maxwell dans le vide, avec les conditions aux limites imposées par exemple par la cavité optique de l'OPO. L'origine de ce bruit est encore discuté au sein de la communauté scientifique. Il est parfois attribué aux fluctuations quantiques du vide.

Un transfert d'énergie réversible : importance de la phase

Dans un OPO, les trois ondes pompe, signal, et complémentaires sont fortement couplées et échangent en permanence de l'énergie entre elles. Le sens de ce transfert d'énergie dépend fortement des phases et des intensités relatives de ces ondes. Par exemple, à forte puissance de pompe le signal et le complémentaire peuvent se recombiner pour générer de la pompe, et ainsi de suite. Cet effet de saturation limite la puissance générée et arrive souvent au centre d'un faisceau de pompe gaussien ou au sommet d'une impulsion.

Plus exactement, la génération paramétrique dépend de la phase non-linéaire . À chaque endroit z du milieu non-linéaire, l'intensité et les phases de chaque onde dépendent à la fois de l'intensité des deux autres ondes et de la phase non-linéaire ! Les équations non-linéaires gouvernant les amplitudes du champ électrique et les phases s'écrivent :

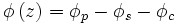
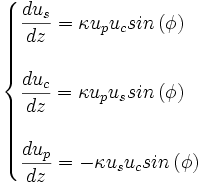
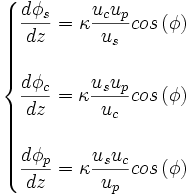
Lorsque la phase vaut π/2, les sinus valent 1, et est négatif : le transfert d'énergie se fait alors de la pompe vers le signal et le complémentaire. Pour une phase de -π/2, le transfert a lieu dans l'autre sens.

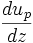
Au démarrage d'un OPO, la phase φ n'est pas déterminée car les ondes signal et complémentaire ne sont que du bruit. Lorsque leur amplitude augmente, leur phase s'ajuste afin que la phase non-linéaire vaille π/2 afin de privilégier le transfert d'énergie de l'onde la plus puissante vers les ondes les plus faibles. Si jamais la pompe tombe à zéro (dépeuplement complet), sa phase n'est plus définie. La phase non-linéaire s'ajuste alors à -π/2 pour maximiser le transfert vers l'onde la plus faible : il y a reconversion vers la pompe.

Dans un OPO simplement résonant (SROPO), la phase du signal doit respecter une condition de résonance dans la cavité optique. Elle doit revenir identique à elle-même sur un tour de cavité, soit : , où m est un entier relatif, L_s est la longueur optique d'un tour de cavité, et Δφ_s est le déphasage non-linéaire dû à la conversion paramétrique. Cette condition est réalisée pour un ensemble de modes équidistants en fréquence. Ces modes peuvent osciller s'il respectent la condition d'accord de phase, c'est-à-dire s'ils sont placés dans la courbe de gain de l'OPO, comme résumé sur la figure ci-contre. Comme le complémentaire n'est pas contraint par la cavité, sa phase s'ajuste automatiquement pour stabiliser la phase non-linéaire à π/2, là où le transfert d'énergie est le plus efficace, et donc là où le seuil de l'OPO est le plus bas. Ainsi il est toujours possible d'obtenir l'oscillation du signal avec un transfert de la pompe vers les deux autres ondes.

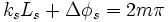
Dans un OPO doublement résonant (DROPO), les choses se compliquent puisque signal et complémentaires doivent tous deux osciller dans la cavité. Il y a donc deux conditions de phase à respecter :

Cette double condition doit également être compatible avec l'accord phase et la conservation de l'énergie. Un DROPO est donc un système surcontraint, ce qui rend l'oscillation possible que pour un nombre restreint de fréquences signal et complémentaire, appelées coïncidences. Ces coïncidences peuvent être partielles, ce qui donne lieu à des « paquets » de modes voisins oscillants, appelés clusters. Lorsque la longueur de la cavité fluctue légèrement (5 nm peuvent suffire), les peignes de fréquence signal et complémentaire se dilatent, et les coïncidences se retrouvent sur d'autres paires de modes. Ces sauts de modes peuvent se produire entre modes voisins ou d'un cluster à l'autre, ce qui entraîne de fortes instabilités de fréquence et d'intensité, en particulier lorsqu'il s'agit d'accorder l'OPO.

[conséquences sur la phase..]

Dans un DROPO en cavité linéaire, le signal et le complémentaire font un aller-retour dans le milieu non-linéaire pendant un tour de cavité. Au retour, l'accord de phase avec la pompe n'est pas possible puisqu'elle se propage dans la direction opposée. En l'absence de pompe, signal et complémentaire vont se combiner pour refaire de la pompe, selon le processus expliqué plus haut. Cette reconversion peut atteindre des valeurs aussi élevées que 20 % de l'énergie de pompe initiale.

Dans un SROPO ou une cavité en anneau (où les ondes ne circulent que dans un sens), les phénomènes de reconversion au retour n'existent pas, sauf en cas de réflexions parasites sur les optiques de la cavité (miroirs, faces du cristal...).

Qualité spatiale des faisceaux

Dans un laser, la qualité spatiale du laser est principalement déterminée par la cavité optique (et les effets thermiques dans le milieu laser) et non par la qualité du faisceau de pompe. En effet, l'énergie de la pompe est d'abord absorbée dans le milieu actif avant d'être restituée au faisceau laser par émission stimulée. Un laser peut donc être utilisé pour faire de la transformation de mode, c'est-à-dire générer un faisceau lumineux de bonne qualité spatiale à partir d'un faisceau de pompe de qualité moyenne.

Dans un OPO en revanche, les inhomogénéités spatiales du faisceaux de pompe sont fortement transmises aux ondes signal et complémentaire (avant d'être partiellement filtrées par diffraction dans la cavité). En effet, dans le milieu non-linéaire les trois ondes s'échangent de l'énergie de façon locale et quasi-instantanée. De plus, comme la conversion non-linéaire est d'autant plus importante que l'intensité est grande, les « points chauds » de la pompe auront tendance à être amplifiés. Cet effet est particulièrement important dans les OPO en régime impulsionnel, où les faisceaux sont peu filtrés par la cavité optique en raison du faible nombre d'aller-retours.

Effets thermiques dans un OPO

Comme l'énergie des ondes n'est pas stockée dans le milieu non-linéaire, les effets thermiques dans un OPO sont beaucoup plus faibles que dans un laser. Cependant, même les cristaux non-linéaires les plus purs possèdent une absorption résiduelle. De plus, la zone de transparence des cristaux est limitée en longueur d'onde. Ainsi, l'absorption du complémentaire au delà de 4 μm est une limitation bien connue des OPO à base de cristaux d'oxydes ferroélectriques tels que le niobate de lithium. Dans les OPO continus pour lesquels le seuil d'oscillation est élevé l'absorption résiduelle de la pompe devient non négligeable. Dans les OPO impulsionnels à fort taux de répétition (typiquement > kHz), la puissance moyenne absorbée peut devenir assez élevée pour créer une lentille thermique qui modifie la stabilité de la cavité. Les conséquences peuvent être : un profil spatial des faisceaux dégradé ou une instabilité en puissance (avec éventuellement une hystérésis en fonction de la puissance de pompe).