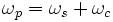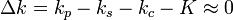Oscillateur paramétrique optique - Définition

Génération de la lumière dans un OPO

Lorsque le milieu non-linéaire est éclairé par un faisceau de lumière cohérente de fréquence ω_p, appelé faisceau de pompe, deux autres faisceaux sont produits : le faisceau signal de fréquence ω_s et le faisceau complémentaire de fréquence ω_c. Il n'existe pas de convention générale pour définir le signal par rapport au complémentaire (même si dans la majorité des publications sur le sujet le signal a la longueur d'onde la plus courte des deux). Les fréquences signal et complémentaire sont forcément inférieures à la fréquence de pompe, et doivent impérativement satisfaire la relation suivante :

Au cours de la propagation dans le milieu non-linéaire, l'énergie du faisceau pompe est transférée en faveur des faisceaux signal et complémentaire, si bien qu'on parle aussi de mélange ou de couplage à trois ondes. Le milieu non-linéaire se comporte donc comme un convertisseur de fréquence optique. Comme pour tous les phénomènes d'optique non-linéaire, ce phénomène n'apparait qu'à des densités de puissance lumineuse assez importantes, ce qui nécessite l'emploi d'un laser.

On décrit parfois ce processus en termes de photons (approche corpusculaire). Ainsi, chaque photon de pompe « se scinde » en deux autres photons. Si on se rappelle que l'énergie d'un photon est , où est la constante de Planck, la relation précédente ne traduit rien d'autre que la conservation de l'énergie. Ici, il ne faut pas confondre l'énergie individuelle des photons, qui traduit une fréquence, et celle des faisceaux en entier, qui traduit le flux lumineux (ou débit de photons).

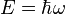
Cependant, cette relation seule n'impose pas les valeurs individuelles des fréquences signal et complémentaire, si bien qu'un nombre infini de possibilités semble exister. En réalité, les trois ondes mises en jeu doivent également respecter la relation d'accord de phase.

Accord de phase par biréfringence de forme

Dans certains matériaux isotropes, il est possible de créer une biréfringence artificielle grâce à une structuration particulière du milieu. Deux ondes polarisées perpendiculairement voyant alors des indices effectifs de propagation différents, l'accord de phase devient possible. Cette technique a été surtout appliquée aux semiconducteurs, qui bénéficient des techniques de croissance et de structuration développées à l'origine pour la microélectronique. Par exemple, des guides alternant des couches de GaAs (indice élevé de ~ 3,5) et de Al(Ga)As oxydé (Alox d'indice faible ~ 1,6) ont été créés, permettant notamment le doublage de fréquence à 1,6 µm et la génération paramétrique à 2,1 µm. De plus, la biréfringence artificielle ainsi créée peut être ajustée en modifiant la structure du milieu, ce qui permet de choisir les longueurs d'ondes émises.

Quasi-accord de phase

Dans certains cas, il n'est pas possible de trouver un pour les fréquences signal et complémentaire désirées. C'est le cas notamment des matériaux non-linéaires isotropes, comme l'arseniure de gallium GaAs. À défaut d'annuler exactement le désaccord de phase, il est parfois possible de le remettre à zéro périodiquement afin de garder les ondes en phase : c'est le quasi-accord de phase.

Pour cela, le signe de la non-linéarité du matériau doit être inversé toutes les longueurs de cohérence (voir figure ci-contre). Ceci équivaut à rajouter une phase de π au désaccord de phase, c'est-à-dire à renverser le sens du transfert d'énergie entre les ondes. Les interférences destructives qui ont normalement lieu à chaque longueur de cohérence sont supprimées, et la puissance des ondes générées peut croître continûment à la traversée du milieu non-linéaire (voir figure ci-contre). Cependant, l'efficacité est réduite d'un facteur (2/π)².

Si Λ est la période de retournement qui minimise le désaccord de phase, ce dernier s'écrit alors :

où est le vecteur du réseau formé par les domaines retournés.

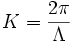
Il existe des variantes à ce quasi-accord de phase, comme l'inversion des domaines avec une période multiple de la longueur de cohérence, ou la modulation partielle de la non-linéarité, sinusoïdale par exemple. Le formalisme de Fourier permet de voir que toute modulation de la non-linéarité comportant une harmonique m du vecteur K est un quasi-accord de phase d'ordre m, plus ou moins efficace.

En plus de pouvoir remplacer l'accord de phase par biréfringence lorsque celui-ci n'est pas possible, le quasi-accord de phase possède un certain nombre d'avantages :

• Il n'est plus nécessaire d'avoir des ondes de polarisations croisées ;
• le (walk-off) entre les ondes est supprimé ;
• même pour les matériaux où il existe un accord de phase par biréfringence, le quasi-accord de phase peut permettre d'utiliser une direction de propagation dans laquelle la non-linéarité du matériau est plus importante.

Pour réaliser l'inversion périodique de la non-linéarité, il existe plusieurs techniques. Dans les cristaux ferroélectriques comme le niobiate de lithium, le phosphate de potassium titanyl (KTP) et le phosphate de rubidium titanyl (RTP), le retournement se fait par l'application d'un champ électrique très intense (voir figure ci-contre). La période du réseau ainsi créé peut aller de quelques dizaines de μm à quelques μm, la résolution de cette technique ne permettant pas de descendre plus bas. Si une période plus petite est nécessaire, il est possible d'appliquer très localement le champ électrique par un microscope à force atomique (AFM), ou bien de provoquer le retournement des domaines par un faisceau d'électrons focalisé (analogue à celui d'un microscope électronique à balayage), ce qui permet de descendre en dessous de 1 μm. En revanche, avec ces techniques l'ouverture des cristaux est généralement limitée à quelques mm, ce qui limite le diamètre des faisceaux pouvant s'y propager, et limite l'acceptance angulaire du cristal.

Une autre technique consiste à découper des plaquettes dans le matériau non-linéaire, puis à les coller ensemble en alternant l'orientation. Pour certains matériaux comme l'arseniure de gallium, l'alternance se fait lors de la croissance par épitaxie, grâce à des motifs déposés sur le matériau.

Les matériaux ainsi inversés sont renommés en y ajoutant le préfixe anglo-saxon « PP » pour periodically poled. Un des premiers matériaux ainsi réalisés est le niobate de lihitum périodiquement retourné, ou PPLN, réalisé par l'équipe de Matuo Yamada des laboratoires Sony à la fin des années 1990, puis par celle de Martin Fejer de l'Université de Stanford. Le PP-GaAs est également intéressant car il est fortement non-linéaire.

La nature vectorielle de l'accord de phase a permis d'envisager des techniques d'accord de phase où la non-linéarité est modulée suivant deux directions de l'espace. Ce sont ainsi des réseaux à deux dimensions qui sont créés dans les cristaux non-linéaires.

Le quasi-accord de phase peut aussi être réalisé en remettant les ondes en phase périodiquement, sans inversion du signe de la non-linéarité. Le quasi-accord de phase de Fresnel exploite par exemple le déphasage dit de Fresnel subi par une onde lorsqu'elle se réfléchit à l'interface entre deux milieux. En faisant propager les ondes en zig-zag dans une plaquette de matériau, il est ainsi possible de rattraper le déphasage à chaque réflexion sur les bords de la plaquette. Mais ceci n'est possible que pour certains angles de propagation.

À noter qu'il existe également un quasi-accord de phase pour lequel c'est la dispersion qui est modulée, donc les valeurs des indices vus par les trois ondes.