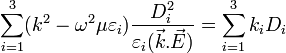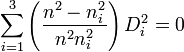Biréfringence - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
![](https://static.techno-science.net/illustration/Definitions/1200px/c/calcite_7fc1959623ab338bb579f27fb7f4a390.jpg")
La biréfringence est la propriété physique d'un matériau dans lequel la lumière se propage de façon anisotrope. Dans un milieu biréfringent, l'indice de réfraction n'est pas unique, il dépend des directions de propagation et de polarisation du rayon lumineux.
Un effet spectaculaire de la biréfringence est la double réfraction par laquelle un rayon lumineux pénétrant dans le cristal est divisé en deux. C'est pourquoi, sur la photographie ci-contre, l'inscription apparaît en double après avoir traversé le cristal de calcite. Ce phénomène est caractéristique des milieux biréfringents, à tel point que les termes « double réfraction » et « biréfringence » sont parfois confondus. Le second tire d'ailleurs son étymologie du premier.
Lorsqu'on parle de biréfringence, on sous-entend en général biréfringence linéaire, c'est-à-dire qu'on considère les indices de réfraction pour des ondes polarisées rectilignement. Par analogie, on utilise parfois l'expression biréfringence circulaire pour désigner l'activité optique. En effet, ces deux phénomènes peuvent se décrire de manière très similaire, mais ils ont des origines microscopiques différentes.
Dans le cas particulier des matériaux biréfringents uniaxes, on appelle également biréfringence la valeur de la différence entre les indices de réfraction extraordinaire et ordinaire du matériau (voir la définition de ces termes). La biréfringence peut ainsi être positive ou négative.
Historique
On attribue généralement au danois Rasmus Bartholin la découverte de la biréfringence du spath d'Islande. Ce minéral possède une biréfringence très forte qui permet des observations à l’œil nu, observations que Bartholin décrit dans son ouvrage « Experimenta crystalli Islandici » en 1670. En 1690, le physicien hollandais Christiaan Huygens suppose que pour l'une des images observées à travers le cristal, les rayons suivent un trajet ordinaire. Mais, pour la seconde image, le trajet des rayons n'obéit pas aux lois normales de la réfraction et il propose d'utiliser des ellipsoïdes comme surfaces d'ondes. Il découvre également que la double réfraction disparaît, lorsque les rayons réfractés dans le plan de section principale sont parallèles à la direction de l'axe optique du cristal.
Description mathématique, ellipsoïde des indices
L'indice de réfraction d'un milieu est lié à sa permittivité qu'on décrit mathématiquement par un tenseur d'ordre 2. Ce tenseur peut être représenté graphiquement par un ellipsoïde dont les longueurs des demi-axes sont les indices de réfraction principaux. C'est ce qu'on appelle l'ellipsoïde des indices. Cette construction graphique permet de visualiser la relation entre le champ électrique E et le déplacement électrique D ainsi que les directions des axes optiques.
Principe
Soit un milieu optiquement anisotrope. L'indice optique n correspondant à la direction du vecteur unitaire d'excitation électrique 
vérifie l'équation 
.
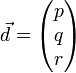
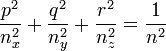
En notant x = n.p, y = n.q, z = n.r, on obtient l'équation de l'ellipsoïde des indices :
 |
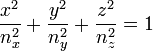
où x,y,z sont bien les coordonnées des points appartenant à un ellipsoïde. Les indices nx, ny et nz sont donnés par les composantes 
, 
et 
du tenseur de permittivité électrique du milieu dans ses axes propres, dans l'approximation d'un milieu non magnétique : 
(avec μr = 1 et 
)
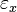
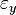
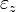
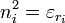
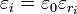
Il s'agit de travailler en cartésiennes pour exprimer les équations de Maxwell en fonction du vecteur 
. Une fois démontré que 
, on projette cette équation sur 
en utilisant 
. Les relations entre la vitesse de la lumière, l'indice optique et les permittivités électriques relatives et absolues permettent de conclure.
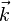
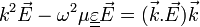
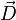
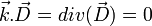
On effectue les approximations suivantes pour exprimer les équations de maxwell :
- pas de charge extrinsèque : ρex = 0 donc
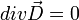
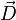
( étant le vecteur excitation électrique) - pas de courant extrinsèque :
donc 
(
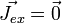
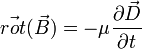
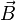
étant le vecteur champ magnétique) - milieu homogène et linéaire :
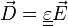
Il s'agit tout d'abord de calculer, en coordonnées cartésiennes, la quantité 
pour une onde plane progressive monochromatique de deux façons différentes. Cette quantité s'écrit 
.
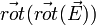
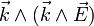
En utilisant les équations de Maxwell, on peut l'écrire 
.
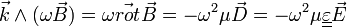
En utilisant les propriétés vectorielles du produit mixte, on peut l'écrire 
.
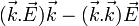
D'où l'équation de départ du raisonnement :
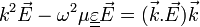
Plaçons-nous dans le référentiel propre du tenseur 
. Il s'assimile alors à une matrice diagonale 3*3. En indiçant par i les coordonnées cartésiennes (x,y,z) du repère, on obtient pour chaque coordonnée l'équation 
.
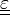
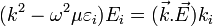
On divise ensuite l'équation par 
et on la multiplie par Di, sachant que 
. En sommant les 3 relations obtenues (une pour chaque coordonnée), on a
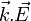
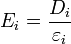
Le membre de droite correspond au produit scalaire 
, c'est-à-dire 
. Puisque le membre de gauche est nul, on peut éliminer le facteur et remplacer 
par 
qui lui est proportionnel. De même, en faisant apparaître la vitesse de la lumière dans le vide 
et sachant que 
(avec μr = 1 vu que le matériau est considéré non magnétique aux longueurs d'onde considérées), on obtient après avoir tout divisé par n2 :
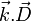
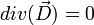
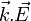
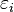
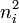
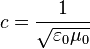
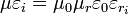
On peut encore écrire cette égalité 
. Introduisant maintenant le vecteur unitaire 
de coordonnées (p,q,r). En divisant l'égalité précédente par D2, on obtient .
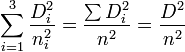
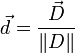
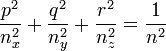
En notant x = n.p, y = n.q, z = n.r, on obtient l'équation de l'ellipsoïde des indices :
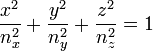
Interprétation physique
Considérons une onde plane électromagnétique. L'analyse vectorielle (en cartésiennes) des équations de Maxwell permet de conclure que les vecteurs suivants sont coplanaires :
- (excitation électrique) et donc le vecteur
dont les coordonnées interviennent dans l'équation de l'ellipsoïde 
(champ électrique)- (vecteur d'onde colinéaire à la direction de propagation de l'onde)
(vecteur de Poynting colinéaire à la direction de propagation de l'énergie)
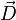
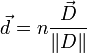
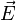
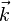
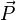
Le plan auquel appartiennent ces vecteurs est le plan de polarisation de l'onde. C'est le vecteur qui est perpendiculaire à dans les milieux matériels, et non comme c'est habituellement le cas dans le vide.
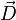
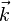
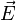
De plus, on montre que le vecteur est normal à l'ellipsoïde au point d'intersection avec 
.
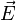
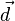
Le vecteur normal à l'ellipsoïde en un de ses points de coordonnées (x,y,z) est 
où l'équation de l'ellipsoïde est f(x,y,z) = 0. Le vecteur gradient au point considéré est 
où (x,y,z) sont les coordonnées du vecteur . Chacune de ses composantes di (
) est reliée à par 
et les composantes de sont reliées à celles de par 
où 
.
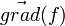
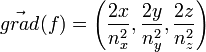
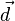
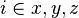
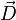
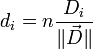
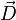
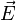
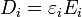
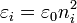
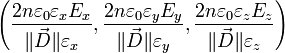
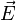
est donc perpendiculaire à la surface au point (x,y,z), et par conséquent, le vecteur également.Tenant compte de cette condition et de la coplanarité de , et , seules deux orientations sont géométriquement permises pour . En effet, l'intersection du plan d'onde (plan perpendiculaire à , auquel appartient donc ) avec l'ellipsoïde est une ellipse. Les conditions géométriques sont remplies dans 2 cas : lorsque est selon le petit axe et lorsqu'il est selon le grand axe de cette ellipse.
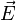
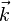
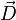
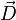
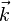
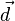
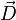
- Lorsque est colinéaire à , on parle de rayon "ordinaire". Rien de spécial n'arrive au rayon lumineux
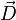
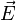
- Il existe une autre configuration, qui donne lieu à un rayon extraordinaire. Cette dénomination lui est donnée en raison de la violation des lois de Snell-Descartes par ce rayon. Cette violation n'est pas paradoxale, car les lois de Descartes découlent elles-mêmes des équations de Maxwell dans un cas précis (l'isotropie cristalline), qui, elles, sont toujours vérifiées dans le cas de la biréfringence.