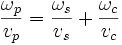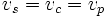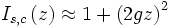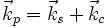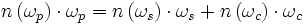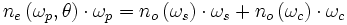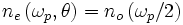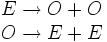Oscillateur paramétrique optique - Définition

Comment fonctionne un OPO : l'accord de phase

Importance de l'accord de phase

La conversion de la pompe vers les faisceaux générés n'est efficace que si les vitesses de phase v des ondes respectent la relation suivante :

La signification de cette relation apparaît plus clairement dans le cas particulier de la dégénérescence, pour lequel signal et complémentaire sont de fréquences identiques, ω_s = ω_c = ω_p/2 :

Sans cette condition, les ondes générées au cours de la propagation dans le milieu non-linéaire se déphasent et finissent par interférer de façon destructive : la puissance résultante est très faible. Lorsque l'accord de phase est réalisé, les ondes interfèrent de façon constructive, et la puissance générée varie comme le carré de la longueur du milieu non-linéaire :

où g est le gain paramétrique, proportionnel à la non-linéarité du milieu et à l'amplitude de l'onde de pompe.

Cette relation d'accord de phase peut également s'écrire sous une forme plus générale, en fonction des vecteurs d'onde :

Si on se rappelle que l'impulsion d'un photon est , la relation précédente ne traduit rien d'autre que la conservation de la quantité de mouvement des photons. Comme il s'agit d'une relation vectorielle, cela signifie qu'il peut exister des accords de phase non colinéaires, c'est-à-dire pour des faisceaux pompe, signal et complémentaire se propageant dans des directions différentes.

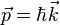
Contrairement à la conservation de l'énergie, l'accord de phase est une condition qui ne se réalise pas toute seule. En effet, dans le milieu non-linéaire, les vitesses de phase des trois ondes sont différentes, car leurs fréquences sont différentes. Cette propriété générale des milieux matériels est la dispersion. Le rôle de la dispersion apparait plus clairement si la relation d'accord de phase est réécrite en introduisant les indices de réfraction ou indices optiques n des ondes, :

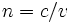
Cette égalité semble impossible puisque et qu'en plus les trois ondes doivent respecter la conservation de l'énergie, . En réalité, dans certains matériaux, appelés biréfringents, ou anisotropes, l'indice de réfraction dépend également de la polarisation. Grâce à ce degré de liberté supplémentaire, il est possible de réaliser l'accord de phase entre des ondes de fréquences différentes, à condition que leurs polarisations soient judicieusement choisies. Dans les milieux non-linéaires isotropes en revanche, ce type d'accord de phase n'est pas possible : c'est la technique du quasi-accord de phase qui est alors utilisée.

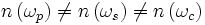
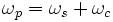
La découverte de l'accord de phase par biréfringence est généralement attribuée à Joseph A. Giordmaine et Paul D. Maker en 1962. Le quasi-accord de phase a été imaginé par Nicolaas Bloembergen et John Armstrong en 1962 ainsi qu'indépendamment par P. A. Franken et J. F. Ward la même année.

Accord de phase par biréfringence

Pour comprendre l'accord de phase par biréfringence, prenons l'exemple du cristal non-linéaire de Beta Borate de Baryum β-BaB₂O₄ (BBO). Ce cristal possède deux indices optiques selon la polarisation de la lumière : un indice ordinaire n_o(ω) pour une certaine polarisation O de la lumière, et un indice extraordinaire n_e(θ, ω) pour la polarisation E perpendiculaire. L'indice ordinaire ne dépend pas de la direction de propagation θ des ondes lumineuses, exactement comme dans un cristal isotrope. L'indice extraordinaire, lui, en dépend. Dans ce cristal, si l'onde pompe est polarisée E et se propage avec un certain angle θ, elle peut être convertie efficacement en une onde signal et une onde complémentaire toutes deux polarisées O. On note ce processus de la manière suivante : . La relation d'accord de phase est donc possible et s'écrit dans ce cas :

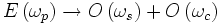
Dans le cas simple de la dégénérescence, réaliser l'accord de phase signifie trouver la direction de propagation θ telle que l'onde pompe extraordinaire ait le même indice (i.e. la même vitesse de phase) que l'onde ordinaire générée :

De manière générale, on distingue les accord de phase de type I, où signal et idler sont polarisés de la même manière :

et les accords de phase de type II où ces deux ondes ont leur polarisations croisées :

Ces deux types d'accords de phase peuvent exister simultanément dans un même cristal, et ont chacun des avantages et des inconvénients que nous ne détaillerons pas ici.

Cône de fluorescence paramétrique

Une autre façon de voir l'importance de l'angle de propagation des ondes dans les effets non-linéaires est ce qu'on appelle le cône de fluorescence paramétrique. Prenons le cas d'un cristal non-linéaire sans cavité optique, éclairé par une onde pompe de très forte intensité. Un accord de phase non colinéaire sera trouvé pour un couple de fréquences (ω_s, ω_c) correspondant à des directions de propagations des ondes (k_s, k_c), la direction de la pompe kp étant fixée. Un autre accord de phase existe pour un autre couple de fréquences (ω_s', ω_c') correspondant à des directions différentes (k_s', k_c'), et ainsi de suite. Il en résulte la génération de deux cônes de lumière superposés, un cône signal et un cône complémentaire. Pour une pompe ultraviolette à 351 nm, le cône signal est majoritairement dans le visible et le cône complémentaire dans l'infrarouge.