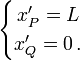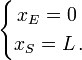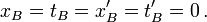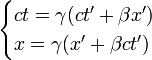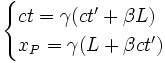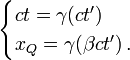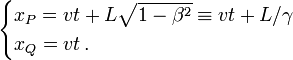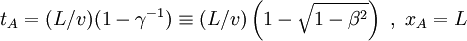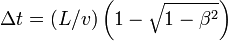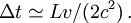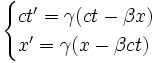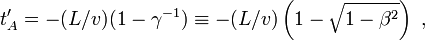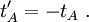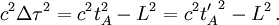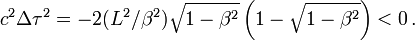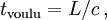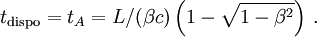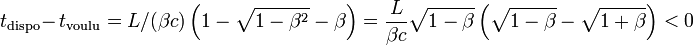Paradoxe du train - Définition
La liste des auteurs de cet article est disponible ici.
Calcul algébrique
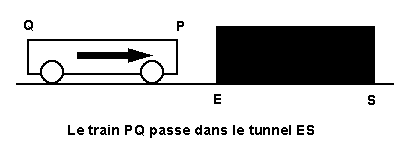
Considérons un train PQ de longueur propre L, P étant l'avant et Q l'arrière. Si on choisit l'arrière du train comme origine des coordonnées spatiales dans ce repère, les abscisses des extrémités sont :
Considérons maintenant un tunnel ES de même longueur L que le train mesurée dans le repère fixe. E est l'entrée du tunnel, S la sortie. Dans ce repère « fixe », l'entrée du tunnel est prise comme origine des coordonnées spatiales de sorte que les abscisses de E et S sont
Le temps dans le repère du train sera mesuré par la quantité t ’, et dans le repère de la voie par la quantité t.
L'événement « émission du signal B », celui qui marque la coïncidence du point Q avec E, c'est-à-dire l'entrée de l'arrière du train dans le tunnel) sera pris comme origine des coordonnées. Par convention on a donc :
L'événement « émission du signal A », qui marque la coïncidence de P avec S, c'est-à-dire la sortie de l'avant du train, est déterminé par
-
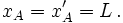
Si la vitesse du train est v par rapport aux observateurs fixes situés sur la voie ferrée, les formules de Lorentz, qui permettent de passer des coordonnées (x ’, t ’) mesurées dans le train aux coordonnées (x, t ) mesurées sur la voie, s'écrivent :
où β et γ sont les quantités usuelles
-
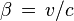
![\gamma\,=[1 - (v^2/c^2)]^{-1/2}\equiv 1/\sqrt{1-\beta^2} \,.](https://static.techno-science.net/illustration/Definitions/autres/9/9ce64385f1093409f2ef6921ef969d6a_c20634c81190b7f44cd4e4b68330eb15.png)
![\gamma\,=[1 - (v^2/c^2)]^{-1/2}\equiv 1/\sqrt{1-\beta^2} \,.](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/9ce64385f1093409f2ef6921ef969d6a_c20634c81190b7f44cd4e4b68330eb15.png)
D'après les formules précédents les coordonnées des extrémités P et Q du train dans le repère de la voie ferrée s'expriment sous la forme :
et
En éliminant t ' dans ces équations on aboutit à l'équation du mouvement de P et Q dans le repère fixe de la voie :
Incidemment on retrouve le facteur de contraction des longueurs de Lorentz 1/γ en vérifiant qu'au même instant t (par exemple en t = 0) la différence (x - x), qui représente la longueur du train dans le repère fixe, est égale à L /γ.
Les équations précédentes fournissent alors les coordonnées temporelle et spatiale de l'événement A comme
Comme annoncé on constate que depuis la voie l'instant t du signal A de sortie du tunnel est postérieur à l'instant du signal indiquant l'entrée dans le tunnel de la queue du train (le train est plus court que le tunnel). La différence de temps entre les deux événements A et B est
Lorsque β est assez petit on peut développer l'expression au premier ordre pour obtenir
Comment les choses se mesurent-elles dans le repère du train ? Les formules inverses permettant de passer des coordonnées fixes aux coordonnées mobiles (pour dire les choses rapidement) sont :
Après un calcul identique au précédent on obtient les coordonnées de l'événement A dans le repère du train comme
On constate que l'ordre temporel des événements est inversé dans le repère du train par rapport au repère de la voie. Maintenant t ’ est négatif, ce qui signifie que l'avant du train sort du tunnel avant que l'arrière y soit entré (pour les voyageurs le tunnel est plus court que le train). La situation est parfaitement symétrique puisque
Tout est cohérent. Le paradoxe du train dans le tunnel n'est pas signe que la relativité restreinte serait fausse.
Revenons enfin à la question de savoir si la bombe prête à exploser quand le train sort du tunnel le fera ou non. Calculons à cet effet le carré de l'intervalle spatio-temporel
On trouve
Cette quantité est le fameux invariant de la relativité restreinte, c'est-à-dire qu'elle ne dépend pas du repère dans lequel on la calcule. Elle reste notamment négative quel que soit le repère considéré, ce qui montre que les deux événements A et B ne peuvent pas être liés par un lien de cause à effet, dans aucun repère. L'intervalle d'espace-temps entre les deux événements A et B est dit du « genre espace ».
Vérifions directement en faisant le calcul dans le repère de la voie que le signal de désamorçage B n'a pas le temps d'atteindre l'avant du train avant l'explosion de la bombe. Le temps nécessaire pour que le signal (voyageant à la vitesse c) aille de l'arrière à l'avant est
tandis que le temps disponible est
On constate que
Le fait que le temps disponible soit inférieur au temps nécessaire signifie bien que le signal B n'a pas le temps d'atteindre la bombe pour la désamorcer avant qu'elle explose.
Dans les deux repères la conclusion est la même : les deux événements « explosion de la bombe » et « envoi du signal de désamorçage » sont causalement indépendants. Par conséquent les passagers du train comme les observateurs fixes de la voie concluent que la bombe explosera.
