Pedro Nunes - Définition

Œuvres

Le commentateur

Pedro Nunes vivait dans une époque de transition où l'activité scientifique, jusqu'alors consacrée à la préservation et à la propagation des connaissances traditionnelles (commentaires des Anciens), commençait à se tourner systématiquement vers les applications techniques de ces connaissances même. Il s'agissait donc de collecter des mesures et des observations permettant d'utiliser les théories existantes : au cours de ce processus, les limites d'application des idées des Anciens apparurent graduellement, amenant les commentateurs à tenter d'en rendre raison. Nonius fut d'abord l'un des derniers grands glossateurs des œuvres anciennes, ce que reflète le premier livre qu'il fit paraître. Dans son « Tratado da sphera », où il signale la valeur heuristique de l'expérimentation, il milite également pour une diffusion universelle du savoir : aussi ne se borna-t-il pas à publier ses écrits en latin, qui était alors la lingua franca de la science en Europe, mais aussi en langue vernaculaire (espagnol et portugais), comme son « Livro de Algebra ».

Le cartographe

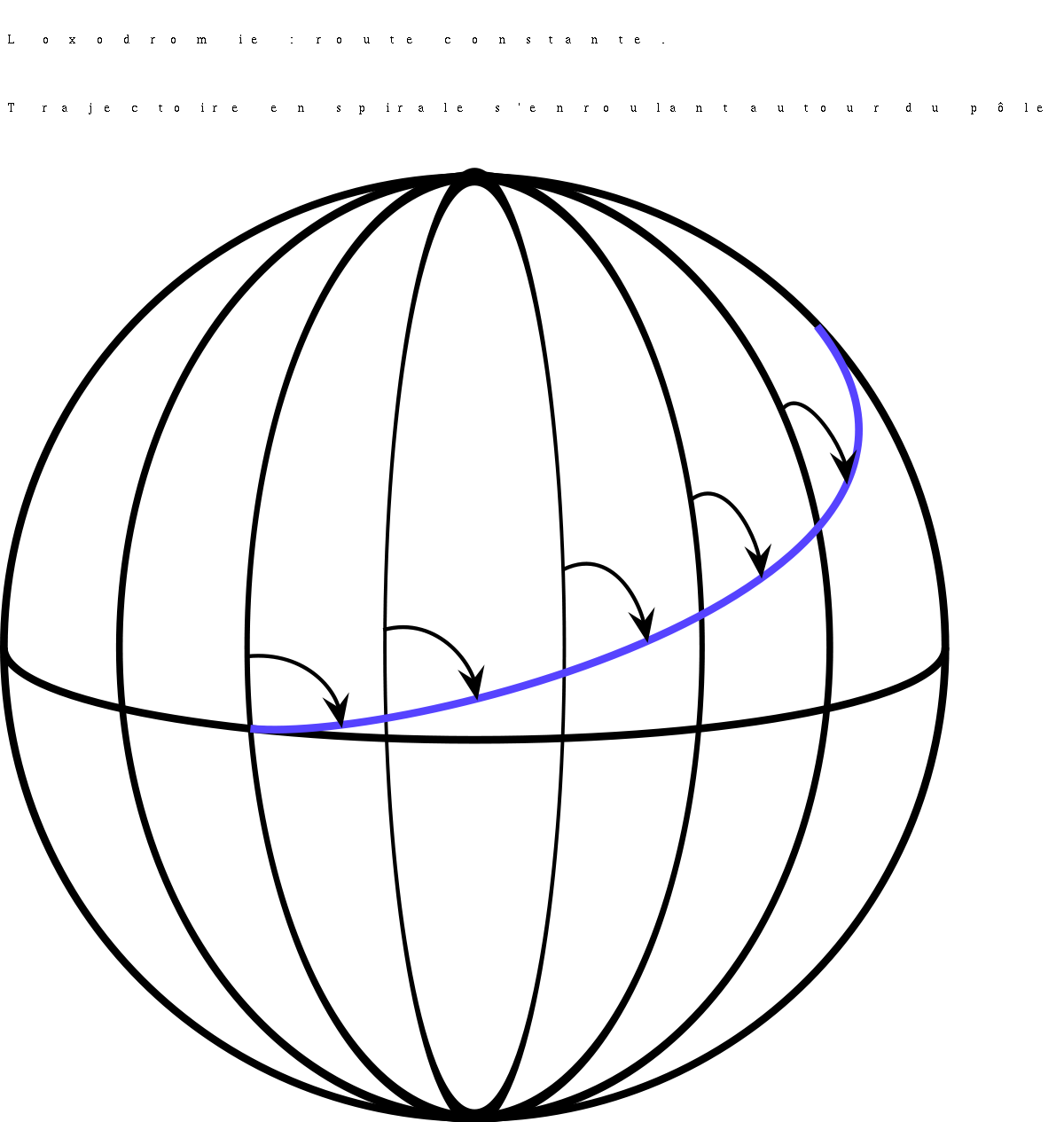
La plupart des ouvrages de Nunes sont consacrés à la navigation. Il fut le premier à expliquer pourquoi un vaisseau qui maintient son cap ne décrit pas un grand cercle (c'est-à-dire une géodésique de la sphère), mais plutôt une courbe spirale, qu'il appela loxodrome. Il fallut cependant attendre les travaux de Leibniz pour qu'à l'aide des logarithmes, la nature de la loxodrome soit établie.

Dans son « Éloge des cartes de marine », Nunes posa en principe qu'une carte nautique doit représenter les parallèles et les méridiens comme des lignes droites. Cependant, il ne parvint pas à résoudre tous les problèmes que posait cette exigence si l'on voulait en outre préserver les directions : le problème de la projection conforme ne fut résolu qu'avec la carte de Mercator et les travaux mathématiques de Wright et Harriot. Nunes se consacra au problème des longitudes, au repérage en mer et au calcul des corrections géographiques. Pour améliorer l'alidade des astrolabes, il imagina le nonius, ancêtre du vernier : ce dispositif est composé d'un faisceau de cercles concentriques, divisés avec un nombre de divisions croissant de l'intérieur vers l'extérieur (une division supplémentaire à chaque cercle). Ainsi, avec un quadrant extérieur divisé en 90 degrés, le deuxième cercle en allant vers l'intérieur n'en a plus que 89, le suivant 88, etc. Lorsque l'on mesure un angle, on relève le cercle et la division du cercle sur lesquels pointe l'alidade. Une table donne alors par conversion la mesure exacte des coordonnées du point. Le nonius fut longtemps utilisé par Tycho Brahe qui le trouvait trop fastidieux . Ce système fut perfectionné par Christopher Clavius et Jacob Curtius, jusqu'à ce que Pierre Vernier arrive à une solution satisfaisante.

Pedro Nunes s'attaqua également à l'étude mathématique des machines simples (plan incliné, roue, levier).

Astronomie et mathématiques

Dans ses exposés du système géocentrique de Ptolémée, Nunes évoque bien la théorie de Copernic, mais uniquement pour y signaler des erreurs de calcul. Nunes détermina la date où le crépuscule a la plus courte durée selon l'endroit de la Terre où l'on se trouve. Ce problème d'extrémum, s'il n'a pas en soi une grande importance, donne cependant une idée des capacités du mathématicien de Coimbra, dans la mesure où, encore plus d'un siècle plus tard, Jean et Jacques Bernoulli éprouvèrent les plus grandes difficultés à le résoudre : ils parvinrent bien à trouver la date de plus court crépuscule mais, se perdant dans des calculs de dérivée, ne purent calculer la durée même du plus court crépuscule. La solution de Nunes est, naturellement, complètement géométrique.

Les découvertes mathématiques de Nunes s'expliquent principalement par sa compréhension profonde de la trigonométrie sphérique et sa capacité à y appliquer les principaux énoncés de la géométrie euclidienne.