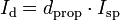Propergol liquide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En astronautique, on appelle propergol liquide tout système chimique composé d'un ou plusieurs ergols stockés à l'état liquide pour produire, par décomposition ou par combustion, un mélange gazeux dont la détente à travers une tuyère fournit une force de poussée. De tels propergols ne permettent pas d'atteindre des vitesses très élevées mais offrent une poussée suffisante pendant le temps nécessaire pour s'affranchir de la pesanteur et placer des charges utiles en orbite. Ils sont donc couramment utilisés pour fournir l'impulsion nécessaire au décollage des lanceurs et pour les manœuvrer dans l'espace.
Grandeurs caractérisant un propergol
Ces grandeurs sont introduites dans l'article "Moteur-fusée".
Impulsion spécifique
Notée Isp et mesurée en secondes, l'impulsion spécifique indique la durée pendant laquelle une masse d'un kilogramme de propergol peut fournir une force de poussée d'un kilogramme-force, soit 9,80665 N :
-
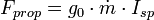
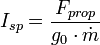
avec :
-
- Isp l'impulsion spécifique exprimée en secondes
- Fprop la force de poussée du propergol, mesurée en Newton
- g0 l'accélération de la gravité à l'équateur, soit 9,80665 m/s2
-
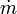
Cette équation souligne que, à poussée égale, l'impulsion spécifique sera d'autant plus élevée que le débit massique sera faible, ce qui signifie qu'on privilégiera des ergols dont les produits de combustion ont une masse molaire faible.
L'impulsion spécifique n'est pas une grandeur absolue d'un propergol, mais dépend des performances du moteur-fusée, et tout particulièrement de la pression atteinte dans la chambre de combustion, qui peut affecter les performances du système de 10 à 15 %. Elle dépend également de la détente des gaz d'échappement dans la tuyère, dont la géométrie doit être optimale pour maximiser la poussée, et elle dépend donc aussi de la pression à l'extérieur de la fusée : l'impulsion spécifique est maximale dans le vide, mais est inférieure près de 15 % au décollage au niveau de la mer.
Dans la littérature, les valeurs d'impulsion spécifique sont données dans le vide et dans les conditions thermodynamiques idéales, de sorte qu'elles constituent des bornes supérieures auxquelles les valeurs pratiques sont généralement inférieures de 5 à 10 %.
Vitesse d'éjection des gaz d'échappement
Dans la mesure où le rapport de la force de poussée au débit massique est égal à la vitesse d'éjection des gaz d'échappement, on peut également exprimer l'impulsion spécifique d'un propergol au moyen de la vitesse d'échappement, exprimée en mètres par seconde, selon l'égalité :
avec :
-
- ve la vitesse d'éjection des gaz d'échappement, exprimée en m/s
- g0 l'accélération de la gravité à l'équateur, soit 9,80665 m/s2
- Isp l'impulsion spécifique mesurée en secondes
Fraction massique du propergol, delta V, densité d'impulsion
Fraction massique
On appelle fraction massique du propergol le rapport entre la masse finale du lanceur (après combustion du propergol) et sa masse initiale (avec le propergol avant sa combustion) :
avec :
-
- fmass la fraction massique du propergol consommé, exprimée en kg
- mprop la masse de propergol consommé, mesurée en kg
- M0 la masse initiale de l'engin spatial (avec le propergol consommé), mesurée en kg
C'est une grandeur qui dépend à la fois de la conception du lanceur et de la densité du propergol employé.
Delta v
Par ailleurs, on désigne couramment par « delta v » le surcroît de vitesse imprimé à un engin spatial par la combustion d'une quantité donnée de propergol. En l'absence de champ de gravité et de frottements, l'équation de Tsiolkowski permet d'exprimmer simplement le delta V à partir de la fraction massique du propergol :
avec :
-
- Δv la variation de vitesse de l'engin spatial exprimée en m/s
- ve la vitesse d'éjection des gaz d'échappement, mesurée en m/s
- Mplein la masse de l'engin spatial au décollage, mesurée en kg
- Mvide la masse hors propergol de l'engin spatial, mesurée en kg
On voit clairement avec cette expression que, pour maximiser le delta v, il faut :
- utiliser un propergol qui permette d'éjection des gaz d'échappement à une vitesse ve aussi élevée que possible
- maximiser le rapport Mplein / Mvide, ce qui signifie :
-
-
- construire un astronef aussi léger que possible
- utiliser un propergol aussi dense que possible
-
Le delta v dépend donc à la fois de la masse du véhicule spatial et des qualités intrinsèques (masse volumique et vitesse d'éjection) du propergol utilisé.
Densité d'impulsion
La densité apparente du propergol étant une donnée aussi déterminante que son impulsion spécifique, on définit l'impulsion-densité (ou densité d'impulsion) comme le produit de ces deux grandeurs :
avec :
-
- Id l'impulsion-densité exprimée en s•kg/m3
- dprop la densité apparente du propergol mesurée en kg/m3
- Isp l'impulsion spécifique mesurée en secondes
C'est parfois le couple (Isp, Id) plutôt que le couple (ve, dprop) qui est indiqué dans les tables de valeurs numériques sur les propergols liquides.

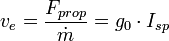
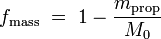
![\Delta{v}=v_{e}\cdot\ln\left[{\frac{M_\mathrm{plein}}{M_\mathrm{vide}}}\right]](https://static.techno-science.net/illustration/Definitions/autres/b/b8d370c6396d68999affb4a806b00ff1_6f1bdd0dc65cd81f20d3df0ae1aca29d.png)