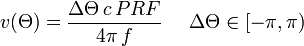Radar Doppler pulsé - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un radar Doppler pulsé est un radar capable, non seulement de donner le cap, la distance et l'altitude d'une cible, mais aussi de mesurer sa vitesse radiale (portée-vitesse). Pour cela il utilise l'effet Doppler. Le retour des impulsions radioélectriques renvoyées par réflexion sur la cible sont traitées pour calculer le glissement de fréquence entre l'onde émise et celle qui est reçue. Pour cela, le système d'émission doit avoir une excellente stabilité de phase, on dit, dans ce cas, qu'il est « cohérent ».
La nature même des radars pulsés, et la relation qui existe entre la fréquence de la porteuse et la fréquence de répétition des impulsions radar (ou PRF pour Pulse repetition frequency) font que le spectre de fréquence peut être très complexe et risque de conduire à des erreurs. En général pour éviter le crénelage on choisit une fréquence d'impulsion très élevée, mais ce choix peut occasionner des effets secondaires comme l'affichage de plusieurs distances pour une seule cible. Pour éviter cela, on utilise plusieurs fréquences d'impulsions différentes.
Principe de base
Le radar pulsé Doppler est basé sur deux prémisses. La première est que la position de la cible peut être calculée en notant le temps entre l'émission d'une impulsion radar et son retour de la source. La seconde sur le fait qu'une cible qui se déplaçant avec une vitesse radiale non–nulle par rapport au faisceau radar provoque un glissement de fréquence entre la fréquence de référence de l'émetteur et celle de la porteuse reçue après reflexion sur la cible.
Position

Entre chaque impulsion, l'antenne et le circuit électronique sont mis à l’écoute de l’impulsion de retour. On calcule la distance entre le radar et la précipitation par la relation suivante:
-
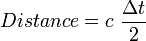
La distance maximale qu'on peut sonder sans ambiguïté dépend du
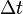
Vitesse
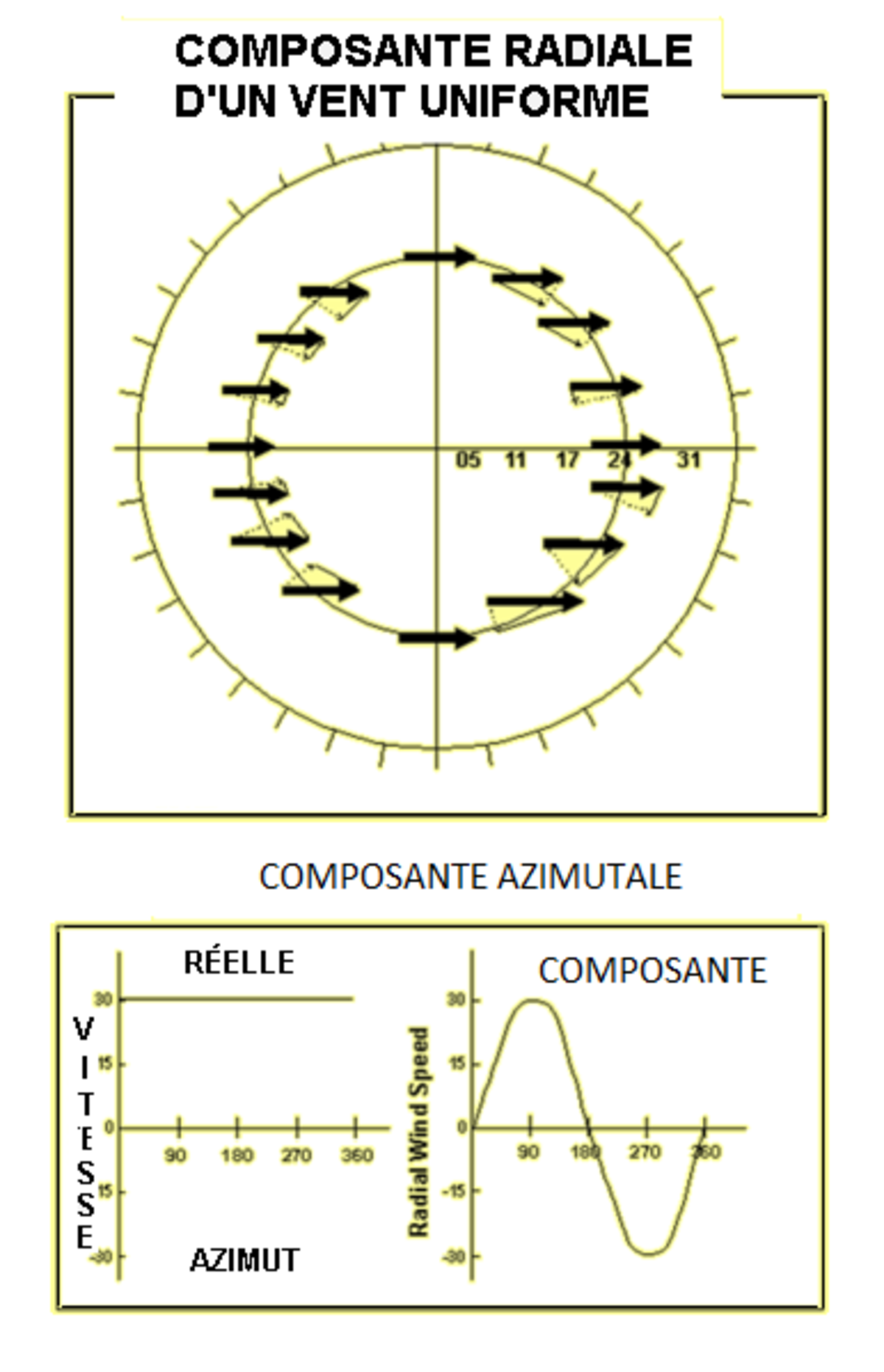
La différence de fréquence entre le faisceau émis et celui retourné est due à l'effet Doppler de telle sorte que les cibles se rapprochant donneront une fréquence apparente plus élevée alors que les cibles s'éloignant de l'émetteur restitueront une fréquence apparente plus basse. Toute cible se déplaçant tangentiellement au radar ne produira aucune variation de fréquence.
Le déplacement d'une cible pouvant être décomposée en portion parallèle et tangentielle, la variation mesurée n'est donc pas nécessairement reliée à la vitesse réelle mais seulement à celle de la composante radiale du déplacement (cosinus du déplacement par rapport à l'axe du faisceau). Cette vitesse radiale de la cible peut être estimée en déterminant le glissement de fréquence moyen de la porteuse à l'intérieur d'un groupe d'impulsions. En général, on utilise pour cela, soit une transformée de Fourier rapide, soit la technique de l'autocorrélation. La transformée est effectuée de façon indépendante pour chaque échantillon en utilisant des données reçues à la même distance à partir de toutes les impulsions d'un paquet ou d'un groupe de paquets. Dans les systèmes plus anciens on utilisait une série de filtres analogiques.
La cible doit être soit entrante vers le radar, soit sortante sinon les données obtenues seront classées dans un dossier réservé aux signaux mal ou pas interprétés. Si les informations de vitesse proviennent d'un seul radar, elles conduiront à sous-estimer la vitesse réelle. Une interprétation exacte du profil de la vitesse pour des cibles uniques nécessite la mise en œuvre de plusieurs radars situés à des endroits différents pour déterminer l'angle d'incidence. Dans le cas de cibles volumiques, comme la précipitation, se déplaçant à l'unisson et qui recouvrent une bonne partie de la zone couverte par un radar, une analyse des vitesses radiales sur 360 degrés autour d'un seul radar permet de déduire la vitesse et la direction de ces cibles en éliminant l'indétermination.
La vitesse radiale de la cible peut être facilement calculée dès lors que l'on connait la fréquence du radar (f), la vitesse de la lumière (c), la fréquence de répétition des impulsions (PRF) et le décalage moyen en fréquence (
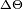
Démodulation du signal
L'image reçue finale est formée par des filtres de vitesse doppler ou des circuits de traitement numérique du signal. La plupart des radars doppler pulsés modernes possèdent un étage de démodulation du signal entrant qui centre la fréquence sur zéro, en retirant la fréquence porteuse, avant l'échantillonnage numérique. Ceci a pour effet de diminuer la puissance de calcul nécessaire (le taux d'échantillonnage étant réduit d'autant) et la capacité de stockage. Le signal résultant est souvent appelé IQ-data où IQ signifie « en phase » et « en quadrature de phase » pour rappeler que le signal est représenté par un nombre complexe avec une partie réelle et une partie imaginaire.
Par exemple, un signal modulé S(t) = cos(ω0t + φ(t)) pourra être démodulé en utilisant :
- IH(t) = S(t).cos(ω0t) et QH(t) = S(t).sin(ω0t)
En utilisant un filtre passe-bas à la fois sur IH(t) et QH(t) on obtiendrait :
- I(t) = cos(φ(t) + Φ) et Q(t) = sin(φ(t) + Φ)
Notons que I(t) seul ne serait pas suffisant car le signe resterait indéterminé. Avec I(t) et Q(t) le radar peut discriminer les vitesses doppler entrantes et sortantes.