Ressort à lames - Définition

Introduction

Ressort à lames utilisé pour la suspension automobile

Un ressort à lames est un type de ressort où l'on utilise la flexibilité d'une ou plusieurs lames métalliques superposées et leur propriétés élastiques pour absorber l'énergie mécanique, produire un mouvement, exercer un effort ou un couple sur système. On compte deux configuration d'usage: une extrémité des lames est fixe et l'autre subit la force à restituer ou les deux extrémités sont fixes et la force à restituer s'exerce au centre des lames.

Ce type de ressort est surtout utilisé pour la suspensions de véhicules afin de ramener les roues dans leur position initiale après une bosse ou un cahot (deux extrémités fixes). C'est aussi le dispositif retenu en organologie pour la réalisation des ressorts de rappel de certaines clefs d'instruments à vent comme la clarinette (une extrémité fixe).

Forme de base

Nous nous contenterons ici d'un calcul de prédimensionnement (on dit parfois d' « équarrissage ») permettant de se faire une idée approximative de l'encombrement qu'aurait un véritable ressort à lames réalisé selon les règles de l'art. Une lame encastrée à une extrémité et chargée à l'autre peut évidemment servir de ressort mais les contraintes maximales règnent du côté de l'encastrement tandis que l'extrémité libre, qui a le même module de flexion I/v que l'autre, est peu sollicitée.

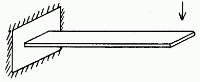
Pour mieux utiliser la matière, on cherche évidemment à se rapprocher d'une forme d'égale résistance qui est dans ce cas de figure une forme de largeur constante et de hauteur variant selon une loi parabolique (solution utilisée par exemple sur le TRAFIC de Renault), ou bien une lame triangulaire de hauteur constante, qui va nous servir de base de calcul.

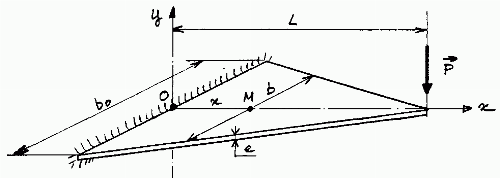
Si b_o est la largeur de cette lame au niveau de l'encastrement et L sa longueur, la largeur de la lame au point M d'abscisse x s'écrit :

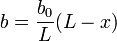
Le moment de flexion en M est

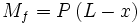
La contrainte maximale de flexion est constante tout au long de la lame :

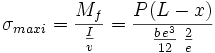
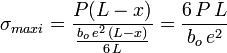
Condition de déformation

Dans l'hypothèse, classique mais ici irréaliste, des petits déplacements, nous pouvons calculer la flèche f de l'extrémité libre sous l'effet de la charge P :

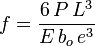
Les deux conditions de résistance et de déformation imposent ensemble l'épaisseur maximale de la lame :

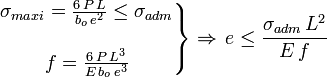
Une fois l'épaisseur arrondie à une valeur normalisée, il en résulte la détermination de b_o, qui donne généralement des dimensions prohibitives pour la lame.

Condition de résistance

Elle découle du calcul précédent :

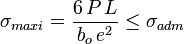
Quelques problèmes de réalisation

Les formes réelles seront assez éloignées de la forme théorique d'égale résistance que nous venons de voir :

• la plus longue lame, ou lame maîtresse, doit avoir une section suffisante pour résister seule à l'effort tranchant, ainsi que pour permettre la liaison avec les éléments extérieurs. Son extrémité n'est donc jamais triangulaire mais toujours façonnée en fonction des besoins.

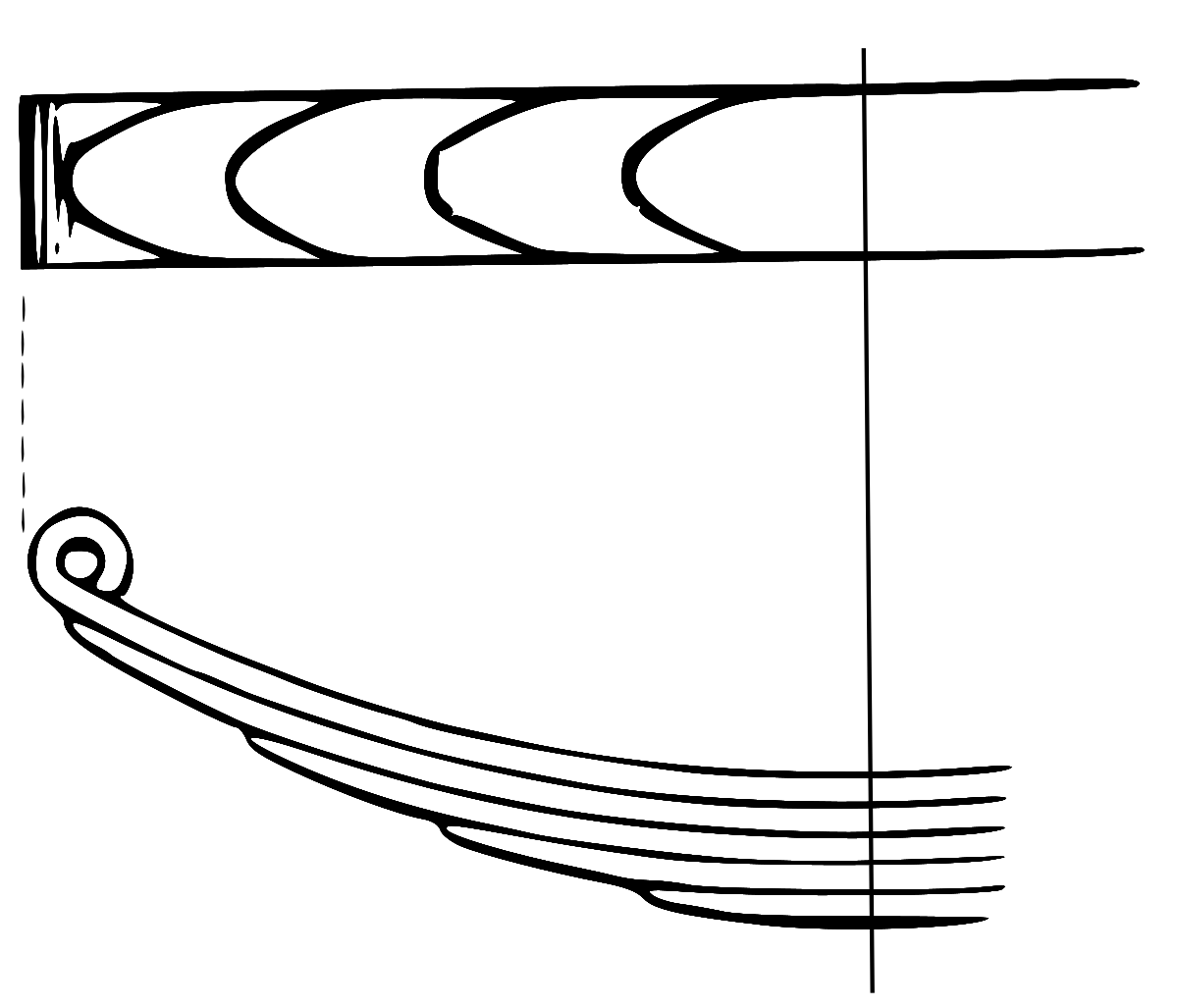
• pour éviter que le ressort « baille », c'est-à-dire que les lames décollent, on donne à ces dernières une courbure qui croît de la lame maîtresse, la plus longue, aux plus courtes. Il faut alors que les épaisseurs des lames aillent en décroissant, sinon on dépasserait de plus en plus largement la limite d'élasticité.

• l'extrémité des lames n'est jamais taillée en pointe, mais coupée droite, terminée en trapèze ou encore amincie et arrondie selon un profil parabolique.

lames droites

lames trapézoïdales

lames à extrémités paraboliques

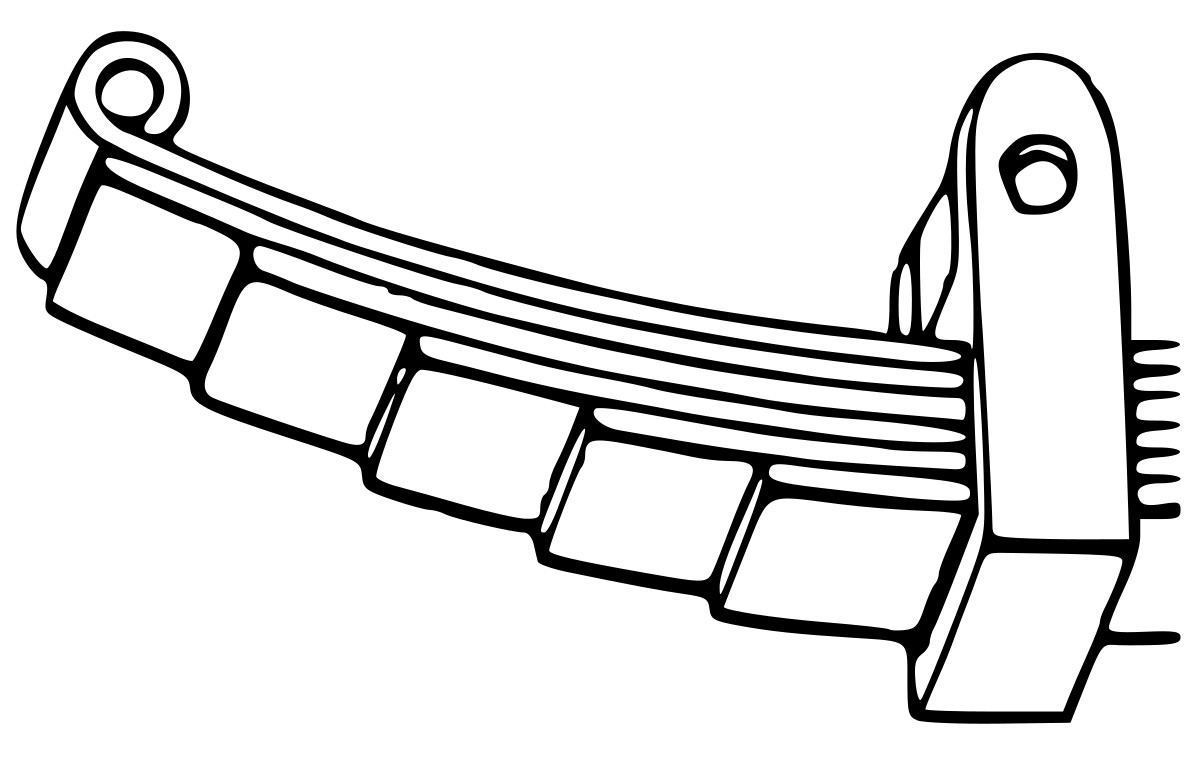
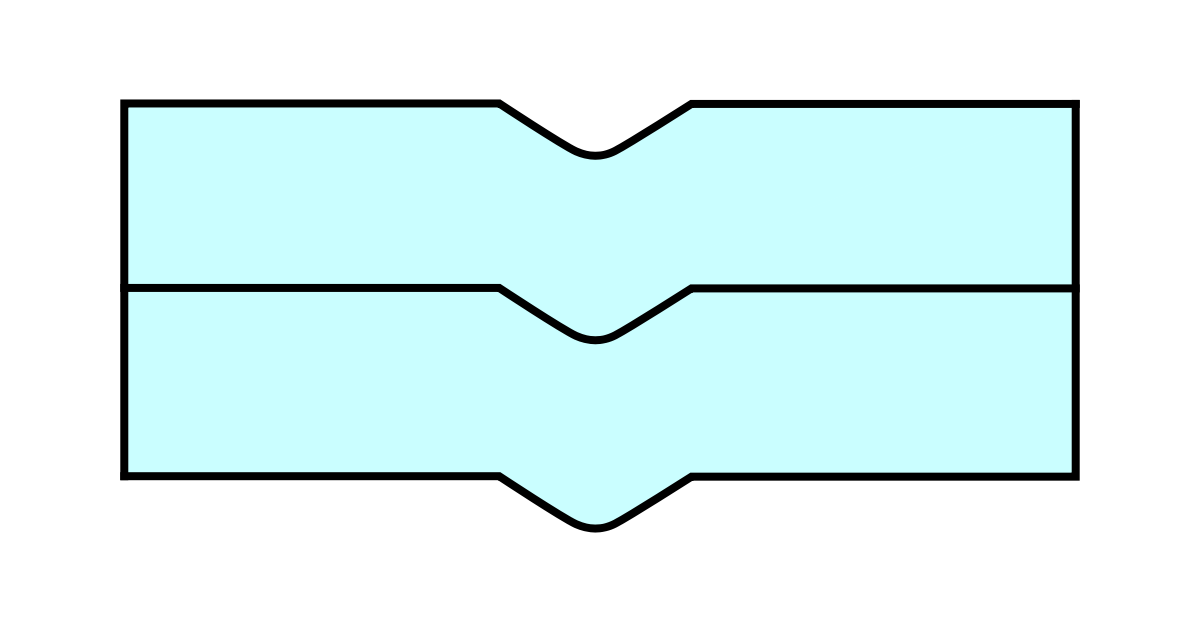
• les lames ne sont généralement pas de section rectangulaire, elles portent des nervures qui les maintiennent alignées, comme le montre la figure ci-après. Il existe d'ailleurs des profilés normalisés spécialement formés pour la réalisation de ressorts à lames.

• la nécessité de brider les lames au centre impose d'augmenter la longueur du ressort car la partie bridée se trouve raidie.

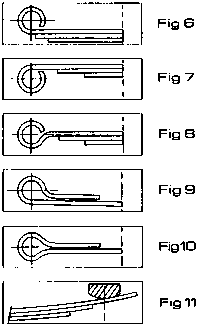
• les attaches peuvent prendre des formes très diverses dites à œil droit (6), renversé (7), épaulé (8), droit à patte (9), épaulé à patte (10), appui à glissoir (11).

Si l'on ajoute la possibilité de réaliser des ressorts à lames étagées de toutes formes, symétriques ou non, à faible ou forte courbure, etc., il devient évident que les formules théoriques établies au début de ce paragraphe doivent être pour le moins revues et corrigées. En fait, chaque ressort nécessite une étude individualisée.

Le frottement entre les lames produit des pertes d'énergie notables (le travail de déformation du ressort est loin d'être intégralement restitué au moment de la détente) mais ces pertes contribuent à l'amortissement des vibrations, par exemple dans le cas des ressorts de suspension. Cependant, outre le fait qu'il fausse un peu plus les formules, le frottement est capable d'engendrer le phénomène de corrosion-frottement (poudre rouge) très destructeur. Pour éviter ou au moins pour freiner cette forme particulière d'usure, une lubrification protectrice est absolument indispensable et il ne faut surtout pas que l'état de surface des lames soit trop bon. Au contraire, il faut utiliser les lames « brutes de laminage ».