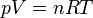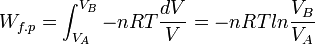Réversibilité et irréversibilité en thermodynamique - Définition

Phénomènes microscopiques et macroscopiques

Les problèmes résident dans l'approche microscopique ou particulaire de la mécanique classique où les objets étudiés sont des points matériels, ou bien des ensembles de points dont on oublie facilement la structure interne (comme pour le mouvement d'une planète dans le cosmos). A cette échelle et pour ce type d'objets étudiés individuellement, la physique semble réellement réversible. C'est la transition aux ensembles nombreux d'objets qui fait apparaitre le plus souvent les phénomènes irréversibles : c'est ce qu'on appelle le passage à la limite thermodynamique.

L'exemple le plus simple concerne les gaz. Alors qu'il est possible de déterminer un grand nombre de propriétés des gaz en considérant chaque particule comme ponctuelle et en utilisant exclusivement la mécanique classique, toutes les transformations des gaz sont irréversibles, et la plupart d'entre elles inexplicables sans la thermodynamique.

Les explications théoriques qui permettent de comprendre l'irréversibilité d'une transformation appliquée à une multitude d'objets microscopiques en évolution individuelle réversible sont fournies par la physique statistique et la théorie du chaos.

Exemples

Cycle compression-détente d'un gaz

Transfert thermique

Soit un corps solide de capacité thermique constante c, et de température initiale T. Son énergie interne est U(T) = c T et son entropie S(T) = c Ln T. Ce corps est mis en contact avec une source de température T' = x T. Sa température finale à l'équilibre sera donc T' et il aura échangé avec la source la chaleur Q = c (T'-T) = c T (x-1).

Étude de la variation d'entropie

On a, entre l'état initial et l'état final, la variation d'entropie suivante :

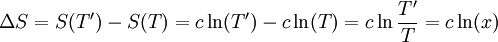
L'entropie échangée avec la source à la température T' est par définition :

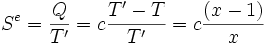
L'entropie créée S^c au cours de la transformation est donc, selon le second principe :

L'évolution est donc toujours irréversible, quelles que soient les températures finale et initiale.

Transformation quasi-statique

On imagine maintenant une transformation menant encore le corps solide de la même température initiale T à la même température finale T’ mais en mettant le corps successivement en contact avec une série de i sources de chaleur à des températures s'échelonnant graduellement de T à T'.

S étant une fonction d'état qui ne dépend que des conditions initiales et finales, la variation d'entropie reste inchangée :

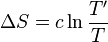
L'entropie échangée par le corps avec la source de chaleur i, à la température Tⁱ est égale à :

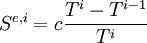
Si on considère que la transformation est réalisée de manière quasistatique, le nombre d'étapes, c'est-à-dire i, tend vers l'infini. Dans ce cas la différence de température (Tⁱ − T^{i − 1}) est infiniment petite et on pose dTⁱ = Tⁱ − T^{i − 1}.

L'entropie échangée totale par le corps est la somme des entropies échangées avec chacune des sources :

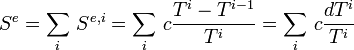
Pour i tendant vers l'infini et pour les température extrêmes T et T' on a :

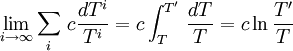
Et finalement, on trouve pour cette transformation quasi-statique une entropie créée limite :

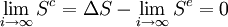
donc que la transformation tend à être réversible pour une transformation quasi-statique.

Expérience de Joule quasistatique

Interprétation microscopique

Frottement de Coulomb

Transformation réversible

Les conditions théoriques d'une transformation réversible sont les suivantes :

• continuité des grandeurs intensives,
• lenteur (transformations quasi-statiques),
• absence de phénomènes dissipatifs.

De manière plus précise on peut dire qu'une transformation réversible est un modèle idéal pour lequel les échanges de grandeurs extensives sont quasistatiques, réalisés en un grand nombre d'étapes pour que le déséquilibre des grandeurs intensives conjuguées soit réalisé par pas très faibles, et en l'absence de phénomènes dissipatifs. Il est très souvent possible, dans des conditions expérimentales adéquates, de se rapprocher de ce modèle.

Application au calcul du travail des forces de pression

Considérons la transformation isotherme réversible d’un gaz parfait partant d’un état initial A défini par les variables d'état : p(A), V(A), T, n pour aboutir à l’état final d’équilibre B défini par : p(B), V(B), T, n.

L’expression élémentaire du travail des forces de pression est : .

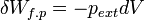
Si la transformation est réversible le déséquilibre entre la pression extérieure p_ext et la pression du gaz p est très faible pendant toute la transformation, donc p_ext ≈ p. De plus à chaque instant le système est à l’équilibre et peut être décrit par son Équation d'état. Si le gaz est parfait :

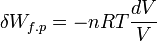
Le travail effectué au cours de la transformation correspond à l’intégrale définie pour une variation de volume entre V(A) et V(B) .

Ce calcul n’est possible que si la transformation est réversible. Le travail obtenu dépend ici de la façon de procéder à la transformation.