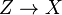Schéma intègre - Définition

Introduction

En mathématiques et plus particulièrement en géométrie algébrique, un schéma intègre est un schéma qui est localement défini par des anneaux intègres. Dans tout ce qui suit, le mot schéma peut être remplacé par variété algébrique sauf mention expresse du contraire.

Définition

Schémas réduits

On dit qu'un schéma X est réduit si pour tout ouvert U de X, l'anneau des fonctions régulières O_X(U) est réduit. Cela est équivalent à dire que les anneaux locaux O_X,x sont réduits pour tout point x. Ou encore qu'il existe un recouvrement de X par des ouverts affines SpecA_i avec A_i réduits.

Soit une fonction régulière sur X. On considère f comme une fonction de X vers un domaine universel qui contient tous les corps résiduels (à x on associé l'image de f par ). Si X est réduit, alors cette fonction est identiquement nulle si et seulement si f = 0.

Schémas intègres

On dit que X est intègre s'il est irréductible et réduit. C'est équivalent à dire que pour tout ouvert affine U = SpecA de X, l'anneau A est intègre. Lorsque X est localement noethérien, c'est encore équivalent à X connexe et que les anneaux locaux O_X,x sont intègres.

Sur un schéma intègre X, les anneaux de fonctions régulières O_X(U) sont intègres pour tout ouvert U, et les applications de restrictions sont injectives pour tout ouvert V contenu dans U.

Exemple Un schéma affine SpecA est intègre si et seulement si l'anneau A est intègre.

Différentes notions liées aux schémas intègres

Fonctions rationnelles

Soit X un schéma intègre. On pose

la limite inductive sur les O_X(U) de tous les ouverts non-vides U (les applications de transition sont les applications de restriction). Pour tout ouvert affine U non-vide, le morphisme canonique induit un isomorphisme de K(X) avec le corps des fractions Frac(O_X(U)). On appelle les éléments de K(X) les fonctions rationnelles (et parfois des fonctions méromorphes) sur X et K(X) le corps des fonctions rationnelles sur X.

Concrètement, une fonction rationnelle sur X est (la classe d') une fonction régulière f sur un ouvert dense U; deux fonctionns rationnelles (f,U),(g,V)étant considérées comme identique si f = g sur .

Étant donnée une fonction rationnelle f, l'ensemble des points x tel que f soit régulière dans un voisinage de x est le plus grand ouvert sur lequel f est régulière. Sur un schéma noethérien normal, le complémentaire de cet ouvert est vide ou de codimension 1, et c'est le support du diviseur de pôles de f.

On vient de voir que K(X) est isomorphe à Frac(O_X(U)) pour tout ouvert affine U. Si η est le point générique (ceci n'est pas valable pour les variétés algébriques) de X, alors K(X) est canoniquement isomorphe à l'anneau local O_X,η.

Si U est un ouvert dense de X, alors on a canoniquement K(X) = K(U).

Exemples

• Les corps des fonctions rationnelles sur Spec(k[T]) et Proj(k[T₀,T₁]) sont isomorphes à k(T).

• Si est un polynôme non-constant et qui n'est pas un carré, et si k est de caractéristique différente de 2, alors X = Spec(k[T,S] / (S² − f(T))) est intègre, son corps des fonctions rationnelles est l'extension quadratique k(T)[s] de k(T) définie par la relation s² = f(T).

Si X est de type fini sur un corps k, alors k(X) est une extension de type fini de k, de degré de transcendance dimX. C'est un corps de fonctions sur k.

Applications rationnelles

Soient X un schéma intègre et Y un schéma séparé. Deux morphismes , définis sur des ouverts denses de X sont dit équivalents s'ils coincident sur . Comme Y est séparé, il suffit qu'ils coincident sur un ouvert dense contenu dans . Cette relation est alors une relation d'équivalence.

Une application rationnelle de X dans Y, qu'on note (une flèche pointillée), est une classe d'équivalence de morphismes . Si un morphisme est dans la classe φ, on dit que φ est définie sur U. En prenant la réunion de tous les ouverts où φ est définie, on obtient le plus grand ouvert Ω où φ est définie: c'est le domaine de définition de φ.

Soit X un schéma intègre de type fini sur un corps k. Soit une fonction rationnelle et soit Ω le plus grand ouvert sur lequel f est régulière. On a un morphisme correspondant au morphisme de k-algèbres qui envoie T sur f. Comme Spec(k[T]) est un ouvert de la droite projective , on obtient canoniquement un morphisme . Sa classe d'équivalence est donc une application rationnelle

Si est un point rationnel, cette application rationnelle envoie x sur . Inversement toute application rationnelle provient d'une fonction rationnelle (considère le morphisme ).

Ainsi a-t-on une correspondance bi-univoque entre les fonctions rationnelles sur X et les applications rationnelles .

Morphismes dominants

Un morphisme entre schémas intèges est dominant si le sous-ensemble f(X) est dense dans Y. C'est équivalent à dire que le morphisme canonique de faisceaux est injectif. On en déduit immédiatement un morphisme des corps de fonctions rationnelles . C'est une extension de corps.

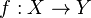
Dans le langage des schémas, f dominant se traduit par la propriété que f envoie le point générique de X sur celui de Y.

Exemples

• Tout morphisme surjectif est dominant. En particulier si le schéma d'arrivée Y est réduit à un point (i.e. est égal au spectre d'un corps), alors f est automatiquement dominant.
• Si dimY = 1, alors f est constant ou dominant.

Si est dominant et de type fini:

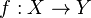
• l'extension K(X) / K(Y) est de type fini;
• on dit que est birationnel si l'extension k(X) / k(Y) est triviale (i.e. est un isomorphisme);
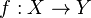
• si de plus X,Y sont de type fini sur un corps k et que f est un morphisme de k-schémas, alors K(X) / K(Y) est une extension de degré de transcendance dimX − dimY. En particulier, si dimX = dimY, alors K(X) / K(Y) est une extension finie;
• si f est projectif (par exemple si X,Y sont projectifs sur un schéma S et que f est un morphisme de S-schémas), alors il est surjectif puisque f(X) est fermé et dense dans Y.

Tout morphisme de schémas intègres se décompose en un morphisme dominant suivi d'une immersion fermée . Il suffit de prendre pour Z la partie fermée de Y munie de l'unique structure de sous-schéma fermé réduit (donc intègre puisqu'il est irréductible).

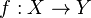
Si X,Y sont de type fini sur un schéma S et si est une application rationnelle associée à des S-morphismes , on dit que φ est une application birationnelle si est dominant et si l'extension des corps de fonctions K(X) = K(Ω) / K(Y) est triviale. Cela implique qu'il existe un ouvert dense tel que φ induise un isomorphisme de U sur un ouvert dense de Y. Deux schémas intègres de type fini sur S sont dits birationnels s'il existe une telle application birationnelle.

Résolution du lieu d'indéterminance

Il existe une façon canonique de rendre une application rationnelle définie partout.

Soit une application rationnelle dont le domaine de définition est Ω. Considérons le produit fibré (on peut remplacer par Spmk s'il s'agit de variétés algébriques sur k) muni de ses projections p,q sur X,Y. Considérons l'ensemble des points (x,φ(x)) avec dans ce produit, et son adhérence Z munie de la structure de sous-schéma fermé réduit. On obtient un schéma intègre Z, un morphisme birationnel , et un morphisme .

Ainsi, modulo le morphisme birationnel , l'application rationnelle φ devient un morphisme .