Similitude (géométrie) - Définition

Introduction

Dans ce dessin, les objets de même couleur sont semblables.

En géométrie euclidienne, une similitude est une transformation qui met en relation toute figure avec une figure semblable, de même forme. Par exemple, l’image d’un carré par une similitude est un carré. Et tout triangle rectangle isocèle est semblable à n’importe quel triangle rectangle isocèle. Si la similitude agit sur l’espace à trois dimensions, elle transforme un cube en un cube, et une sphère en une sphère. N’importe quelle figure géométrique est semblable à elle-même, car la transformation à l’identique est une similitude particulière. Et n’importe quel cercle est semblable à n’importe quel cercle. Une similitude transforme un triangle équilatéral en un triangle équilatéral. Une autre page est consacrée aux triangles semblables.

Rapports de longueurs, de superficies, ou de volumes

Le rapport k d’une similitude est le coefficient de proportionnalité entre les longueurs d’une première figure géométrique, et les longueurs correspondantes dans l’image de la première par la similitude. Autrement dit, la seconde figure reproduit la première à l’échelle k.  Le nombre  k × k  ou  k²  est alors le coefficient de proportionnalité entre les superficies correspondantes — au lieu de “superficie”, on dit aussi “aire” —. Et k³ est le coefficient de proportionnalité entre les volumes correspondants, quand la similitude est définie dans l’espace à trois dimensions.

Par exemple, une similitude de rapport dix multiplie les longueurs par dix et les aires par cent. Si une similitude de rapport dix est définie dans l’espace à trois dimensions, elle multiplie les volumes par mille. Si une similitude de l’espace multiplie les volumes par deux, alors son rapport est le nombre positif k tel que k³ = 2.  Ce nombre k est la racine cubique de 2, qui peut s’écrire 2^1/3.

Les similitudes de rapport 1 sont des isométries. Par exemple, les rotations, les translations et les symétries sont des similitudes de rapport 1.

Les homothéties sont des similitudes, et il faut noter l’ambiguïté du mot rapport. Le rapport d’une homothétie concerne des vecteurs, il peut être négatif, tandis que le rapport d’une similitude est un rapport de distances, toujours positif. Par exemple, une homothétie de rapport négatif -1 est une symétrie par rapport à son centre, ou une similitude de rapport positif 1, et d’angle 180° (un demi-tour). Dans tous les cas, une homothétie de rapport k est une similitude de rapport positif |k|.

Exemple avec racine carrée de deux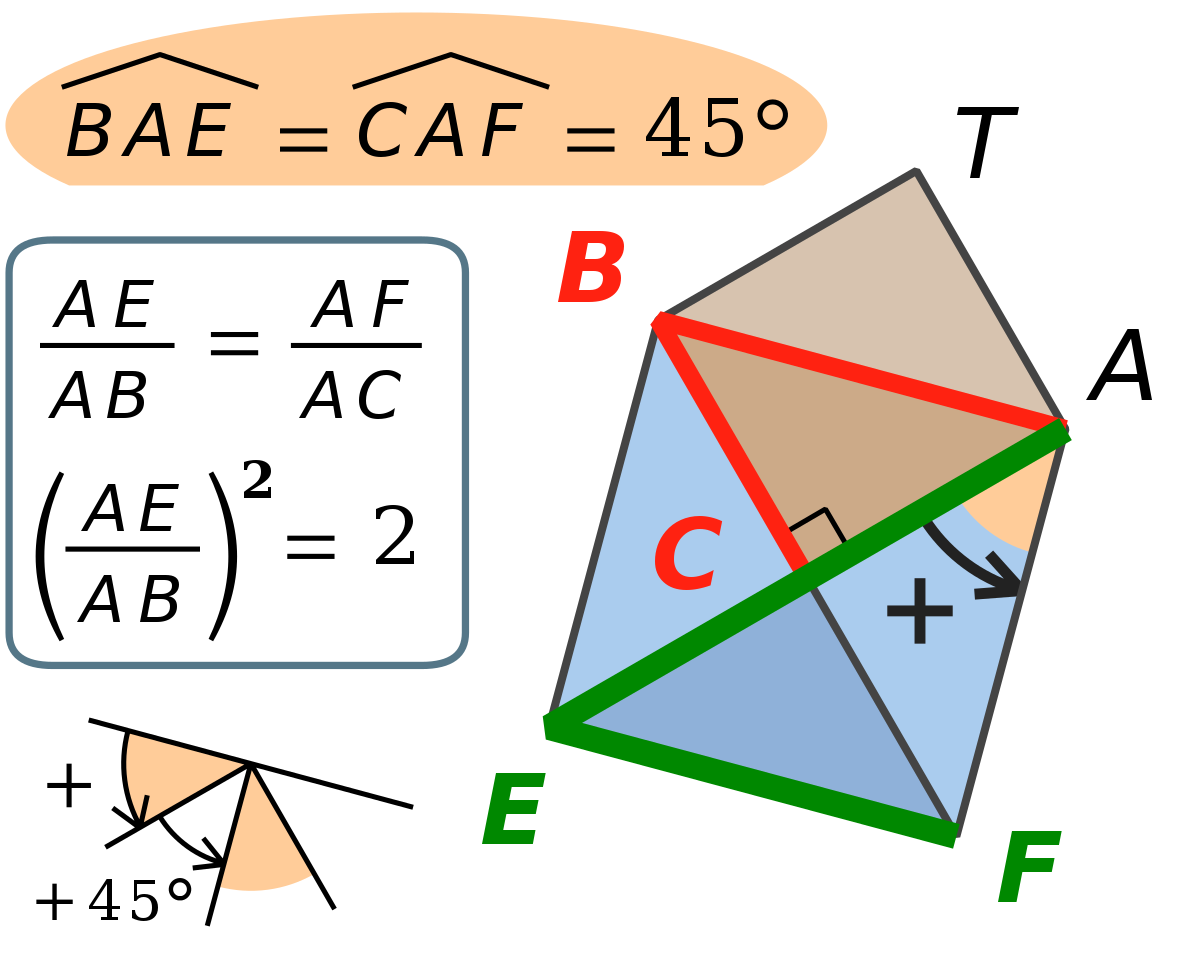 Le triangle EFC reproduit le triangle ABC à l’échelle √2, parce que son aire est deux fois celle de ABC. Pour trouver le rapport des longueurs d’une diagonale à un côté d’un carré, il suffit d’exprimer l’aire d’un triangle rectangle isocèle, soit en fonction de la longueur des côtés de l’angle droit, soit en fonction de la hauteur relative à l’hypoténuse. Dans la figure à droite, ABTC et EFBC sont deux carrés, et EFC est un triangle rectangle isocèle. Le double de son aire soit  EF × EC,  qui peut s’écrire  EC2,  soit  FC × AE.  Or, FC est le double de AC. Donc, l’aire de EFC est égale à  AC × AE,  ou  AC2.  Conclusion :  EC2 = 2 × AC2,  dont on déduit   (EC/AC)2 = 2. Une similitude de centre C et d’angle 45° (angle orienté positif, quand on tourne dans le sens trigonométrique, ou anti-horaire) transforme le carré ABTC en EFBC, et le triangle rectangle isocèle ABC en EFC. Les deux côtés de ABC tracés en rouge deviennent les deux côtés de EFC tracés en vert. Le triangle ABC est numéroté 1, les triangles qui pavent EFC sont numérotés 1 et 2, ils sont isométriques à ABC — superposables à ABC —. Le rapport de l’aire de EFC à l’aire de ABC est 2/1, ou 2. Le rapport de la similitude est donc le nombre positif dont le carré est 2,  autrement dit :  EC/AC = EF/AB = FC/BC = √2 = 21/2.  Ce nombre est l’inverse de cos(45°). Dans l’égalité  √2 × √2 = 2,  le signe × a attendu des siècles avant d’avoir une signification rigoureuse. Aucune fraction n’est égale à √2, ce fut prouvé dès l’Antiquité. Les multiplications ne portaient alors que sur des entiers ou des fractions. De nos jours, l’égalité est absolument exacte en théorie des nombres “réels”. Le nombre √2 ainsi que son produit par lui-même sont maintenant rigoureusement définis, dans la théorie des suites de Cauchy, ou bien dans la théorie des coupures de Dedekind.

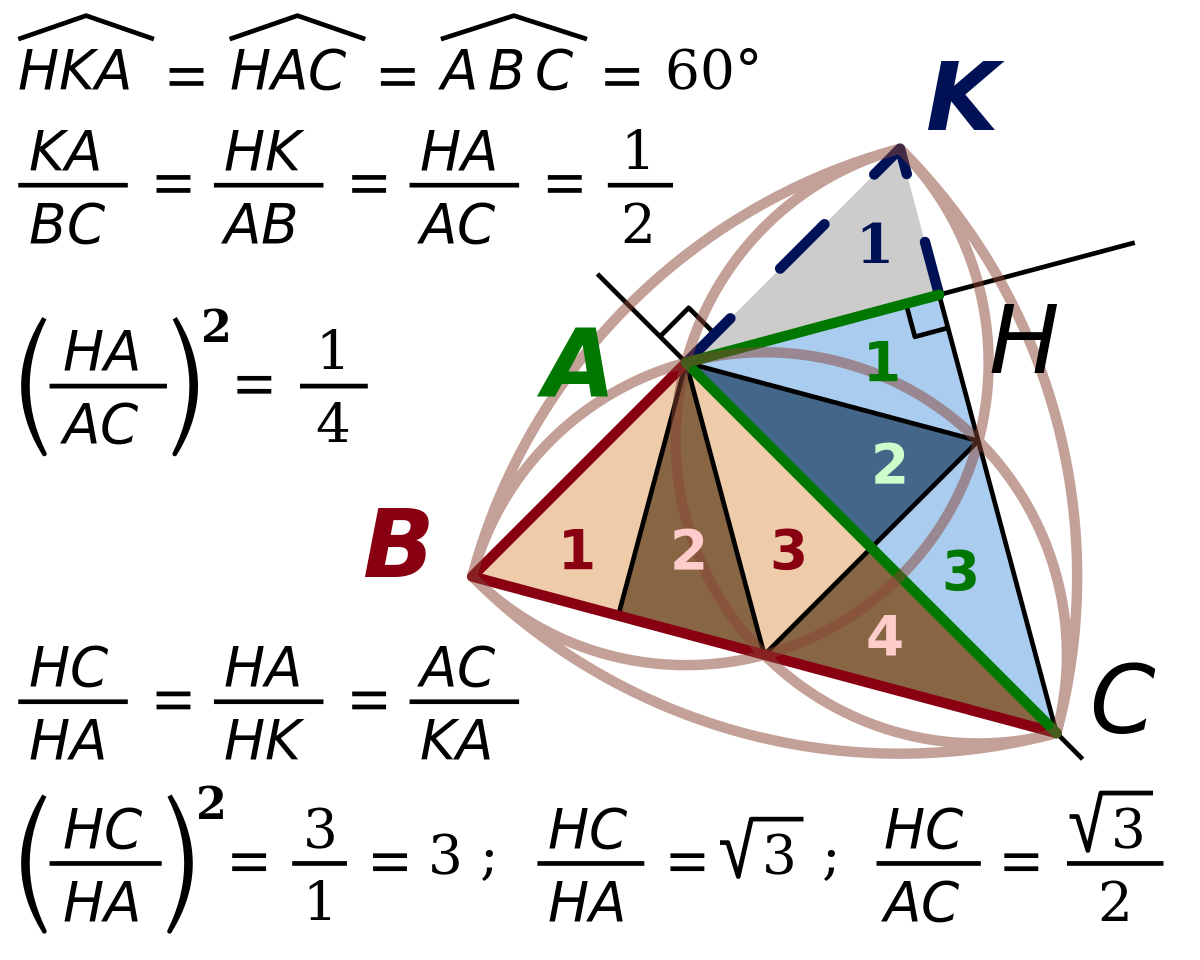
Avec tan(60°) et sin(60°) Le triangle HAC reproduit le triangle ABC à l’échelle √3/4, parce que l’aire de HAC est égale aux trois quarts de l’aire de ABC. Le triangle BCK est équilatéral. Le point H est le projeté orthogonal sur (KC) du milieu A de [BK]. Huit triangles rectangles tous isométriques entre eux constituent un pavage de BCK, quatre de part et d’autre de la médiatrice de [BK]. L’un des triangles du pavage est HKA. Une similitude de rapport 1/2 et d’angle négatif -120° transforme ABC en HKA en divisant par 4 son aire :  cos(60°) = HA/AC = HK/AB = KA/BC = 1 / 2,   et  (HA/AC)2 = 1/4.  Une similitude de centre H et d’angle +90° transforme HKA en HAC en multipliant son aire par trois. Le rapport de cette similitude est :  tan(60°) = HC/HA = HA/HK = AC/KA = √3.  La composée des deux similitudes est la similitude de centre C, d’angle -30°, et de rapport sin(60°). Elle transforme deux côtés de ABC tracés en rouge en deux côtés de HAC tracés en vert. Les deux côtés correspondants de HKA sont en pointillé bleu. Ainsi les valeurs de tan(60°) et sin(60°) sont mises en évidence :  sin(60°) = tan(60°) / 2 = √3 / 2.

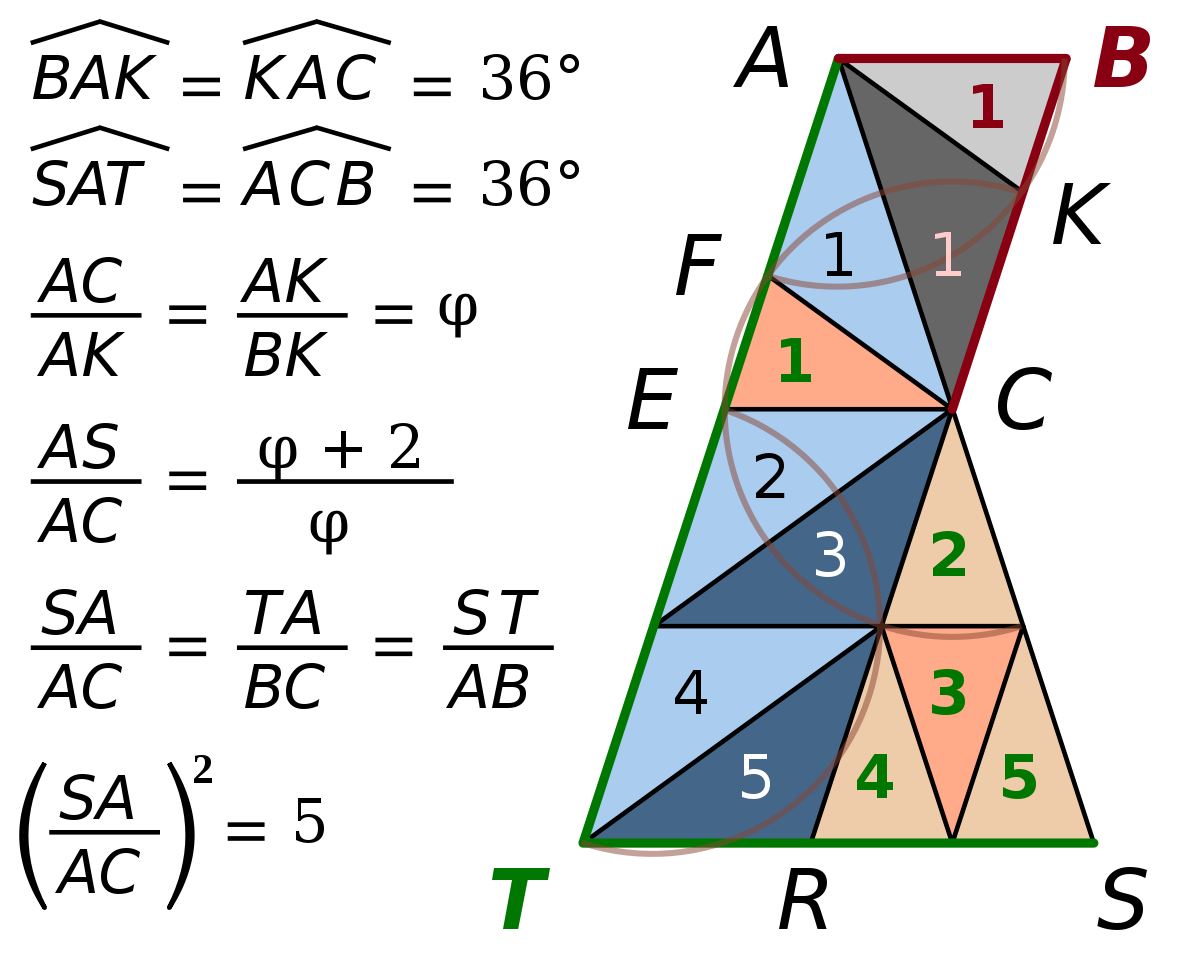
Avec racine carrée de cinq Le triangle STA reproduit le triangle ABC à l’échelle √5, parce que son aire est cinq fois celle de ABC. Le pentagone ABCST est pavé de douze triangles isocèles de deux sortes différentes. Deux d’entre eux pavent ABC, un de chaque sorte : BKA et AKC. Les dix autres triangles du pavage remplissent STA, cinq de chaque sorte. Cinq d’une sorte sont isométriques à AKC, ils ont deux angles égaux à 36°. Les cinq autres sont isométriques à BKA, ils ont deux angles égaux à 72°. Ainsi, l’aire de STA est cinq fois celle de ABC. Une similitude de rapport √5 et d’angle 180° transforme ABC en STA. Elle transforme les deux côtés de ABC tracés en rouge en deux côtés de STA tracés en vert. Les rapports de longueurs  AC/AK  ou  AK/BK  sont égaux à φ, le nombre d’or :  2.cos(36°) = 1/(2.cos(72°)) = φ.  Le rapport de la précédente similitude peut donc s’écrire :  √5 = TA/BC = ST/AB = (φ + 2) / φ. On en déduit cette valeur du nombre d’or :  φ = (1 + √5) / 2.