Solide de Kepler-Poinsot - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
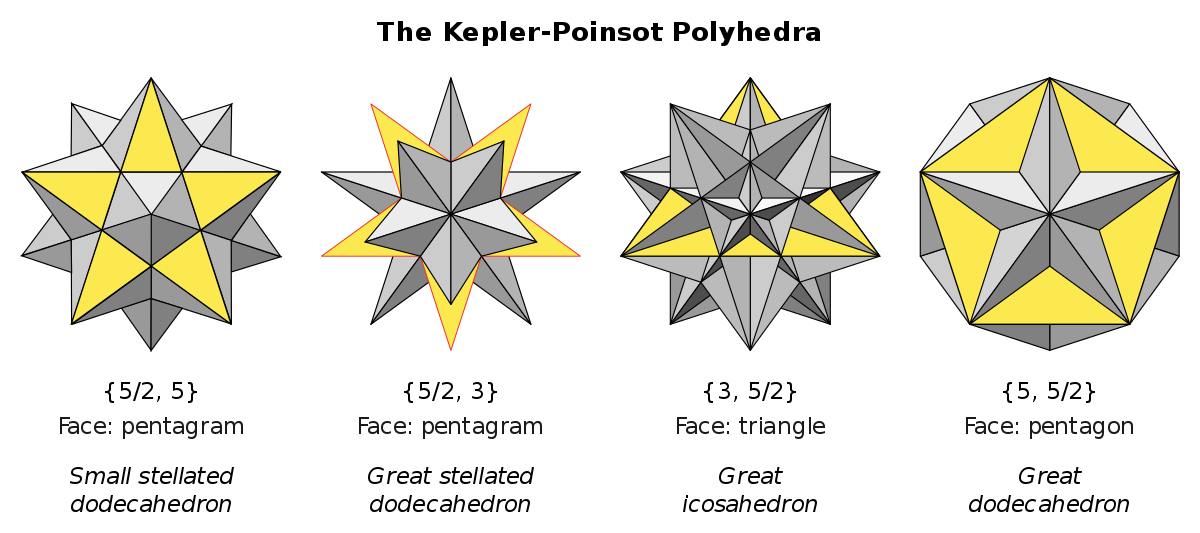
Les solides de Kepler-Poinsot sont les polyèdres étoilés réguliers. Chacun possède des faces qui sont des polygones convexes réguliers congruents ou des polygones étoilés et possède le même nombre de faces se rencontrant à chaque sommet (comparer avec les solides de Platon).
Il existe quatre solides de Kepler-Poinsot :
- le petit dodécaèdre étoilé
- le grand dodécaèdre étoilé
- le grand dodécaèdre
- le grand icosaèdre.
Géométrie
| Nom | Image | Symbole de Schläfli {p,q} | Faces {p} | Arêtes | Sommets {q} figsom. | χ | Symétrie | Dual |
|---|---|---|---|---|---|---|---|---|
| Petit dodécaèdre étoilé |

| {5/2,5} | 12 {5/2} | 30 | 12 {5} | -6 | Ih | Grand dodécaèdre |
| Grand dodécaèdre étoilé |

| {5/2,3} | 12 {5/2} | 30 | 20 {3} | 2 | Ih | Grand icosaèdre |
| Grand dodécaèdre |

| {5,5/2} | 12 {5} | 30 | 12 {5/2} | -6 | Ih | Petit dodécaèdre étoilé |
| Grand icosaèdre |

| {3,5/2} | 20 {3} | 30 | 12 {5/2} | 2 | Ih | Grand dodécaèdre étoilé |
Le petit et le grand dodécaèdre étoilé ont des faces en forme de pentagrammes non convexes réguliers. Le grand dodécaèdre et le grand icosaèdre ont des faces en forme de pentagones convexes, mais ont des figures de sommets en forme de pentagrammes. La première paire et la deuxième sont les duaux les uns les autres.
Ces figures peuvent induire en erreur, car elles incluent les pentagrammes comme des faces et des figures de sommets. Les faces et les sommets peuvent être supposés de manière erronée où les faces se coupent, mais ils ne sont pas comptés.
Si les intersections sont comptées comme de nouvelles arêtes et de nouveaux sommets, ils ne seront pas réguliers, mais ils peuvent encore être considérés dans les stellations. (voir aussi la Liste des modèles de polyèdres de Wenninger)
La caractéristique d'Euler
Un solide de Kepler-Poinsot couvre sa sphère circonscrite plus d'une fois. A cause de cela, ils ne sont pas nécessairement topologiquement équivalent à la sphère comme le sont les solides de Platon, et en particulier, la caractéristique d'Euler
- S - A + F = 2
n'est pas toujours valide.
La valeur de la caractéristique d'Euler χ dépend de la forme du polyèdre. Considérons par exemple le petit dodécaèdre étoilé [2]. Il est constitué d'un dodécaèdre avec une pyramide pentagonale sur chacune de ses douze faces. Chacune des douze faces est un pentagramme avec la partie pentagonale cachée dans le solide. La partie extérieure de chaque face est constituée de cinq triangles qui se touchent seulement en cinq points. Alternativement, nous pourrions compter ces triangles comme des faces séparées - il y en 60 (mais ils sont seulement des triangles isocèles, et non des polygones réguliers). De manière similaire, chaque arête serait maintenant divisée en trois arêtes (mais alors, ils sont de deux sortes). Les "cinq points" que l'on vient de mentionner, forment ensemble les 20 sommets supplémentaires, ainsi, nous avons un total de 32 sommets (de sortes, de nouveau). Les pentagones internes cachés ne sont pas nécessaires pour former la surface du polyèdre et peuvent disparaitre. Maintenant, la relation d'Euler est valable : 60 - 90 + 32 = 2. Néanmoins, ce polyèdre n'est pas celui décrit par le symbole de Schläfli {5/2,5}, et donc, ne peut pas être un solide de Kepler-Poinsot même s'il y ressemble encore d'aspect extérieur.