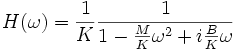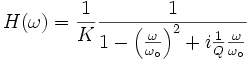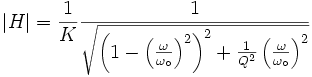Système oscillant à un degré de liberté - Définition

Facteur de qualité et oscillations forcées

Dans le même exemple précédent on peut écrire la fonction de transfert comme:

mais et .

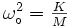
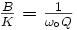
Avec ceci, la fonction de transfert peut s'écrire:

Le module de la fonction de transfert est:

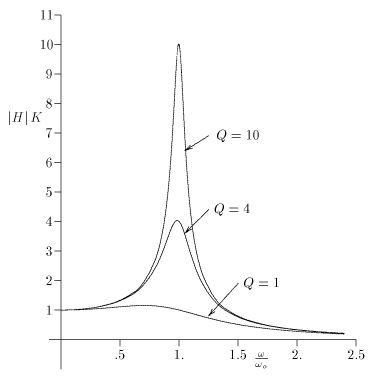
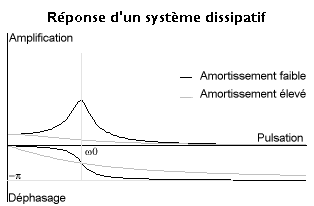
En observant les courbes de droite on comprend mieux l'intérêt d'utiliser le facteur de qualité Q. L'amplitude à la résonance ( ) est Q fois l'amplitude en basse fréquence.

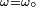
Oscillations forcées

Généralités

Ces oscillations correspondent à une équation non homogène qui s'écrit

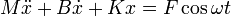
Selon la théorie, la solution générale d'une telle équation est égale à la somme de la solution générale de l'équation homogène et d'une solution particulière de l'équation non homogène. Ceci se traduit en disant que le mouvement obtenu est la somme de l'oscillation propre, qui dépend des conditions initiales, et de l'oscillation forcée par la force extérieure ; on parle aussi de réponse à l'excitation décrite par le second membre. Généralement, il suffit de ne considérer que cette réponse qui subsiste seule après l'extinction de l'oscillation propre due à l'amortissement.

Pour ce faire il est commode d'utiliser les nombres complexes en considérant simultanément l'équation

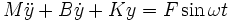
et d'ajouter cette équation multipliée par i à la précédente. En posant x + i y = z, on obtient

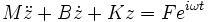
La recherche d'une solution z = Ze^iωt conduit à

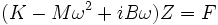
En ignorant pour l'instant la forme exacte, cette équation se réécrit

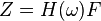
H(ω) représente la fonction de transfert qui décrit la réponse en fonction de la pulsation. Elle peut s'exprimer en module et argument :

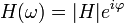
d'où

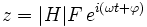
La partie réelle est

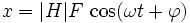
Ainsi, à une excitation sinusoïdale un système linéaire fait correspondre une réponse sinusoïdale de même pulsation. De même, à une somme de sinusoïdes correspond une somme de sinusoïdes. Pour chacune d'entre elles le module et l'argument de la fonction de transfert représentent respectivement l'amplification et le déphasage. A l'inverse, toute non-linéarité crée des composantes qui n'existent pas dans l'excitation.

Systèmes conservatifs

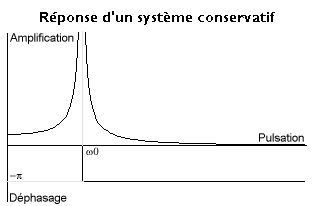
La fonction de transfert s'écrit

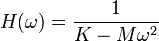
Son module est

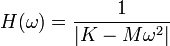
L'amplification croît avec un déphasage nul à partir de la valeur statique F/K jusqu'à l'infini lorsque ω atteint la valeur ω₀. Ensuite elle décroît jusqu'à zéro avec un déphasage égal à -π.

La valeur infinie correspond à la résonance lorsque le système est excité à sa pulsation propre. Dans la conception d'un système, le simple calcul de cette pulsation (ou fréquence ou période propre) peut conduire à modifier l'inertie ou la raideur d'un système pour l'éloigner des excitations attendues. En tout état de cause, la réponse ne peut être que finie à cause de l'amortissement qui est négligé ici.

Systèmes dissipatifs

Dans ce système plus réaliste, la fonction de transfert devient

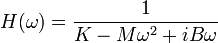
L'amplification est

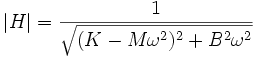
Il apparaît que le dénominateur de la fonction de transfert ne peut plus s'annuler : pour un amortissement faible on a une courbe de réponse voisine de celle du système non amorti mais avec un maximum fini. En annulant la dérivée de |H| par rapport à ω², on obtient la pulsation qui donne ce maximum :

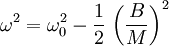
A mesure que le coefficient d'amortissement B augmente, l'abscisse du maximum diminue jusqu'à 0 où la fonction de ω devient décroissante, ce qui se produit pour l'amortissement critique

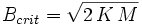
Le déphasage est défini par

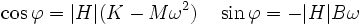
Pour les plus petites valeurs de la pulsation on a le régime quasi-statique dominé par la raideur dans lequel la réponse est en phase avec l'excitation ; pour les plus grandes, on atteint le régime dominé par l'inertie dans lequel la réponse est en opposition et l'amplification est de l'ordre de F/Mω². L'amortissement devient essentiel loin de ces deux extrêmes.