Système oscillant à un degré de liberté - Définition

Introduction

Les phénomènes physiques dépendant du temps sont généralement décrits au départ par des équations différentielles. Dans le cas le plus simple, il y a une seule grandeur qui varie et on parle de système à un degré de liberté, la plupart du temps régi par une équation différentielle du second ordre. Les phénomènes naturels sont presque toujours non-linéaires mais, dans de nombreux cas, l'hypothèse des petits mouvements permet d'aboutir à une excellente approximation fournie par une équation différentielle linéaire à coefficients constants d'ordre deux. Cet article a pour but de donner une interprétation physique de la théorie correspondante.

Généralités

Système masse-ressort

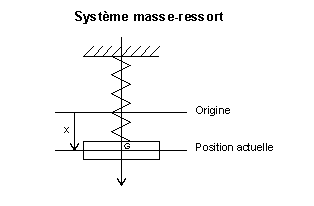
En mécanique, cette équation concerne particulièrement le système masse-ressort constitué par une masse accrochée à un ressort et contrainte de se déplacer dans une seule direction. Son mouvement est dû à trois forces :

• une force de rappel F_R,
• une force d'amortissement F_A,
• une force extérieure F_E.

M étant la masse et x sa position comptée à partir de l'équilibre, l'équation du mouvement s'écrit alors

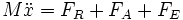
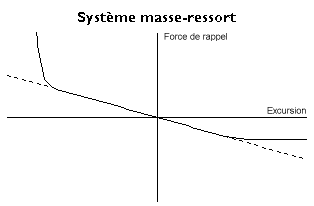
La force de rappel est une fonction de la position qui varie en sens inverse de l'excursion, tout en passant par l'origine lorsque les excursions sont comptées à partir du point d'équilibre. Si on suppose qu'elle est fournie par un ressort hélicoïdal, au delà d'une certaine extension le ressort se détend et l'allongement varie beaucoup plus vite que la tension. Inversement, au delà d'une certaine compression les spires deviennent jointives et il faut fournir des efforts considérables pour faire varier la longueur. En se plaçant dans le cas des petits mouvements, la fonction compliquée ainsi obtenue se réduit à une fonction linéaire dans laquelle K est la raideur du système (Loi de Hooke) :

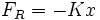
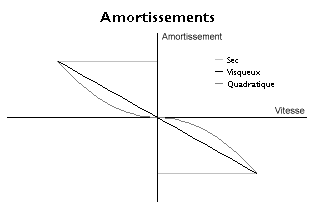
En ce qui concerne l'amortissement, qui dépend de la vitesse, on peut rencontrer un amortissement quadratique produit par les tourbillons ou la turbulence dans un fluide ou un frottement sec entre deux solides, à peu près indépendant de la vitesse. Néanmoins, à l'aide d'un raisonnement analogue au précédent, on est souvent amené à considérer un amortissement linéaire. Celui-ci s'observe en particulier dans un fluide, lorsque la vitesse est suffisamment faible pour que la viscosité ne soit plus négligeable (voir Nombre de Reynolds). On a alors, B étant le coefficient d'amortissement :

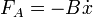
Enfin, la force extérieure peut être représentée par n'importe quelle fonction du temps f(t), ce qui conduit à l'équation

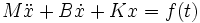
Systèmes analogues

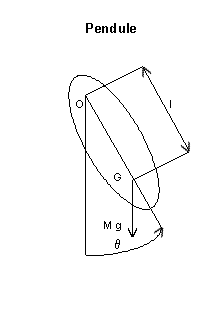
On trouve une équation analogue dans d'autres problèmes de mécanique comme celui du pendule décrit par sa masse M, son moment d'inertie I, un coefficient d'amortissement B, la distance l de son centre de gravité à l'axe de rotation et un moment excitateur m(t). Si θ représente l'excursion angulaire, l'équation du mouvement s'écrit

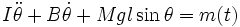
Si on s'en tient aux petits mouvements, l'équation se réduit à

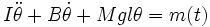
Cette équation est identique à celle du système masse-ressort.

En électricité on trouve aussi une équation du même type pour un circuit comportant une auto-inductance L, une résistance R, une capacité C. La quantité d'électricité q engendrée par une tension v(t) est donnée par

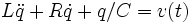
Problèmes particuliers considérés

Dans les équations ci-dessus, les coefficients sont tous positifs, ce qui, comme on le verra plus loin, assure la stabilité du système sans laquelle il serait sans grand intérêt d'exprimer les solutions en détail.

En ce qui concerne la force excitatrice du second membre on est amené à considérer deux types de problèmes. Si ce second membre est nul, il s'agit d'oscillations libres obtenues en écartant le système de sa position d'équilibre.

A l'opposé, une excitation non nulle crée des oscillations forcées qui subsistent seules après l'extinction des oscillations libres due à l'amortissement. Le problème de base concerne l'excitation sinusoïdale. Celui-ci est non seulement intéressant en lui-même mais la linéarité du système permet aussi, grâce au techniques d'analyse spectrale, d'étendre les résultats obtenus à des excitations beaucoup plus compliquées considérées comme des sommes de sinusoïdes.

Enfin, bien que le mouvement perpétuel ne puisse exister, toute oscillation non entretenue s'éteignant plus ou moins rapidement, il est commode dans certaines circonstances de négliger l'amortissement et de distinguer les systèmes conservatifs des systèmes dissipatifs.