Système oscillant à un degré de liberté - Définition

Q ou facteur de qualité

Pour décrire l'amortissement d'un système oscillant mécanique ou électrique on emploie le facteur de qualité ou simplement le Q du système. Dans le système mécanique précèdent, il est défini comme:

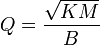
Un système très amorti a un Q faible. À l'inverse, un Q élevé correspond à un système peu amorti. Pour fixer les idées, le Q d'une voiture avec des amortisseurs en bon état est légèrement supérieur à 1. Le Q d'une corde de guitare est de quelques milliers. Celui des quartz utilisés en électronique pour fabriquer des oscillateurs stables est de l'ordre de quelques millions.

Avec les notations précédentes, il vient β = 1 / 2Q. En introduisant le nombre d'oscillations n(t) = ω₀t / 2π, l'oscillation s'écrit pour β<1

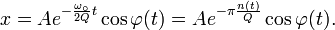
Ainsi, pour des oscillateurs peu amortis, le Q est égal à π fois le nombre d'oscillations que le système fait pendant que son amplitude tombe d'un facteur 1/e ou à 3 fois le nombre d'oscillations pour que l'amplitude tombe à 1/3 si l'on tolère une approximation plus grossière.

Puisque l'énergie mécanique de l'oscillateur est proportionnelle au carré de l'amplitude, Q est aussi égal à 2π fois le nombre d'oscillations effectuées avant que son énergie ne tombe d'un facteur 1/e, ce qui revient à dire que Q est aussi égal au nombre d'oscillations effectuées avant que son énergie ne tombe d'un facteur 1/e^2π≈1/535.

Oscillations libres

Systèmes conservatifs

Solution mathématique

L'équation d'un système sans amortissement écarté de sa position d'équilibre s'écrit donc

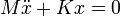
Selon la méthode décrite dans l'article précité sur les équations du second ordre, on cherche une solution de la forme x = e^rt, ce qui conduit à l'équation caractéristique

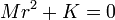
Cette équation possède deux racines imaginaires conjuguées. On peut remarquer au passage que, si la «raideur» K était négative, on obtiendrait deux racines réelles de signes opposés, la valeur positive entraînant une instabilité du système.

La solution générale s'écrit

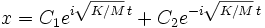
En utilisant les formules d'Euler, cette équation devient

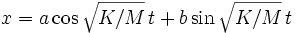
Solution en termes physiques

En posant a = A cos φ et b = -A sin φ, on obtient

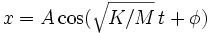
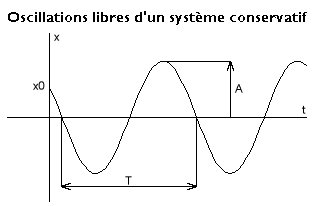
Le mouvement est représenté par une sinusoïde définie par une amplitude A, une phase φ et une pulsation exprimée en radians par seconde, dite pulsation propre, qui ne dépend que de la masse et la raideur du système :

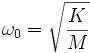
On en déduit la fréquence propre, nombre d'oscillations par seconde exprimé en hertz (Hz) :

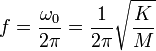
et la période propre, durée en secondes d'une oscillation :

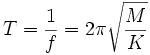
L'une ou l'autre de ces trois grandeurs constitue l'information essentielle sur le système. Il est bon de remarquer que, quel que soit ce système, une augmentation de la masse accroît la période tandis qu'une augmentation de la raideur accroît la fréquence.

Solution en fonction des conditions initiales

Les deux autres constantes peuvent s'interpréter en fonction de la position x₀ et la vitesse v₀ initiales. D'une manière générale, elles peuvent être prises en compte en utilisant la transformation de Laplace mais, dans ce cas précis, le calcul direct à partir de la première expression réelle est plus simple. On obtient :

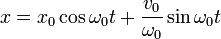
Solution en termes énergétiques

D'un point de vue énergétique, on calcule le travail des deux forces d'inertie et de rappel entre l'instant 0 et l'instant t par des formules du type

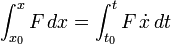
En faisant passer au second membre les termes constants, on obtient

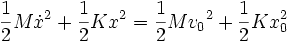
L'énergie totale du système, somme de l'énergie cinétique et de l'énergie potentielle, reste constamment égale à celle qui lui a été fournie en l'écartant de sa position d'équilibre. On parle de système conservatif qui n'existe pas dans la réalité car, dans tous les cas, l'énergie se dissipe à travers des phénomènes variés : il ne peut y avoir de mouvement perpétuel.

Systèmes dissipatifs

Solution mathématique

Dans un système réel, l'équation différentielle devient

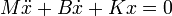
et son équation caractéristique

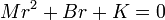
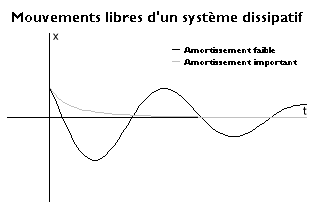
Il y a maintenant deux racines réelles ou complexes selon le signe du discriminant B² - 4 K M. Dans les deux cas, elles ont une partie réelle négative, ce qui fait tendre la fonction vers 0.

Si le coefficient d'amortissement B reste faible on a, par continuité avec le cas précédent, deux racines complexes conjuguées qui conduisent à une solution oscillante mais amortie. Les amortissements élevés qui rendent le discriminant positif interdisent toute oscillation.

Solution en termes physiques

Les formules se simplifient en utilisant la pulsation propre ω₀ du système non amorti et le paramètre β défini par 2 β ω₀ = B / M. Pour β < 1, il vient

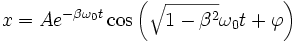
La pseudo-période de cette sinusoïde amortie est d'autant plus longue que l'amortissement est plus élevé. Lorsque β devient supérieur à 1, elle cesse d'exister et l'on a la solution

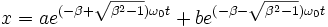
Solution en termes énergétiques

Le terme d'amortissement ne peut être intégré a priori. En le faisant passer dans le second membre, on obtient

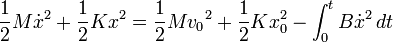
L'énergie totale du système diminuant constamment, le nouveau terme s'appelle fonction de dissipation. On peut remarquer qu'un « amortissement » négatif créerait de l'énergie.