Temps newtonien - Définition

Temps dynamique

Le temps dynamique absolu, dit souvent newtonien, est celui introduit par Newton dans les Principia (1687) : il permet de définir le temps, à une origine près, et à une unité près (la seconde, le jour, le siècle , ...). Ce temps est universel ; c'est une grandeur mesurable par toute horloge fonctionnant selon la définition suivante :

Le temps absolu est le paramètre réel qui intervient dans la loi (dite n°2) de Newton, appelée souvent PFD (Principe Fondamental de la Dynamique) du point matériel :

, avec

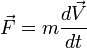
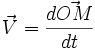
où F est une "bonne description" de l'action du milieu extérieur sur la particule ponctuelle M, de masse m (réel positif).

Alors la résolution de cette équation différentielle d'ordre deux donne le mouvement de M, et donc la donnée de l'abscisse curviligne s = s(t). D'où la fonction réciproque t = t(s), qui définit l'horloge de ce problème, via la mesure précise de l'abscisse s.

Newton a dit que cette loi est universelle et donc toutes les horloges fonctionnant sur ce principe indiquent le même temps : le temps dynamique absolu.

Le temps atomique

On sait construire depuis l'avènement des masers et des lasers en 1960, des oscillateurs ultra-stables, pilotés par l'oscillation d'une molécule. Ces horloges ont une précision bien plus grande que celle de l'horloge "Terre en révolution", d'où le choix de ces horloges pour définir l'unité de temps en 1967.

Cependant, la rotation de la Terre ralentit légèrement et comme par commodité anthropomorphique on veut que minuit reste au milieu de la nuit, on recale le temps universel coordonné, dérivé du temps atomique international, par une seconde intercalaire quand il le faut. Le temps universel coordonné ou UTC a remplacé l'ancienne référence, maintenant historique, du Greenwich Meridian Time ou GMT'

Exemple  : mouvement à force centrale

Tout mouvement à force centrale satisfait la deuxième loi de Kepler:

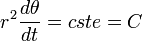
L'aire balayée est donc une excellente horloge absolue, cependant la difficulté pratique est de mesurer r(t) à chaque instant.

La Terre orbite autour du Soleil en un an selon une ellipse de Kepler : le paramètre aisément mesurable est l'angle polaire. Celui-ci varie selon une équation compliquée, dite équation du temps de Kepler, mais dont on sait évaluer numériquement la fonction réciproque avec la précision que l'on veut. Après chaque passage à l'équinoxe, le mouvement se répète à l'identique, d'après le calcul de Newton de 1684.

En réalité, ce n'est pas tout à fait vrai, car il faut entre autres tenir compte de l'influence non négligeable de la Lune, du soleil et de toutes les planètes, en particulier Jupiter. En définitive on connaît cet angle avec une précision relative de 10^-11.

On peut construire ainsi des éphémérides pour le mouvement de différents corps célestes, tous les temps donnés par ces différentes horloges coïncident. Il s'agit du principe retenu pour définir le temps des éphémérides.

Changement non affine de l'échelle de temps

Il est par contre plus subtil d'examiner comment se transforment les lois de Newton en choisissant un paramètre temps qui n'est pas un temps non absolu, mais qui reste une échelle de temps. Réciproquement, on peut se demander comment déterminer précisément, par l'observation, que le déroulement du temps est bien "absolu" : cette question est exactement le pendant, du point de vue temporel, de la question de savoir si un référentiel est bien galiléen ; par exemple, on n'a pu savoir que la Terre ne tournait pas "rond" (sous-entendu : le paramètre succession jour-nuit n'est pas un temps absolu) que parce que cette question a pu être tranchée.