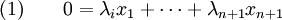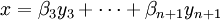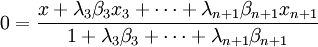Théorème de Carathéodory (géométrie) - Définition

Préparons d'abord le terrain pour la preuve en envisageant la situation suivante : soit un n + 1-uplet de ayant pour enveloppe affine tout entier, et positionné de telle sorte que . Pour chaque indice i entre 1 et n + 1, notons C_i l'ensemble des points x de qui peuvent s'écrire avec des coordonnées α_k toutes strictement positives (et pas de terme en y_i).

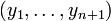
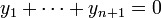
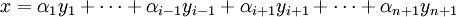
On vérifie alors aisément les informations suivantes :

• (i) Chaque C_i est un ouvert de
• (ii) Tout point de peut s'écrire de façon unique comme une combinaison linéaire à coefficients positifs ou nuls, l'un au moins des coefficients étant nul
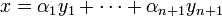
• (iii) Pour , C_i et C_j sont disjoints.

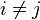
(Pour la première, on songera que est une base de et qu'on peut donc écrire tout point proche d'un de C_i par une formule ayant la même forme dans laquelle les coefficients sont proches des α_i ; pour la seconde, on s'assurera d'abord qu'étant donnée une écriture d'un point de Rⁿ comme combinaison linéaire des y_i, ses autres écritures comme telles combinaisons linéaires sont exactement les écritures où ρ parcourt , une fois ceci connu, l'ajustement requis des coefficients est atteint pour le seul choix de ρ = − Min_i(α_i) ; la troisième découle immédiatement de la seconde, puisqu'un hypothétique point de aurait deux écritures différentes vérifiant toutes les conditions ci-dessus).

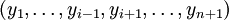
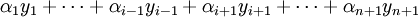
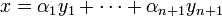
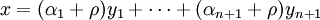
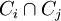
On peut alors entamer la démonstration proprement dite. Soit un point arbitraire de Conv(A), l'objectif étant de parvenir à l'écrire comme barycentre à coefficients positifs de n points de A ; quitte à prendre un système de coordonnées approprié sur l'espace affine ambiant, on peut supposer que celui-ci est et que le point étudié est l'origine. Le théorème de Carathéodory nous fournit déjà une écriture :

de 0 comme combinaison linéaire à coefficients positifs de n + 1 points de A.

Deux cas dégénérés se traitent sans difficulté : si un au moins des λ_i est nul, on a terminé ; si l'enveloppe affine des x_i n'est pas tout entier, en appliquant le théorème de Carathéodory dans cette enveloppe affine on peut diminuer d'au moins un le nombre de ceux-ci dans l'écriture de 0.

Reste le cas sérieux, celui où les x_i forment un repère affine de , tous les coefficients λ_i qui apparaissent dans (1) étant strictement positifs. On pose alors pour chaque indice i, y_i = − λ_ix_i : ces points sont positionnés comme sommets d'un simplexe dont le centre de gravité est à l'origine et on peut donc utiliser les C_i introduits en préliminaires.

Parmi les n + 1 points x_i de A, qui a au plus n composantes connexes, il est inévitable que deux au moins, disons x_j et x_k appartiennent à une même composante connexe A₀ de A. Cela entraîne que A ne peut être inclus dans  : si tel était le cas, la division de A₀ en les deux parties et découperait A₀ en deux ouverts (dans A₀) disjoints, non vides puisque l'un contient x_j et l'autre x_k. On a donc ainsi montré que A contient au moins un point x qui n'est dans aucun des C_i.

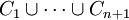
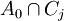
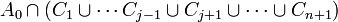
Vu d'une part la remarque (i), et vu d'autre part la non-appartenance de x aux C_i, c'est donc que x peut être écrit comme combinaison linéaire des y_i à coefficients tous positifs dont deux au moins sont nuls ; quitte à renuméroter les x_i, on supposera pour simplifier l'écriture que ce sont les deux premiers.

On dispose alors, pour ce point x de A d'une écriture :

dans laquelle tous les β_i sont positifs.

Il ne reste plus qu'à regrouper différemment celle-ci, en allant rechercher la définition des y_i :

pour obtenir ce qu'on cherchait depuis le début : une écriture de 0 comme barycentre à coefficients positifs de seulement n points de A.