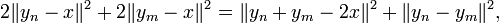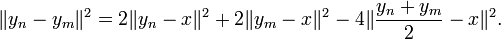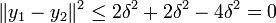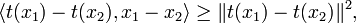Théorème de projection sur un convexe fermé - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance dont le principal corollaire est l'existence d'un supplémentaire orthogonal, donc d'une projection orthogonale sur un sous-espace vectoriel. Dans le cadre particulier d'un espace de Hilbert, il remplace avantageusement le théorème de Hahn-Banach. Il est en effet plus simple à démontrer et plus puissant dans ses conséquences.
Il possède de nombreuses applications, en analyse fonctionnelle, en algèbre linéaire, en théorie des jeux, pour la modélisation mathématiques des sciences économiques ou encore pour la programmation linéaire.
Énoncé du théorème
Dans cet article E désigne un espace préhilbertien réel, c'est-à-dire un espace vectoriel sur R muni d'un produit scalaire, x désigne un vecteur et C un ensemble convexe complet de E. La distance entre x et C désigne la borne inférieure des distances entre x et un point de C.
La version la plus générale du théorème est la suivante :
Théorème de la projection sur un convexe complet — Il existe une unique application t de E dans C, dite projection sur le convexe, qui à x associe le point t(x) de C, tel que la distance de x à C soit égale à celle de x à t(x). Le vecteur t(x) est l'unique point de C vérifiant les deux propositions suivantes, qui sont équivalentes :
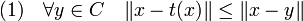
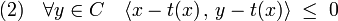
Dans le cas où l'espace E est de Hilbert, c'est-à-dire complet, supposer que C est complet équivaut à supposer qu'il est fermé. L'application t est parfois dénommée projecteur de meilleure approximation.
-
- Montrons l'existence de t(x) vérifiant (1) :
Soit δ la distance entre x et C, (yn) une suite de C tel que le carré de la distance entre x et yn soit inférieur ou égal à δ2 + 1/n. Soit n et m deux entiers, alors d'après l'identité du parallélogramme,
ce qui se réécrit :
En majorant les deux premiers termes du second membre de l'égalité et en remarquant que le milieu de yn et ym est un point de C donc à une distance supérieure ou égale à δ de x, on obtient :
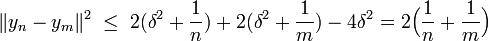
La dernière majoration établit le fait que la suite (yn) est de Cauchy donc convergente dans C qui est complet. La limite est un point de C, dont la distance à x est minimale.
-
- Montrons l'unicité de t(x) vérifiant (1) :
Soient y1 et y2 deux points de C à distance δ de x. Par le même calcul que ci-dessus,
donc y1=y2.
Rappelons les deux majorations du théorème.
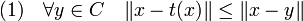
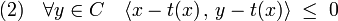
-
- Montrons que la propriété (1) implique (2) :
Soient y un élément de C et θ un réel compris entre 0 et 1, alors le barycentre θ y + (1 - θ) t(x), élément de C, est plus éloigné de x que t(x), d'après la propriété (1), donc :
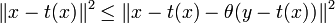
On en déduit la majoration :
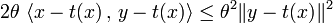
Il suffit alors de diviser par θ puis de passer à la limite quand θ tend vers 0 (par valeurs strictement positives) pour obtenir le résultat.
-
- Montrons que la propriété (2) implique (1) :
-
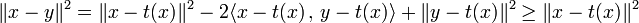
Remarquons qu'ici, la convexité de C n'est pas utile.
Elle possède de plus les propriétés suivantes :
Propriétés de la projection — La projection t est idempotente, c'est-à-dire que la composée de l'application t avec elle-même est égale à t ; elle est 1-lipschitzienne, c'est-à-dire que les images de deux points sont à une distance moindre que leurs antécédents ; enfin elle est monotone au sens suivant :
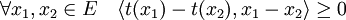
-
- L'application t est idempotente :
En effet, si x est un élément de E, t(x) est élément de convexe, son image est donc lui-même.
-
- L'application t est "monotone" :
C'est une conséquence directe du fait que <t(x1) - x1 , t(x1) - t(x2)> et <t(x2) - x2 , t(x2) - t(x1> sont tous deux négatifs ou nuls. En sommant ces deux inégalités on obtient que
qui est positif ou nul.
-
- L'application t est 1-lipschitzienne :
se déduit aussi de la minoration ci-dessus, grâce à l'inégalité de Cauchy-Schwarz.